13.4 课题学习 最短路径问题学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 13.4 课题学习 最短路径问题学案(要点讲解+当堂检测+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 10:46:18 | ||
图片预览


文档简介
人教版数学八年级上册同步学案
第十三章 轴对称
13.4 课题学习 最短路径问题
要 点 讲 解
要点 最短路径问题
1. 最短路径问题
(1)求直线异侧的两点到直线上一点距离的和最小的问题,只要连接这两点,所得线段与直线的交点即为所求的位置.
如图1所示,点A,B分别是直线l异侧的两个点,在l上找到一个点C,使CA+CB最小,这时点C是直线l与AB的交点.依据是两点之间线段最短.
图1 图2
(2)求直线同侧的两点到直线上一点距离的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,所得线段与该直线的交点即为所求的位置.
如图2所示,点A,B分别是直线l同侧的两个点,在l上找到一个点C,使CA+CB最小.这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点;或者先作点A关于直线l的对称点A′,则点C是直线l与A′B的交点,可以证明点C的位置符合要求.
证明:在直线l上另外任取一点C′,连接AC′,BC′,B′C′.
由作图可知,点B和点B′关于直线l对称,所以直线l是线段BB′的垂直平分线.因为点C与点C′在直线l上,所以BC=B′C,BC′=B′C′.在△AB′C′中,AB′<AC′+B′C′,所以AC+CB′<AC′+B′C′,所以AC+BC<AC′+BC′.
(3)求两相交线之间一点到两直线的距离
如图3,在直线l1,l2上分别求点M,N,使PM+MN+PN的长度之和最小.分别作点P关于两直线l1,l2的对称点P′,P″,连接P′P″与两直线的交点即为点M,N.PM+MN+PN的最小值为P′P″的值.
图3 图4
(4)求两相交线之间两点到两直线的距离的和最小的问题
如图4,在直线l1,l2上分别求点M,N,使PM+MN+NQ+PQ的长度之和最小.分别作点P,Q关于直线l1,l2的对称点P′,Q′,连接P′Q′,与两直线的交点即为点M,N.PM+MN+NQ+PQ的最小值为P′Q′+PQ的值.
经典例题1 如图所示,OX,OY是两条公路,在两条公路夹角的内部有一油库A,现在想在两条公路边分别建一个加油站,为使运油的油罐车从油库出发先到一个加油站,再到另一个加油站,最后回到油库的路程最短,问加油站应如何选址?请说明理由.
解:如图所示,分别作点A关于射线OX,OY的对称点A1,A2,连接A1A2交OX,OY于B,C两点,则B,C两点就是加油站的位置.
理由:设M,N(不同于为B,C)分别是射线OX,OY上的任意两点,连接A1M,MN,NA2,AB,AC,AM,AN.
因为点A,A1关于射线OX对称,所以A1B=AB,A1M=AM.
又因为点A,A2关于射线OY对称,所以AC=A2C,AN=A2N.
所以AB+BC+CA=A1B+BC+CA2=A1A2,AM+MN+AN=A1M+MN+A2N.
由“两点之间,线段最短”,可知A1M+MN+A2N>A1A2,所以B,C两点为加油站的位置.
2. “造桥选址问题”
解决“造桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
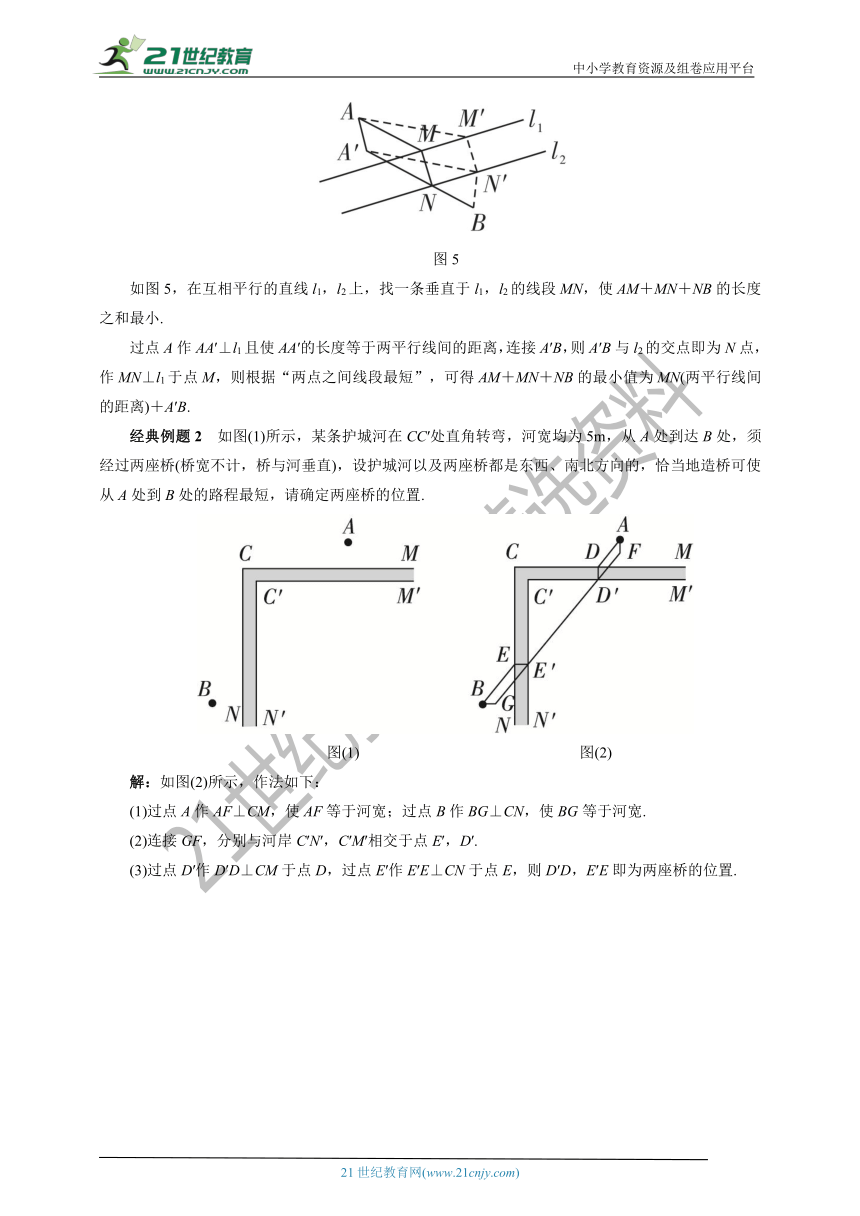
图5
如图5,在互相平行的直线l1,l2上,找一条垂直于l1,l2的线段MN,使AM+MN+NB的长度之和最小.
过点A作AA′⊥l1且使AA′的长度等于两平行线间的距离,连接A′B,则A′B与l2的交点即为N点,作MN⊥l1于点M,则根据“两点之间线段最短”,可得AM+MN+NB的最小值为MN(两平行线间的距离)+A′B.
经典例题2 如图(1)所示,某条护城河在CC′处直角转弯,河宽均为5m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A处到B处的路程最短,请确定两座桥的位置.
图(1) 图(2)
解:如图(2)所示,作法如下:
(1)过点A作AF⊥CM,使AF等于河宽;过点B作BG⊥CN,使BG等于河宽.
(2)连接GF,分别与河岸C′N′,C′M′相交于点E′,D′.
(3)过点D′作D′D⊥CM于点D,过点E′作E′E⊥CN于点E,则D′D,E′E即为两座桥的位置.
当 堂 检 测
1. 如图,直线l外有不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
A. 转化思想
B. 三角形的两边之和大于第三边
C. 两点之间,线段最短
D. 三角形的一个外角大于与它不相邻的任意一个内角
第1题 第2题
2. 如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A. (-2,0) B. (4,0) C. (2,0) D. (0,0)
3. 如图,在△ABC中,AB=3,AC=4,EF垂直平分BC,点P是直线EF上的任一点,则AP+BP的最小值是( )
A. 4 B. 5 C. 6 D. 7
第3题 第4题
4. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小时,∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
5. 从A到B有三条路径,选择路径 时,路程最短,理由是 .
6. 如图,某牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为500米.
(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水所走的路程最短?
(2)最短路程是多少?
7. 如图,已知在直线l的同侧有两点A,B.
(1)在图1的直线上找一点P,使PA+PB最短;
(2)在图2的直线上找一点P,使PA-PB最长.
当堂检测参考答案
1. D 2. C 3. A 4. B
5. ② 两点之间,线段最短
6. 解:(1)在CD的中点处饮水所走的路程最短.
(2)最短路程是1000米.
7. 解:(1)作点B关于直线l的对称点C,连接AC交直线l于点P,连接BP.点P即为所求.图略.
(2)连接AB并延长,交直线l于点P.点P即为所求.图略.
第十三章 轴对称
13.4 课题学习 最短路径问题
要 点 讲 解
要点 最短路径问题
1. 最短路径问题
(1)求直线异侧的两点到直线上一点距离的和最小的问题,只要连接这两点,所得线段与直线的交点即为所求的位置.
如图1所示,点A,B分别是直线l异侧的两个点,在l上找到一个点C,使CA+CB最小,这时点C是直线l与AB的交点.依据是两点之间线段最短.
图1 图2
(2)求直线同侧的两点到直线上一点距离的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,所得线段与该直线的交点即为所求的位置.
如图2所示,点A,B分别是直线l同侧的两个点,在l上找到一个点C,使CA+CB最小.这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点;或者先作点A关于直线l的对称点A′,则点C是直线l与A′B的交点,可以证明点C的位置符合要求.
证明:在直线l上另外任取一点C′,连接AC′,BC′,B′C′.
由作图可知,点B和点B′关于直线l对称,所以直线l是线段BB′的垂直平分线.因为点C与点C′在直线l上,所以BC=B′C,BC′=B′C′.在△AB′C′中,AB′<AC′+B′C′,所以AC+CB′<AC′+B′C′,所以AC+BC<AC′+BC′.
(3)求两相交线之间一点到两直线的距离
如图3,在直线l1,l2上分别求点M,N,使PM+MN+PN的长度之和最小.分别作点P关于两直线l1,l2的对称点P′,P″,连接P′P″与两直线的交点即为点M,N.PM+MN+PN的最小值为P′P″的值.
图3 图4
(4)求两相交线之间两点到两直线的距离的和最小的问题
如图4,在直线l1,l2上分别求点M,N,使PM+MN+NQ+PQ的长度之和最小.分别作点P,Q关于直线l1,l2的对称点P′,Q′,连接P′Q′,与两直线的交点即为点M,N.PM+MN+NQ+PQ的最小值为P′Q′+PQ的值.
经典例题1 如图所示,OX,OY是两条公路,在两条公路夹角的内部有一油库A,现在想在两条公路边分别建一个加油站,为使运油的油罐车从油库出发先到一个加油站,再到另一个加油站,最后回到油库的路程最短,问加油站应如何选址?请说明理由.
解:如图所示,分别作点A关于射线OX,OY的对称点A1,A2,连接A1A2交OX,OY于B,C两点,则B,C两点就是加油站的位置.
理由:设M,N(不同于为B,C)分别是射线OX,OY上的任意两点,连接A1M,MN,NA2,AB,AC,AM,AN.
因为点A,A1关于射线OX对称,所以A1B=AB,A1M=AM.
又因为点A,A2关于射线OY对称,所以AC=A2C,AN=A2N.
所以AB+BC+CA=A1B+BC+CA2=A1A2,AM+MN+AN=A1M+MN+A2N.
由“两点之间,线段最短”,可知A1M+MN+A2N>A1A2,所以B,C两点为加油站的位置.
2. “造桥选址问题”
解决“造桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
图5
如图5,在互相平行的直线l1,l2上,找一条垂直于l1,l2的线段MN,使AM+MN+NB的长度之和最小.
过点A作AA′⊥l1且使AA′的长度等于两平行线间的距离,连接A′B,则A′B与l2的交点即为N点,作MN⊥l1于点M,则根据“两点之间线段最短”,可得AM+MN+NB的最小值为MN(两平行线间的距离)+A′B.
经典例题2 如图(1)所示,某条护城河在CC′处直角转弯,河宽均为5m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A处到B处的路程最短,请确定两座桥的位置.
图(1) 图(2)
解:如图(2)所示,作法如下:
(1)过点A作AF⊥CM,使AF等于河宽;过点B作BG⊥CN,使BG等于河宽.
(2)连接GF,分别与河岸C′N′,C′M′相交于点E′,D′.
(3)过点D′作D′D⊥CM于点D,过点E′作E′E⊥CN于点E,则D′D,E′E即为两座桥的位置.
当 堂 检 测
1. 如图,直线l外有不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
A. 转化思想
B. 三角形的两边之和大于第三边
C. 两点之间,线段最短
D. 三角形的一个外角大于与它不相邻的任意一个内角
第1题 第2题
2. 如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A. (-2,0) B. (4,0) C. (2,0) D. (0,0)
3. 如图,在△ABC中,AB=3,AC=4,EF垂直平分BC,点P是直线EF上的任一点,则AP+BP的最小值是( )
A. 4 B. 5 C. 6 D. 7
第3题 第4题
4. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小时,∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
5. 从A到B有三条路径,选择路径 时,路程最短,理由是 .
6. 如图,某牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为500米.
(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水所走的路程最短?
(2)最短路程是多少?
7. 如图,已知在直线l的同侧有两点A,B.
(1)在图1的直线上找一点P,使PA+PB最短;
(2)在图2的直线上找一点P,使PA-PB最长.
当堂检测参考答案
1. D 2. C 3. A 4. B
5. ② 两点之间,线段最短
6. 解:(1)在CD的中点处饮水所走的路程最短.
(2)最短路程是1000米.
7. 解:(1)作点B关于直线l的对称点C,连接AC交直线l于点P,连接BP.点P即为所求.图略.
(2)连接AB并延长,交直线l于点P.点P即为所求.图略.
