2.5 从力做的功到向量的数量积 课件(26张PPT)
文档属性
| 名称 | 2.5 从力做的功到向量的数量积 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 00:00:00 | ||
图片预览








文档简介
课件26张PPT。 [创设情境、导入新课] 问题1:请同学们回顾一下,我们已经研究了向量的哪些运算?这些运算的结果是什么 ?
问题2:请同学们继续回忆,我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研究了这种运算的?
本节课我们仍然按照这种研究思路来研究向量的另外一种运算:平面向量的数量积运算
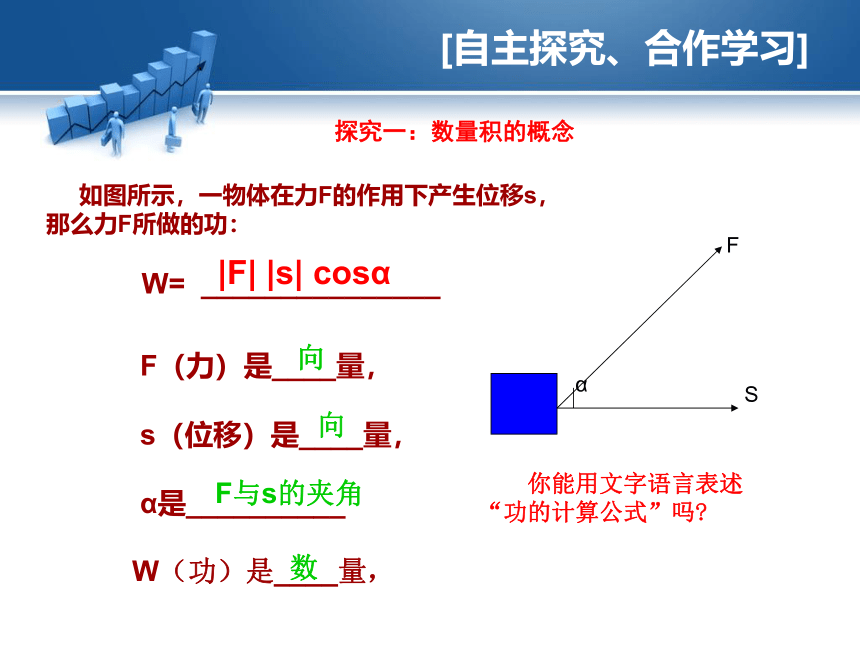
向量的加法、减法及数乘运算物理模型----概念---性质---应用 [自主探究、合作学习] 如图所示,一物体在力F的作用下产生位移s,
那么力F所做的功:
W= _______________
F(力)是____量,
s(位移)是____量,
α是__________
W(功)是____量,
|F| |s| cosα数向向F与s的夹角 探究一:数量积的概念 你能用文字语言表述“功的计算公式”吗? 我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念。2.5.1从力做的功到向量的数量积平面向量数量积的定义:注意: (1) 两个向量的数量积是一个实数,不是向量. (2)两个向量的数量积称为内积,写
成 .注意: (3) 向量的数量积和实数与向量的积(数乘)不是一回事. 数量积 的结果是一个数量(实数);实数与向量的积(数乘)还是一个向量.[自主探究、合作学习]①其中一个向量是零向量数量积是多少?
②数量积是数量还是向量?
③数量积的符号和大小受哪些因素的影响?
特别地:零向量与任一向量的数量积为0.
两个非零向量 和 ,作 , ,则
( )叫作向量 与 的夹角.思考1 如何定义向量的夹角?计算向量的夹角时要将两个向量起点放在一起.探究点1 向量的数量积θ为锐角有时也记作《 , 》向量的夹角记作θ为钝角均为非零向量[自主探究、合作学习]判断下列结论是否正确: (1) (2) (3) (4)[自主探究、合作学习] 探究二:研究数量积的几何意义 1.向量投影的概念: 如图,我们把_________________ 叫做
向量 在 方向上的投影。投影是个数量,一定大于零吗? 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:[自主探究、合作学习]数量积的几何意义是什么?平面向量数量积的几何意义:[自主探究、合作学习] 探究三:探究数量积的运算性质 数量积的性质
性质:若 和 均为非零向量
(1) _________(垂直)
(2) ______________ ,
______________
特别地: = _________= _________(长度)
(3)cosθ= (夹角)
(4) (4)的关系是什么?
何时取等号?当且仅当 ∥ 时等号成立特别提醒:
1.
2.若 是单位向量,则3.若 是单位向量,则:求向量的数量积及向量的模 例1. 已知|a|=3,|b|=4且a与b的夹角为θ=120°,求:a·b,(a+b) 2,|a-b|.分析:根据向量的运算律求(a+b)2,|a-b|,求模时转化为求向量的平方问题,即|a|2=a2.点评: 利用|a|2=a2求向量的模时转化为求向量的平方问题.4.例题剖析 加强应用题型一600[反馈训练、巩固落实]充充电吧![归纳总结、提升拓展] 知识:
(1)平面向量的数量积;
(2)平面向量的数量积的几何意义;
(3)平面向量数量积的重要性质
思想方法:
(1)转化、数形结合、分类讨论等思想
(2)公式或定义法谢谢!
问题2:请同学们继续回忆,我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研究了这种运算的?
本节课我们仍然按照这种研究思路来研究向量的另外一种运算:平面向量的数量积运算
向量的加法、减法及数乘运算物理模型----概念---性质---应用 [自主探究、合作学习] 如图所示,一物体在力F的作用下产生位移s,
那么力F所做的功:
W= _______________
F(力)是____量,
s(位移)是____量,
α是__________
W(功)是____量,
|F| |s| cosα数向向F与s的夹角 探究一:数量积的概念 你能用文字语言表述“功的计算公式”吗? 我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念。2.5.1从力做的功到向量的数量积平面向量数量积的定义:注意: (1) 两个向量的数量积是一个实数,不是向量. (2)两个向量的数量积称为内积,写
成 .注意: (3) 向量的数量积和实数与向量的积(数乘)不是一回事. 数量积 的结果是一个数量(实数);实数与向量的积(数乘)还是一个向量.[自主探究、合作学习]①其中一个向量是零向量数量积是多少?
②数量积是数量还是向量?
③数量积的符号和大小受哪些因素的影响?
特别地:零向量与任一向量的数量积为0.
两个非零向量 和 ,作 , ,则
( )叫作向量 与 的夹角.思考1 如何定义向量的夹角?计算向量的夹角时要将两个向量起点放在一起.探究点1 向量的数量积θ为锐角有时也记作《 , 》向量的夹角记作θ为钝角均为非零向量[自主探究、合作学习]判断下列结论是否正确: (1) (2) (3) (4)[自主探究、合作学习] 探究二:研究数量积的几何意义 1.向量投影的概念: 如图,我们把_________________ 叫做
向量 在 方向上的投影。投影是个数量,一定大于零吗? 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:[自主探究、合作学习]数量积的几何意义是什么?平面向量数量积的几何意义:[自主探究、合作学习] 探究三:探究数量积的运算性质 数量积的性质
性质:若 和 均为非零向量
(1) _________(垂直)
(2) ______________ ,
______________
特别地: = _________= _________(长度)
(3)cosθ= (夹角)
(4) (4)的关系是什么?
何时取等号?当且仅当 ∥ 时等号成立特别提醒:
1.
2.若 是单位向量,则3.若 是单位向量,则:求向量的数量积及向量的模 例1. 已知|a|=3,|b|=4且a与b的夹角为θ=120°,求:a·b,(a+b) 2,|a-b|.分析:根据向量的运算律求(a+b)2,|a-b|,求模时转化为求向量的平方问题,即|a|2=a2.点评: 利用|a|2=a2求向量的模时转化为求向量的平方问题.4.例题剖析 加强应用题型一600[反馈训练、巩固落实]充充电吧![归纳总结、提升拓展] 知识:
(1)平面向量的数量积;
(2)平面向量的数量积的几何意义;
(3)平面向量数量积的重要性质
思想方法:
(1)转化、数形结合、分类讨论等思想
(2)公式或定义法谢谢!
