1.8 函数y=Asin(ωx+ψ)的图像 课件(21张PPT)
文档属性
| 名称 | 1.8 函数y=Asin(ωx+ψ)的图像 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 369.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:31:12 | ||
图片预览







文档简介
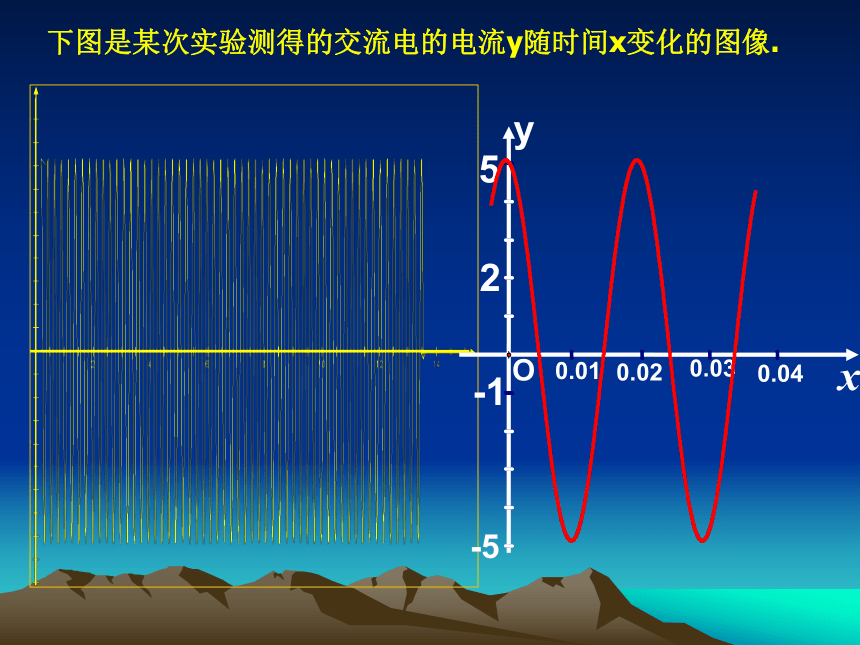
课件21张PPT。函数 的图像普通高中课程标准实验教科书数学(必修4)(第一课时)下图是某次实验测得的交流电的电流y随时间x变化的图像.
函数y=Asin(ωx +φ)的图像与参数A、 ω、φ的关系又是怎样的?如何由函数y=sinx 的图像经过变换得到函数y=Asin(ωx +φ)的图像?提出问题如何由y=sinx 的图像得到y=sin(x+φ) 的图像?
如何由y=sinx 的图像得到y=Asinx 的图像?
如何由y=sinx 的图像得到y=sinωx 的图像?
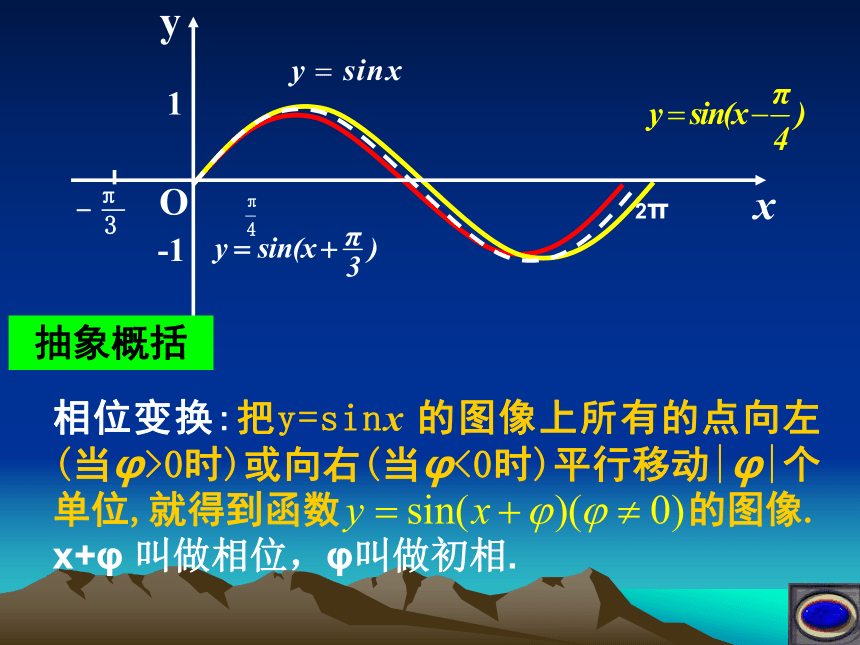
如何由y=sinx 的图像得到y=Asin(ωx+φ) 的图像?可以将上述问题分解为以下几个步骤来进行:分析问题一、探索φ对y=sin(x+φ)的图像的影响新知探究左左右右相位变换:把y=sinx 的图像上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位,就得到函数 的图像.
x+φ 叫做相位,φ叫做初相.
抽象概括新知探究二、探索A对 y=Asinx 的图像的影响抽象概括振幅变换:一般地,函数 的图像可以看作是把y=sinx图像上所有点的纵坐标伸长(当A>1时)或缩短(当0新知探究三、探索ω对y=sinωx的图像的影响探究活动三: 画出函数 和 的简图,并说明它们与函数 的关系.
抽象概括 一般地,函数y=sinωx的图像,可以看作是把y=sinx 的图像上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω倍(纵坐标不变)而得到的.周期变换:ω引起图像的横向伸缩.它决定函数的周期T=2π/ω.解答1(相位变换)所有点向左平移 个单位各点横坐标缩短到原来的 倍(周期变换)各点纵坐标伸长到原来的 倍(振幅变换)3四、探索y=Asin(ωx+φ)和y=sinx的图像关系探究活动四:如何由y=sinx的图像得到 的图像.解答2(相位变换)所有点向左平移 个单位各点横坐标缩短到原来的 倍(周期变换)各点纵坐标伸长到原来的 倍(振幅变换)3方法1:先平移后伸缩一般规律(2)向左(? >0)或向右(? <0)
平移| |个单位
方法2:先伸缩后平移一般规律1.函数y= sin(2x+ )的图像可以看作是把 函数y= sin2x的图像作以下平移( )A.向左平移 B.向右平移
C.向左平移 D.向右平移练一练及时反馈AD2.把 的图像向右平移 个单位,这时图像所对应的函数解析式为( )练一练(1) 在这节课学习后,你有什么收获?(2)你最感兴趣的是什么?(3)你想继续探究些什么?课堂小结利用“图像变换法”作函数y=Asin(?x+?) 的图像的方法.数形结合 化归转化 分类讨论
课堂小结1.基本知识:
2.思想方法:步骤1步骤2步骤3步骤4xyo-11yy(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)y=sinx
课堂小结作业:P.54 3(2)(3)布置作业课堂练习:P52 第2,3题再见
函数y=Asin(ωx +φ)的图像与参数A、 ω、φ的关系又是怎样的?如何由函数y=sinx 的图像经过变换得到函数y=Asin(ωx +φ)的图像?提出问题如何由y=sinx 的图像得到y=sin(x+φ) 的图像?
如何由y=sinx 的图像得到y=Asinx 的图像?
如何由y=sinx 的图像得到y=sinωx 的图像?
如何由y=sinx 的图像得到y=Asin(ωx+φ) 的图像?可以将上述问题分解为以下几个步骤来进行:分析问题一、探索φ对y=sin(x+φ)的图像的影响新知探究左左右右相位变换:把y=sinx 的图像上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位,就得到函数 的图像.
x+φ 叫做相位,φ叫做初相.
抽象概括新知探究二、探索A对 y=Asinx 的图像的影响抽象概括振幅变换:一般地,函数 的图像可以看作是把y=sinx图像上所有点的纵坐标伸长(当A>1时)或缩短(当0
抽象概括 一般地,函数y=sinωx的图像,可以看作是把y=sinx 的图像上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω倍(纵坐标不变)而得到的.周期变换:ω引起图像的横向伸缩.它决定函数的周期T=2π/ω.解答1(相位变换)所有点向左平移 个单位各点横坐标缩短到原来的 倍(周期变换)各点纵坐标伸长到原来的 倍(振幅变换)3四、探索y=Asin(ωx+φ)和y=sinx的图像关系探究活动四:如何由y=sinx的图像得到 的图像.解答2(相位变换)所有点向左平移 个单位各点横坐标缩短到原来的 倍(周期变换)各点纵坐标伸长到原来的 倍(振幅变换)3方法1:先平移后伸缩一般规律(2)向左(? >0)或向右(? <0)
平移| |个单位
方法2:先伸缩后平移一般规律1.函数y= sin(2x+ )的图像可以看作是把 函数y= sin2x的图像作以下平移( )A.向左平移 B.向右平移
C.向左平移 D.向右平移练一练及时反馈AD2.把 的图像向右平移 个单位,这时图像所对应的函数解析式为( )练一练(1) 在这节课学习后,你有什么收获?(2)你最感兴趣的是什么?(3)你想继续探究些什么?课堂小结利用“图像变换法”作函数y=Asin(?x+?) 的图像的方法.数形结合 化归转化 分类讨论
课堂小结1.基本知识:
2.思想方法:步骤1步骤2步骤3步骤4xyo-11yy(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)y=sinx
课堂小结作业:P.54 3(2)(3)布置作业课堂练习:P52 第2,3题再见
