1.1数列的概念 课件(32张PPT)
图片预览











文档简介
课件32张PPT。《数列的概念》(一)情景引入 理解定义《达芬奇密码》馆长索尼埃提示13,3,2,21,1,1,8,5
O,Draconiandevil!
啊,严酷的魔王!
Oh,Lame Saint!
噢,瘸腿的圣徒!(一)情境引入 理解定义13,3,2,21,1,1,8,5索尼埃密码1,1,2,3,5,8,13,21破译后明文
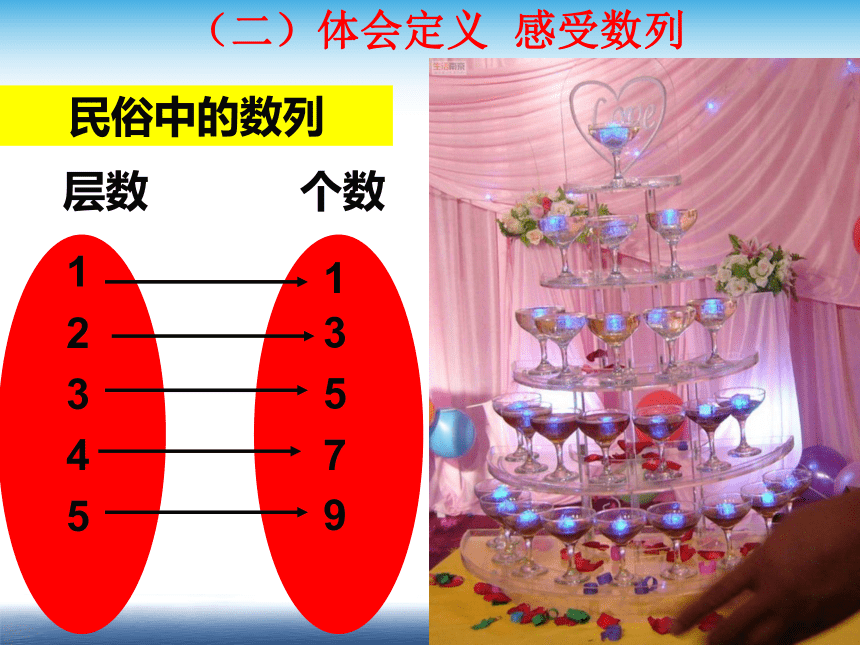
(斐波拉契数列)数列的定义按照一定顺序排列着的一列数,叫做数列.(一)情境引入 理解定义数列具有有序性(二)体会定义 感受数列自然中的数列(2)刺梅(二)体会定义 感受数列自然中的数列(3)(二)体会定义 感受数列自然中的数列(5)(二)体会定义 感受数列自然中的数列(8)刺梅(2)紫露草丁香花波斯菊瓜叶菊(3)(5)(8)(13)(二)体会定义 感受数列自然中的数列哈雷慧星回归周期为76年:2062天文中的数列(二)体会定义 感受数列1682,1758,1834,1910,1986,( )民俗中的数列12543(二)体会定义 感受数列个数层数
拉面在制作过程中由两根依次变为:
284321664(二)体会定义 感受数列生活中的数列曰:“一尺之棰,日取其半,万世不竭.”庄 子你能用一个数列来表达这句话的含义吗?(二)体会定义 感受数列文化中的数列51616283251 韩国
汉 城 西班牙
巴塞罗那 美国
亚特兰大澳大利亚
悉尼希腊
雅典 中国
北京我国奥运健儿从88年洛杉矶奥
运会到16年里约奥运会金牌数 英国
伦敦38体育中的数列(二)体会定义 感受数列巴西
里约26你能举出我们日常生活中的数列吗?各项依次叫做这个数列的第1项,第2项,··· ,第n项,···2、数列中的每个数叫
做这个数列的项.3、数列的分类按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列4. 数列的一般形式可以写成:????第1项第2项第3项第n项与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式.列的第1项或称为首项,?思考:解:思 考通项公式的作用?显然,有了通项公式,只要
依次用1,2,3,…代替公式
中的n,就可以求出这个数列的各项设某一数列的通项公式为20以内的正奇数按从小到大的顺序构成的数列也就是说每个序号也都
对应着一个数(项)序号项从函数的观点看,
是 的函数。 ann函数值自变量数列项序号(正整数或它的有限子集)项6、数列的实质序号项即,数列可以看成以正整数集(或它的有限子集{1,2,…,n})为定义域的函数,当自变量从小到大的顺序依次取值时,所对应的一列函数值。序号通项公式从映射的观点看,数列可以看作是:序号到数列项的映射·····数列用图象表示时的特点——一群孤立的点·····分析:解:这个数列的前4项的分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是分析:解:这个数列的奇数项是0,偶数项是2,所以它的一个通项公式是关于数列的通项公式的几点说明:(四)本质引领 实际运用(第一关)观察规律填空:(1)1,4 ,9 , ,25161529正方形数三角形数卢卡斯数第二关:第4个图案中绿色小三角形
的个数为_____。(四)本质引领 实际运用27谢宾斯基三角形(3)你能写出这个数列的通项公式吗?
9,99,999,9999,……(四)本质引领 实际运用(4)4是该数列的第 项?
(四)本质引领 实际运用4
本节课学习的主要内容有:1.数列的有关概念;2.数列的通项公式;3.数列的实质; 4.本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2) 会用观察法由数列的前几项求
数列的通项公式.作业: 课外探究
(1)选取某家银行实际考察存款方式,了解各种存款利息的计算原理。思考各种计算方式得出的数列是否是本章的数列模型。
(2)搜集生活中关于数列的实际模型,是否有符合本章的数列模型。
O,Draconiandevil!
啊,严酷的魔王!
Oh,Lame Saint!
噢,瘸腿的圣徒!(一)情境引入 理解定义13,3,2,21,1,1,8,5索尼埃密码1,1,2,3,5,8,13,21破译后明文
(斐波拉契数列)数列的定义按照一定顺序排列着的一列数,叫做数列.(一)情境引入 理解定义数列具有有序性(二)体会定义 感受数列自然中的数列(2)刺梅(二)体会定义 感受数列自然中的数列(3)(二)体会定义 感受数列自然中的数列(5)(二)体会定义 感受数列自然中的数列(8)刺梅(2)紫露草丁香花波斯菊瓜叶菊(3)(5)(8)(13)(二)体会定义 感受数列自然中的数列哈雷慧星回归周期为76年:2062天文中的数列(二)体会定义 感受数列1682,1758,1834,1910,1986,( )民俗中的数列12543(二)体会定义 感受数列个数层数
拉面在制作过程中由两根依次变为:
284321664(二)体会定义 感受数列生活中的数列曰:“一尺之棰,日取其半,万世不竭.”庄 子你能用一个数列来表达这句话的含义吗?(二)体会定义 感受数列文化中的数列51616283251 韩国
汉 城 西班牙
巴塞罗那 美国
亚特兰大澳大利亚
悉尼希腊
雅典 中国
北京我国奥运健儿从88年洛杉矶奥
运会到16年里约奥运会金牌数 英国
伦敦38体育中的数列(二)体会定义 感受数列巴西
里约26你能举出我们日常生活中的数列吗?各项依次叫做这个数列的第1项,第2项,··· ,第n项,···2、数列中的每个数叫
做这个数列的项.3、数列的分类按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列4. 数列的一般形式可以写成:????第1项第2项第3项第n项与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式.列的第1项或称为首项,?思考:解:思 考通项公式的作用?显然,有了通项公式,只要
依次用1,2,3,…代替公式
中的n,就可以求出这个数列的各项设某一数列的通项公式为20以内的正奇数按从小到大的顺序构成的数列也就是说每个序号也都
对应着一个数(项)序号项从函数的观点看,
是 的函数。 ann函数值自变量数列项序号(正整数或它的有限子集)项6、数列的实质序号项即,数列可以看成以正整数集(或它的有限子集{1,2,…,n})为定义域的函数,当自变量从小到大的顺序依次取值时,所对应的一列函数值。序号通项公式从映射的观点看,数列可以看作是:序号到数列项的映射·····数列用图象表示时的特点——一群孤立的点·····分析:解:这个数列的前4项的分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是分析:解:这个数列的奇数项是0,偶数项是2,所以它的一个通项公式是关于数列的通项公式的几点说明:(四)本质引领 实际运用(第一关)观察规律填空:(1)1,4 ,9 , ,25161529正方形数三角形数卢卡斯数第二关:第4个图案中绿色小三角形
的个数为_____。(四)本质引领 实际运用27谢宾斯基三角形(3)你能写出这个数列的通项公式吗?
9,99,999,9999,……(四)本质引领 实际运用(4)4是该数列的第 项?
(四)本质引领 实际运用4
本节课学习的主要内容有:1.数列的有关概念;2.数列的通项公式;3.数列的实质; 4.本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2) 会用观察法由数列的前几项求
数列的通项公式.作业: 课外探究
(1)选取某家银行实际考察存款方式,了解各种存款利息的计算原理。思考各种计算方式得出的数列是否是本章的数列模型。
(2)搜集生活中关于数列的实际模型,是否有符合本章的数列模型。
