4.2简单线性规划 课件(21张PPT)
文档属性
| 名称 | 4.2简单线性规划 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:29:28 | ||
图片预览




文档简介
课件21张PPT。学习数学知识
感受数学方法
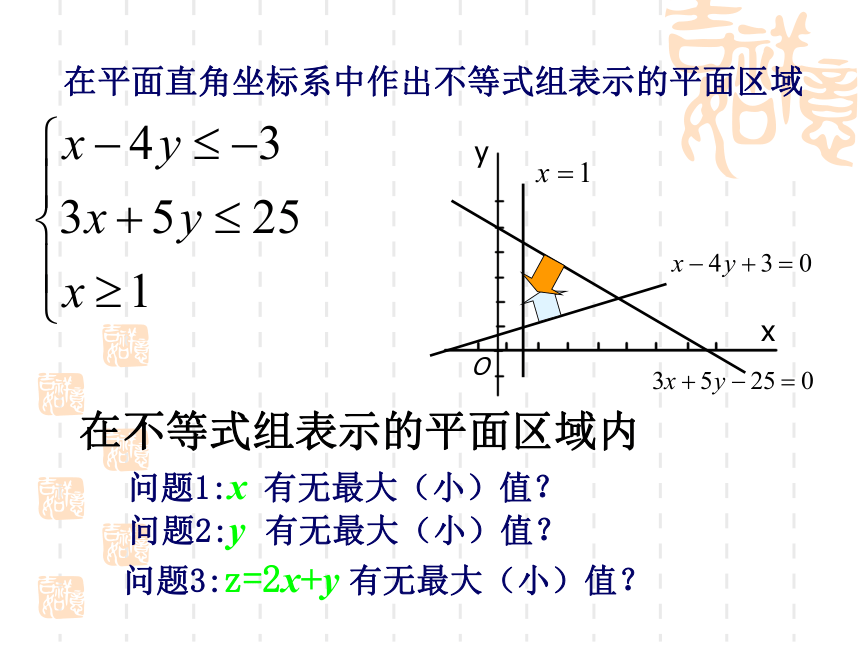
感悟数学思想 二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。 确定步骤: 若C≠0,则直线定界,原点定域;直线定界,特殊点定域;复习应该注意的几个问题:1、若不等式中是严格不等号(即不含0),
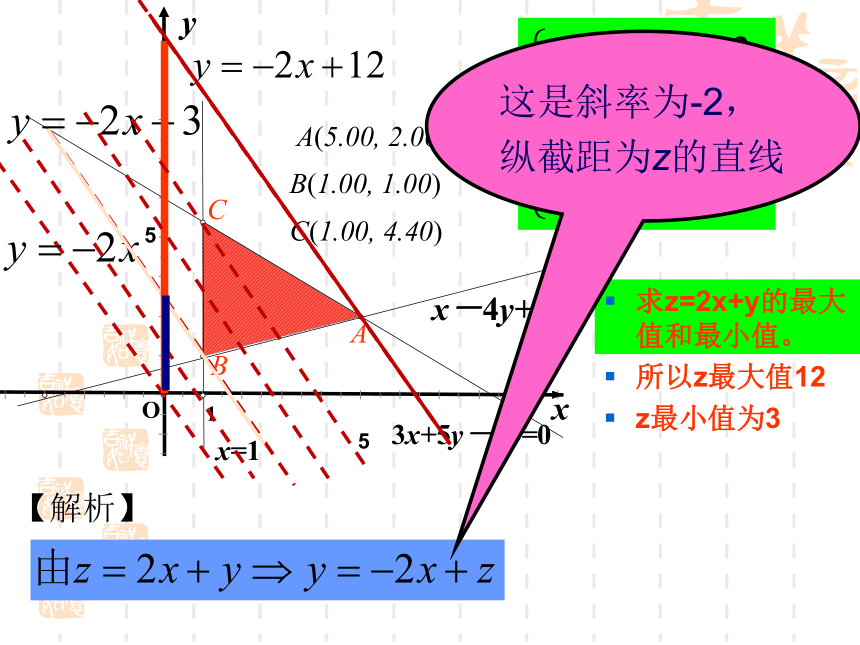
则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。 否则(即不等式中是非严格不等号时)应画成实线。yxO问题1:x 有无最大(小)值?问题2:y 有无最大(小)值?问题3:z=2x+y 有无最大(小)值?在不等式组表示的平面区域内在平面直角坐标系中作出不等式组表示的平面区域求z=2x+y的最大值和最小值。
所以z最大值12
z最小值为3
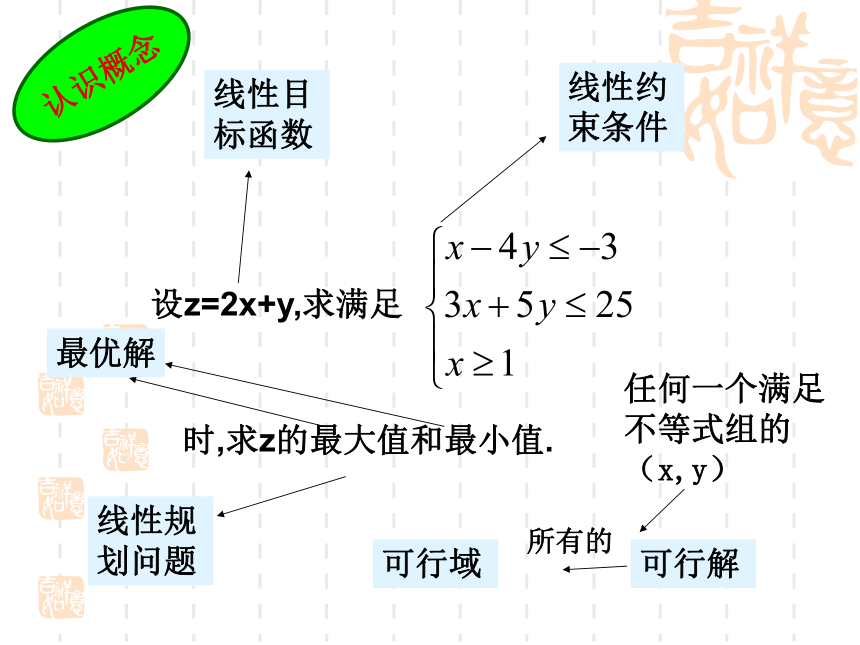
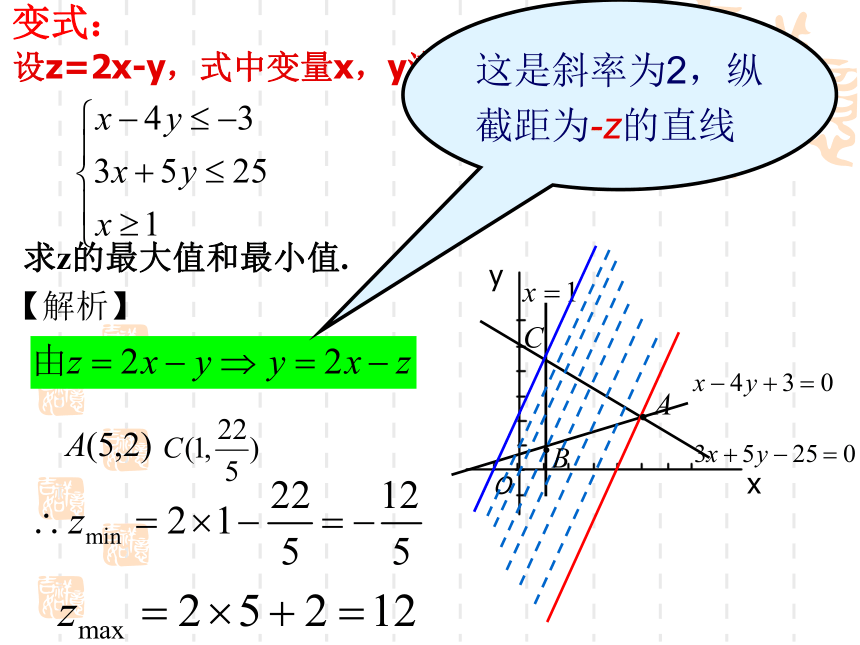
这是斜率为-2,纵截距为z的直线【解析】线性目标函数线性约束条件线性规划问题任何一个满足不等式组的(x,y)可行解可行域所有的最优解认识概念线性规划有关概念由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解。简单线性规划变式: 设z=2x-y,式中变量x,y满足下列条件求z的最大值和最小值.xyO这是斜率为2,纵截距为-z的直线【解析】解线性规划问题的步骤: (3)求:通过解方程组求出取得最大值或者最小值的点的坐标及最大值和最小值; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域,
和直线 不全为 目标函数为(2)移:平行移动直线 , 确定使
取得最大值和最小值的点;3求2移1画0xyx+y+5=0x-y=0Ax+y+5≥0y≤0例1.求z=2x+4y的最大值和最小值,x,y满足约束条件【解】(B)4答2x+4y=0两个结论:2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义y前系数为正y前系数为负1、线性目标函数的最大(小)值一般在可
行域的顶点处取得,也可能在边界处取得。 例2.营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪。1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元。
假如你是一个主妇你会如何合理的购买食用食物A和食物B多少kg呢? 运用新知解决问题 P103 : 1 ,2,求z=3x+5y的最大值和最小值,
使式中的x,y满足以下不等式组【解析】解线性规划问题的步骤:
通过本节课,你有什么收获? 小结(1)画:画出可行域;(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 学习数学知识
感受数学方法
感悟数学思想思维升华线性规划及其相关概念图解法解线性规划问题数形结合及化归的思想
必做题: 完成例2的解答过程
习题3-4 A组第4题
选做题:108页A组第3题
已知
求z=3x+5y的最大值和最小值。高考怎样考
(浙江高考)551Oxy1-15x+3y=15X-5y=3y=x+1A(-2,-1)B(3/2,5/2)
感受数学方法
感悟数学思想 二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。 确定步骤: 若C≠0,则直线定界,原点定域;直线定界,特殊点定域;复习应该注意的几个问题:1、若不等式中是严格不等号(即不含0),
则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。 否则(即不等式中是非严格不等号时)应画成实线。yxO问题1:x 有无最大(小)值?问题2:y 有无最大(小)值?问题3:z=2x+y 有无最大(小)值?在不等式组表示的平面区域内在平面直角坐标系中作出不等式组表示的平面区域求z=2x+y的最大值和最小值。
所以z最大值12
z最小值为3
这是斜率为-2,纵截距为z的直线【解析】线性目标函数线性约束条件线性规划问题任何一个满足不等式组的(x,y)可行解可行域所有的最优解认识概念线性规划有关概念由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解。简单线性规划变式: 设z=2x-y,式中变量x,y满足下列条件求z的最大值和最小值.xyO这是斜率为2,纵截距为-z的直线【解析】解线性规划问题的步骤: (3)求:通过解方程组求出取得最大值或者最小值的点的坐标及最大值和最小值; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域,
和直线 不全为 目标函数为(2)移:平行移动直线 , 确定使
取得最大值和最小值的点;3求2移1画0xyx+y+5=0x-y=0Ax+y+5≥0y≤0例1.求z=2x+4y的最大值和最小值,x,y满足约束条件【解】(B)4答2x+4y=0两个结论:2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义y前系数为正y前系数为负1、线性目标函数的最大(小)值一般在可
行域的顶点处取得,也可能在边界处取得。 例2.营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪。1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元。
假如你是一个主妇你会如何合理的购买食用食物A和食物B多少kg呢? 运用新知解决问题 P103 : 1 ,2,求z=3x+5y的最大值和最小值,
使式中的x,y满足以下不等式组【解析】解线性规划问题的步骤:
通过本节课,你有什么收获? 小结(1)画:画出可行域;(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 学习数学知识
感受数学方法
感悟数学思想思维升华线性规划及其相关概念图解法解线性规划问题数形结合及化归的思想
必做题: 完成例2的解答过程
习题3-4 A组第4题
选做题:108页A组第3题
已知
求z=3x+5y的最大值和最小值。高考怎样考
(浙江高考)551Oxy1-15x+3y=15X-5y=3y=x+1A(-2,-1)B(3/2,5/2)
