人教版八年级数学上册第十一章三角形章末复习课件(共70张)
文档属性
| 名称 | 人教版八年级数学上册第十一章三角形章末复习课件(共70张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-01 08:20:19 | ||
图片预览





文档简介
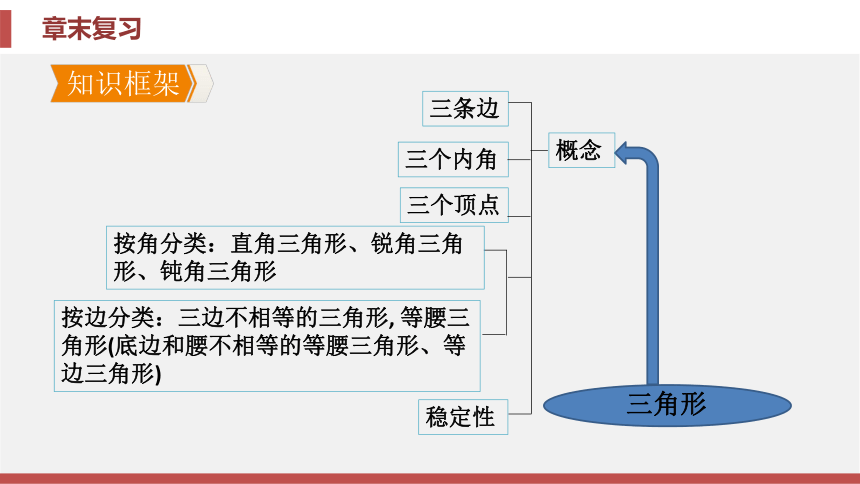
课件70张PPT。八年级 上册新课标(RJ)数 学 第十一章 三角形章末复习第十一章 三角形章末复习概念三条边三个内角三个顶点稳定性按角分类:直角三角形、锐角三角形、钝角三角形按边分类:三边不相等的三角形, 等腰三角形(底边和腰不相等的等腰三角形、等边三角形)与三角形
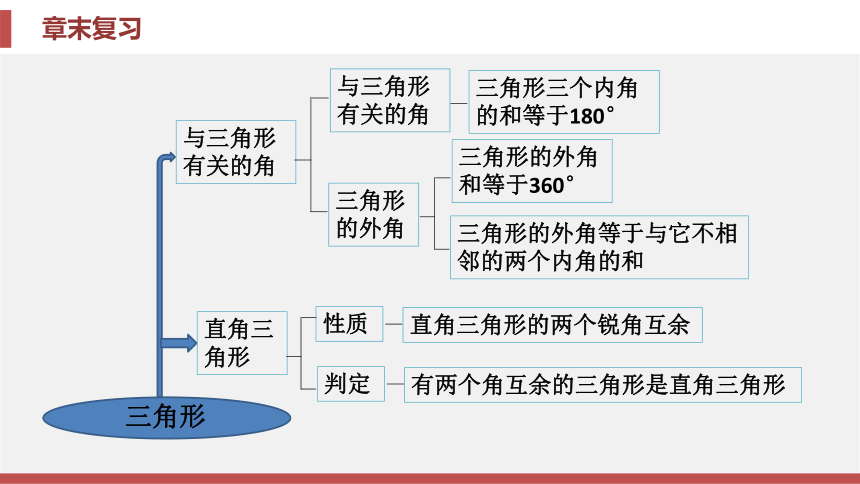
有关的角与三角形
有关的角三角形三个内角的和等于180°三角形
的外角三角形的外角
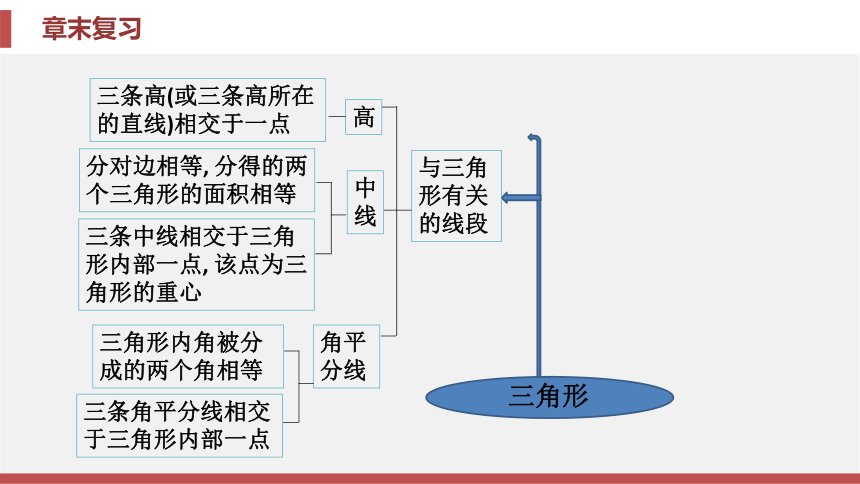
和等于360°三角形的外角等于与它不相邻的两个内角的和直角三角形性质直角三角形的两个锐角互余判定有两个角互余的三角形是直角三角形与三角形有关的线段高中
线角平分线三条高(或三条高所在的直线)相交于一点分对边相等, 分得的两
个三角形的面积相等三条中线相交于三角形内部一点, 该点为三角形的重心三角形内角被分
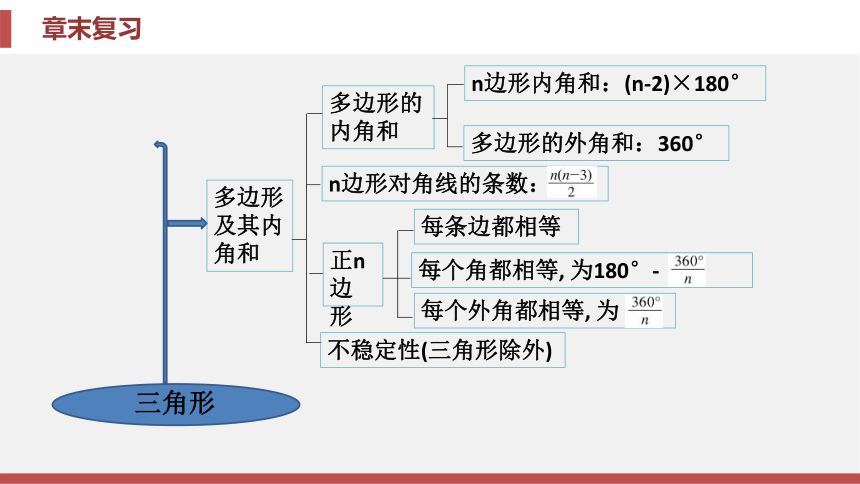
成的两个角相等三条角平分线相交于三角形内部一点多边形及其内角和多边形的内角和n边形内角和:(n-2)×180°多边形的外角和:360°n边形对角线的条数:正n
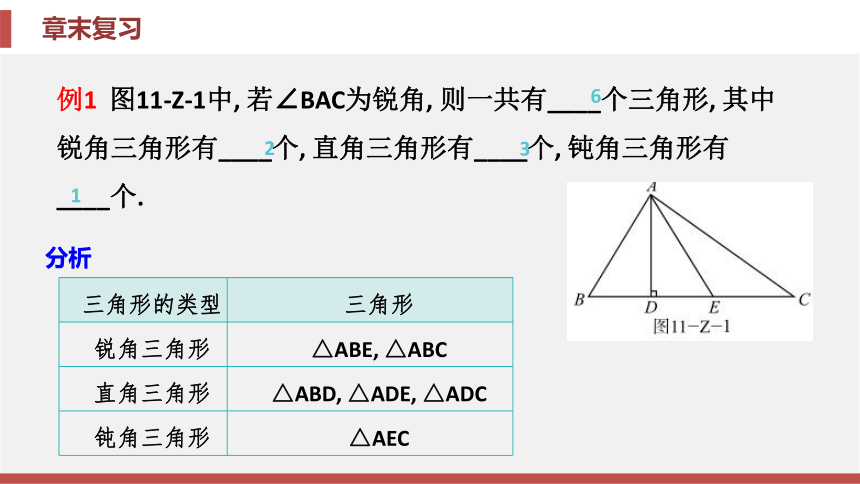
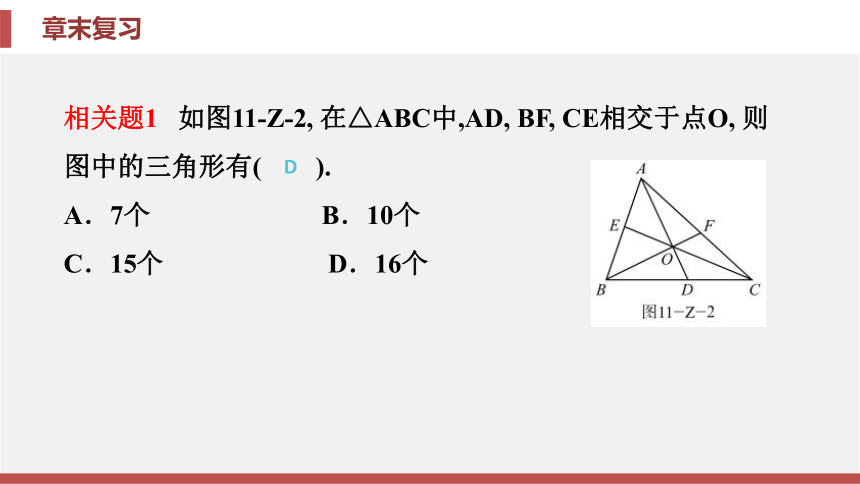
边形不稳定性(三角形除外)每条边都相等每个角都相等, 为180°-每个外角都相等, 为【要点指导】确定一个图形中三角形的个数时, 应用分类讨论思想和枚举法按照一定的规律来计数, 如按照不同的边或顶点来寻找.专题一 三角形的计数例1 图11-Z-1中, 若∠BAC为锐角, 则一共有____个三角形, 其中锐角三角形有____个, 直角三角形有____个, 钝角三角形有____个. 623 1分析 相关题1 如图11-Z-2, 在△ABC中,AD, BF, CE相交于点O, 则图中的三角形有( ).
A.7个 B.10个
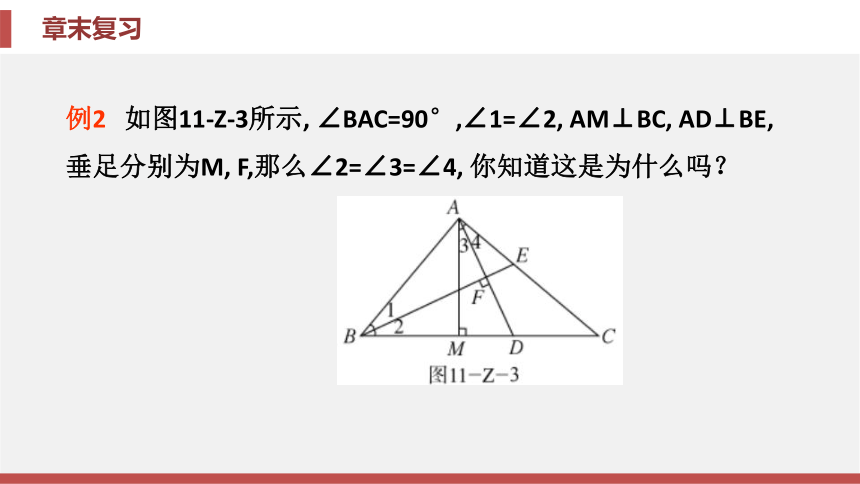
C.15个 D.16个D【要点指导】“直角三角形的两锐角互余”是直角三角形的性质;“有两个角互余的三角形是直角三角形”是直角三角形的判定. 在运用直角三角形的性质和判定的过程中, 常与三角形的角平分线、高等结合在一起.专题二 直角三角形的有关计算例2 如图11-Z-3所示, ∠BAC=90°,∠1=∠2, AM⊥BC, AD⊥BE, 垂足分别为M, F,那么∠2=∠3=∠4, 你知道这是为什么吗?解 在Rt△BDF与Rt△ADM中,
∵∠2+∠ADB=90°, ∠3+∠ADB=90°,
∴∠2=∠3.
在Rt△ABE与Rt△AEF中,
∵∠1+∠AEB=90°, ∠4+∠AEB=90°,
∴∠1=∠4.
又∵∠1=∠2, ∴∠2=∠3=∠4.相关题2-1 如图11-Z-4, Rt△ABC的两个锐角的平分线AE,BD所夹的锐角∠AOD是( ).
A.30° B.60°
C.45° D.15°或75°C相关题2-2 如图11-Z-5所示, 已知在△ABC中, ∠ACB=90°,CD为AB边上的高, ∠ABC的平分线BE与CD, CA分别交于点F, E, 则下列结论正确的是( ).
①∠CFE=∠CEF; ②∠FCB=∠FBC;
③∠A=∠DCB;
④∠CFE与∠CBF互余.
A.①③④ B.②③④
C.①②④ D.①②③A【要点指导】三角形任意两边之和大于第三边, 任意两边之差小于
第三边, 这两种关系可用一句话来概括:设三角形的三边长分别为a, b, c,则|b-c|(b-2)2=0,|c-3|=0,
解得b=2,c=3.
由方程|x-4|=2,得x-4=2或x-4=-2,
∴x=6或x=2,即a=6或a=2.当a=6时,2+3<6,不能组成三角形,故舍去;
当a=2时,2+2>3,能组成三角形,
∴a=2,b=2,c=3.
∵2+2+3=7,
∴△ABC的周长为7.专题四 复杂图形中角度的计算【要点指导】求复杂图形中的角度时, 常利用转化的思想将分散的角转化到一个多边形中, 再利用多边形的内角和与外角和来解答.例4 [泰安中考]如图11-Z-6, 求∠A+∠B+∠BCD+∠D+∠E+ ∠EFG+∠G的度数.相关题4 如图11-Z-7所示, ∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )度.
A.450 B.540
C.630 D.720B专题五 三角形内角和定理与外角的性质【要点指导】三角形内角和定理与外角的性质是求解与角有关问题的主要依据, 是中考的热点内容, 在中考题中主要以填空题、选择题的形式出现, 解答题中也常用到一些有关的知识.例5 [泰安中考]如图11-Z-8, 在△ABC中, D是BC边上一点,
∠1=∠2, ∠3=∠4, ∠BAC=63°, 求∠DAC的度数.解 设∠1=∠2=x, 则∠3=∠4=2x.
∵∠BAC=63°, ∴∠2+∠4=117°,
即x+2x=117°, 解得x=39°,
∴∠3=∠4=78°,
∴∠DAC=180°-∠3-∠4=24°.相关题5 如图11-Z-9, BP是△ABC中∠ABC的平分线, CP是△ABC的一个外角的平分线.若∠ABP=20°, ∠ACP=50°,则∠A+∠P等于( ).
A.70° B.80°
C.90° D.100C解析 ∵BP是△ABC中∠ABC的平分线,CP是△ABC的一个外角的平分线,∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM-∠ABC=60°,
∠ACB=180°-∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°.
∵∠PBC=∠ABP=20°,
∴∠P=180°-∠PBC-∠BCP=30°,
∴∠A+∠P=90°. 故选C.专题六 辅助线的应用【要点指导】在一些几何证明题中, 直接由条件推得结论可能有困难, 这时可以在图形上作一些辅助线, 构造出一些特殊的图形(如平行线、三角形、特殊多边形等), 将题目中的条件进行转化, 从而找到解题思路.例6 如图11-Z-10所示, CD∥AF,∠CDE=∠BAF, AB⊥BC, ∠C=124°, ∠E=80°,试求∠F的度数.解 方法一:延长CB交FA的延长线于点G(如图11-Z-11所示).
∵CD∥AF, ∴∠C+∠G=180°,
∴∠G=180°-∠C=180°-124°=56°,
∴∠BAF=∠G+∠GBA=56°+90°=146°,
∴∠CDE=∠BAF=146°.
∵∠FAB+∠ABC+∠C+∠D+∠E+∠F=(6-2)×180°=720°,
∴∠F=720°-90°-124°-2×146°-80°=134°.方法二:连接AD(如图11-Z-12所示).
∵CD∥AF, ∴∠1=∠2.
在四边形ABCD中, ∵AB⊥BC,
∴∠B=90°,
∴∠BAD+∠1=∠BAD+∠2=∠BAF=360°-(90°+124°)=146°.
∵∠BAF=∠CDE, ∠1=∠2,
∴∠BAD=∠ADE, ∴∠2+∠ADE=∠1+∠BAD=146°,
∴∠F=360°-(146°+80°)=134°.相关题6 [潜江中考] 如图11-Z-13,AB∥EF∥CD, ∠ABC=46°, ∠CEF=154°, 则∠BCE等于( ).
A.16° B.20°
C.23° D.26°B【要点指导】 “分类讨论”体现了化整为零、积零为整的思想.如已知等腰三角形的两边长, 求周长或第三边长, 由于等腰三角形的腰和底不明确, 所以需要分类讨论.专题一 分类讨论思想的运用例1 老师在黑板上出了这样的一道题让同学们讨论:一个等腰三角形的周长为28 cm, 有一边的长为8 cm, 则这个三角形的三边长分别是多少?
李明说应该这样解:若底边长为8 cm, 设腰长为x cm, 则2x+8=28,解得x=10, 所以这个三角形的三边长分别为10 cm, 10 cm, 8 cm;
张纲说不对, 应该这样解:若腰长为8 cm, 设底边长为x cm, 则2×8+x=28, 解得x=12, 所以这个三角形的三边长分别为8 cm, 8 cm, 12 cm.亲爱的同学, 你认为他们的解法对吗?如果不对, 请你写出正确的解答过程.相关题1 有四条线段的长度分别是x-3,x,x+1,x+2(x>3), 则以其中的三条线段为边,一定能组成三角形吗?解 四条线段每三条组成一组,共有四种情况,组合如下:
①x-3,x,x+1;②x-3,x,x+2;③x-3,x+1,x+2;④x,x+1,x+2.
①中x-3+x=2x-3,与x+1相比较:因为x=4时,2x-3=x+1,所以①不一定能组成三角形;
②中x-3+x=2x-3,与x+2相比较:因为x=5时,2x-3=x+2=7,所以②不一定能组成三角形;③中x-3+x+1=2x-2,与x+2相比较:因为x=4时,2x-2=x+2=6, 所以③不一定能组成三角形;
④中x+x+1=2x+1,与x+2相比较:因为x>3,所以2x+1-(x+2)>0,故④一定能组成三角形.【要点指导】方程思想就是通过设未知数建立方程来求解问题的
一种思想. 在解决多边形的问题时, 经常会用到方程思想, 例如:已知多边形的内角和, 求多边形的边数. 如果问题中出现两个未知数, 但相等关系只有一个, 这就需要借助不定方程来求解.专题二 方程思想的运用例2 看图回答问题:(1)内角和为2005°, 小明为什么说不可能?
(2)小亮求的是几边形的内角和?
(3)多加的那个外角的度数你能求出来吗?是多少度呢?又因为n是正整数, 所以n=13,
所以多边形的边数是13, 即小亮求的是十三边形的内角和.
(3)能求出来. 十三边形的内角和是(13-2)×180°=1980°,
所以多加的那个外角的度数是2005°-1980°=25°.相关题2 已知多边形的一个外角与内角和的度数总和为600°, 求此多边形的边数.解 设此多边形的边数为n, 这个外角为x°(0依题意得(n-2)×180+x=600,
即(n-2)×180=600-x.
因为(n-2)×180是180的整数倍, 所以600-x也是180的整数倍,所以x=60, n=5.
即此多边形的边数是5.例3 小马虎同学在计算某个多边形的内角和时得到1840°, 老师说
他算错了, 于是小马虎认真地检查了一遍, 发现漏算了一个内角, 漏算的那个内角是多少度?这个多边形是几边形?解 设漏算的那个内角是x°, 这个多边形是n边形, 则0<x<180,
由题意, 得(n-2)×180-x=1840.
∵n为正整数, ∴1840+x必为180的整数倍.
又∵0<x<180, ∴n=13, x=140.
答:漏算的那个内角是140°, 这个多边形是十三边形.相关题3 [毕节中考]一个多边形纸片按图11-Z-15所示的剪法剪去一个内角后, 得到一个内角和为2340°的新多边形, 则原多边形的边数为( ).
A.13 B.14
C.15 D.16B解析 设原多边形的边数为x,则新多边形的边数为x+1.根据题意列出方程,得(x+1-2)·180=2340,解得x=14.故选B.母题1 (教材P8习题11.1第3题)
对于下面每个三角形, 过顶点A画出中线、角平分线和高.考点:三角形的中线、角平分线和高.
考情:主要考查三角形的高、中线和角平分线的画法及性质.
策略:熟悉三角形的中线、角平分线和高的性质.三角形的中线、角平分线一定在三角形的内部, 而三角形的高的位置与三角形的形状有关.链接1 [连云港中考]小华在电话中问小明:“已知一个三角形的三边长分别是4, 9, 12, 如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( ). C链接2 [贵阳中考]如图11-Z-18, 在△ABC中有四条线段DE, BE, EF, FG, 其中有一条线段是△ABC的中线, 则该线段是( ).
A.线段DE B.线段BE
C.线段EF D.线段FG B分析 根据三角形中线的定义知线段BE是△ABC的中线, 故选B.母题2 (教材P4练习第2题)
(口答)下列长度的三条线段能否组成三角形?为什么?
(1)3, 4, 8;(2)5, 6, 11;(3)5, 6, 10.考点:三角形的三边关系.
考情:主要考查已知两边求第三边的范围或者确定满足条件的三角形的个数.
策略:三角形两边的和大于第三边, 三角形两边的差小于第三边. 在解答有关三角形三边关系的问题时, 应注意分类讨论, 并能根据三边关系进行取舍.链接3 [福建中考]下列各组数中, 能作为一个三角形三边长的是( ).
A.1, 1, 2 B.1, 2, 4
C.2, 3, 4 D.2, 3, 5C链接4 [绥化中考]已知三角形的三边长分别为3, 2a-1, 4, 则a的取值范围是________.分析 ∵三角形的三边长分别为3, 2a-1, 4,
∴4-3<2a-1<4+3,
即1<a<4.1<a<4母题3 (教材P17习题11.2第11题)
如图11-Z-19, CE是△ABC的外角∠ACD的平分线, 且CE交BA的延长线于点E. 求证:∠BAC=∠B+2∠E.考点:三角形的内角和公式及外角的性质.
考情:三角形的角度计算常常运用内角和公式与外角的性质, 且常与平行线、角平分线、高结合在一起考查.
策略:(1)三角形三个内角的和等于180°;(2)三角形的外角等于与它不相邻的两个内角的和.链接5 [ 乐山中考]如图11-Z-20, CE是△ABC的外角∠ACD的平分线. 若∠B=35°,∠ACE=60°, 则∠A等于( ).
A.35° B.95°
C.85° D.75° C链接6 [襄阳中考]如图11-Z-21, AD是∠EAC的平分线, AD∥BC, ∠B=30°,则∠C的度数为( ).
A.50° B.40°
C.30° D.20°C母题4 (教材P14练习第2题)
如图11-Z-22, ∠C=90°, ∠1=∠2, △ADE是直角三角形吗?为什么?考点:直角三角形的性质与判定.
考情:直角三角形的两个锐角互余的性质常与其他知识综合考查.
策略:(1)直角三角形的两个锐角互余;(2)有两个角互余的三角形是直角三角形.链接7 [襄阳中考]如图11-Z-23, BC⊥AE于点C, CD∥AB, ∠B=55°, 则∠1的度数为( ).
A.35° B.45°
C.55° D.65°A母题5 (教材P25习题11.3第5题)
一个多边形的内角和等于1260°, 它是几边形?考点:多边形的内角和公式.
考情:已知多边形的内角和, 求多边形的边数.
策略:(1)结合多边形的内角和公式, 寻求等量关系, 构建方程求解;
(2)利用多边形的外角和等于360°以及邻补角的性质求解.链接8 [自贡中考]若一个多边形的内角和比它的外角和的3倍少180°, 则它的边数是_____ .7分析 设这个多边形的边数为n, 则3×360°-(n-2)×180°=180°, 解得n=7.链接9 [巴中中考]若一个正多边形的一个内角等于135°, 则这个多边形是正____边形.八分析 设该多边形的边数为n. 根据题意, 得(n-2)×180°=n×135°, 解得n=8.解 (1)设矩形的长为x厘米, 则宽为(28-x)厘 米. 依题意有 x(28-x)=180, 解得x1=10, x2=18, 当x=10时, 28-x=18>10, 不合题意, 舍去;当 x=18时, 28-x=10, 符合题意. 故它的长为18厘米, 宽为10厘米.
(2)假设能围成, 设围成的矩形的长为y厘米, 则宽为(28-y)厘米.
依题意有y(28-y)=200, 即y2-28y+200=0.
∵Δ=b2-4ac=(-28)2-4×1×200=-16<0, ∴原方程无实数根.
故不能将周长为56厘米的矩形改成面积为 200平方厘米的矩形.
谢 谢 观 看!
有关的角与三角形
有关的角三角形三个内角的和等于180°三角形
的外角三角形的外角
和等于360°三角形的外角等于与它不相邻的两个内角的和直角三角形性质直角三角形的两个锐角互余判定有两个角互余的三角形是直角三角形与三角形有关的线段高中
线角平分线三条高(或三条高所在的直线)相交于一点分对边相等, 分得的两
个三角形的面积相等三条中线相交于三角形内部一点, 该点为三角形的重心三角形内角被分
成的两个角相等三条角平分线相交于三角形内部一点多边形及其内角和多边形的内角和n边形内角和:(n-2)×180°多边形的外角和:360°n边形对角线的条数:正n
边形不稳定性(三角形除外)每条边都相等每个角都相等, 为180°-每个外角都相等, 为【要点指导】确定一个图形中三角形的个数时, 应用分类讨论思想和枚举法按照一定的规律来计数, 如按照不同的边或顶点来寻找.专题一 三角形的计数例1 图11-Z-1中, 若∠BAC为锐角, 则一共有____个三角形, 其中锐角三角形有____个, 直角三角形有____个, 钝角三角形有____个. 623 1分析 相关题1 如图11-Z-2, 在△ABC中,AD, BF, CE相交于点O, 则图中的三角形有( ).
A.7个 B.10个
C.15个 D.16个D【要点指导】“直角三角形的两锐角互余”是直角三角形的性质;“有两个角互余的三角形是直角三角形”是直角三角形的判定. 在运用直角三角形的性质和判定的过程中, 常与三角形的角平分线、高等结合在一起.专题二 直角三角形的有关计算例2 如图11-Z-3所示, ∠BAC=90°,∠1=∠2, AM⊥BC, AD⊥BE, 垂足分别为M, F,那么∠2=∠3=∠4, 你知道这是为什么吗?解 在Rt△BDF与Rt△ADM中,
∵∠2+∠ADB=90°, ∠3+∠ADB=90°,
∴∠2=∠3.
在Rt△ABE与Rt△AEF中,
∵∠1+∠AEB=90°, ∠4+∠AEB=90°,
∴∠1=∠4.
又∵∠1=∠2, ∴∠2=∠3=∠4.相关题2-1 如图11-Z-4, Rt△ABC的两个锐角的平分线AE,BD所夹的锐角∠AOD是( ).
A.30° B.60°
C.45° D.15°或75°C相关题2-2 如图11-Z-5所示, 已知在△ABC中, ∠ACB=90°,CD为AB边上的高, ∠ABC的平分线BE与CD, CA分别交于点F, E, 则下列结论正确的是( ).
①∠CFE=∠CEF; ②∠FCB=∠FBC;
③∠A=∠DCB;
④∠CFE与∠CBF互余.
A.①③④ B.②③④
C.①②④ D.①②③A【要点指导】三角形任意两边之和大于第三边, 任意两边之差小于
第三边, 这两种关系可用一句话来概括:设三角形的三边长分别为a, b, c,则|b-c|
解得b=2,c=3.
由方程|x-4|=2,得x-4=2或x-4=-2,
∴x=6或x=2,即a=6或a=2.当a=6时,2+3<6,不能组成三角形,故舍去;
当a=2时,2+2>3,能组成三角形,
∴a=2,b=2,c=3.
∵2+2+3=7,
∴△ABC的周长为7.专题四 复杂图形中角度的计算【要点指导】求复杂图形中的角度时, 常利用转化的思想将分散的角转化到一个多边形中, 再利用多边形的内角和与外角和来解答.例4 [泰安中考]如图11-Z-6, 求∠A+∠B+∠BCD+∠D+∠E+ ∠EFG+∠G的度数.相关题4 如图11-Z-7所示, ∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )度.
A.450 B.540
C.630 D.720B专题五 三角形内角和定理与外角的性质【要点指导】三角形内角和定理与外角的性质是求解与角有关问题的主要依据, 是中考的热点内容, 在中考题中主要以填空题、选择题的形式出现, 解答题中也常用到一些有关的知识.例5 [泰安中考]如图11-Z-8, 在△ABC中, D是BC边上一点,
∠1=∠2, ∠3=∠4, ∠BAC=63°, 求∠DAC的度数.解 设∠1=∠2=x, 则∠3=∠4=2x.
∵∠BAC=63°, ∴∠2+∠4=117°,
即x+2x=117°, 解得x=39°,
∴∠3=∠4=78°,
∴∠DAC=180°-∠3-∠4=24°.相关题5 如图11-Z-9, BP是△ABC中∠ABC的平分线, CP是△ABC的一个外角的平分线.若∠ABP=20°, ∠ACP=50°,则∠A+∠P等于( ).
A.70° B.80°
C.90° D.100C解析 ∵BP是△ABC中∠ABC的平分线,CP是△ABC的一个外角的平分线,∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM-∠ABC=60°,
∠ACB=180°-∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°.
∵∠PBC=∠ABP=20°,
∴∠P=180°-∠PBC-∠BCP=30°,
∴∠A+∠P=90°. 故选C.专题六 辅助线的应用【要点指导】在一些几何证明题中, 直接由条件推得结论可能有困难, 这时可以在图形上作一些辅助线, 构造出一些特殊的图形(如平行线、三角形、特殊多边形等), 将题目中的条件进行转化, 从而找到解题思路.例6 如图11-Z-10所示, CD∥AF,∠CDE=∠BAF, AB⊥BC, ∠C=124°, ∠E=80°,试求∠F的度数.解 方法一:延长CB交FA的延长线于点G(如图11-Z-11所示).
∵CD∥AF, ∴∠C+∠G=180°,
∴∠G=180°-∠C=180°-124°=56°,
∴∠BAF=∠G+∠GBA=56°+90°=146°,
∴∠CDE=∠BAF=146°.
∵∠FAB+∠ABC+∠C+∠D+∠E+∠F=(6-2)×180°=720°,
∴∠F=720°-90°-124°-2×146°-80°=134°.方法二:连接AD(如图11-Z-12所示).
∵CD∥AF, ∴∠1=∠2.
在四边形ABCD中, ∵AB⊥BC,
∴∠B=90°,
∴∠BAD+∠1=∠BAD+∠2=∠BAF=360°-(90°+124°)=146°.
∵∠BAF=∠CDE, ∠1=∠2,
∴∠BAD=∠ADE, ∴∠2+∠ADE=∠1+∠BAD=146°,
∴∠F=360°-(146°+80°)=134°.相关题6 [潜江中考] 如图11-Z-13,AB∥EF∥CD, ∠ABC=46°, ∠CEF=154°, 则∠BCE等于( ).
A.16° B.20°
C.23° D.26°B【要点指导】 “分类讨论”体现了化整为零、积零为整的思想.如已知等腰三角形的两边长, 求周长或第三边长, 由于等腰三角形的腰和底不明确, 所以需要分类讨论.专题一 分类讨论思想的运用例1 老师在黑板上出了这样的一道题让同学们讨论:一个等腰三角形的周长为28 cm, 有一边的长为8 cm, 则这个三角形的三边长分别是多少?
李明说应该这样解:若底边长为8 cm, 设腰长为x cm, 则2x+8=28,解得x=10, 所以这个三角形的三边长分别为10 cm, 10 cm, 8 cm;
张纲说不对, 应该这样解:若腰长为8 cm, 设底边长为x cm, 则2×8+x=28, 解得x=12, 所以这个三角形的三边长分别为8 cm, 8 cm, 12 cm.亲爱的同学, 你认为他们的解法对吗?如果不对, 请你写出正确的解答过程.相关题1 有四条线段的长度分别是x-3,x,x+1,x+2(x>3), 则以其中的三条线段为边,一定能组成三角形吗?解 四条线段每三条组成一组,共有四种情况,组合如下:
①x-3,x,x+1;②x-3,x,x+2;③x-3,x+1,x+2;④x,x+1,x+2.
①中x-3+x=2x-3,与x+1相比较:因为x=4时,2x-3=x+1,所以①不一定能组成三角形;
②中x-3+x=2x-3,与x+2相比较:因为x=5时,2x-3=x+2=7,所以②不一定能组成三角形;③中x-3+x+1=2x-2,与x+2相比较:因为x=4时,2x-2=x+2=6, 所以③不一定能组成三角形;
④中x+x+1=2x+1,与x+2相比较:因为x>3,所以2x+1-(x+2)>0,故④一定能组成三角形.【要点指导】方程思想就是通过设未知数建立方程来求解问题的
一种思想. 在解决多边形的问题时, 经常会用到方程思想, 例如:已知多边形的内角和, 求多边形的边数. 如果问题中出现两个未知数, 但相等关系只有一个, 这就需要借助不定方程来求解.专题二 方程思想的运用例2 看图回答问题:(1)内角和为2005°, 小明为什么说不可能?
(2)小亮求的是几边形的内角和?
(3)多加的那个外角的度数你能求出来吗?是多少度呢?又因为n是正整数, 所以n=13,
所以多边形的边数是13, 即小亮求的是十三边形的内角和.
(3)能求出来. 十三边形的内角和是(13-2)×180°=1980°,
所以多加的那个外角的度数是2005°-1980°=25°.相关题2 已知多边形的一个外角与内角和的度数总和为600°, 求此多边形的边数.解 设此多边形的边数为n, 这个外角为x°(0
即(n-2)×180=600-x.
因为(n-2)×180是180的整数倍, 所以600-x也是180的整数倍,所以x=60, n=5.
即此多边形的边数是5.例3 小马虎同学在计算某个多边形的内角和时得到1840°, 老师说
他算错了, 于是小马虎认真地检查了一遍, 发现漏算了一个内角, 漏算的那个内角是多少度?这个多边形是几边形?解 设漏算的那个内角是x°, 这个多边形是n边形, 则0<x<180,
由题意, 得(n-2)×180-x=1840.
∵n为正整数, ∴1840+x必为180的整数倍.
又∵0<x<180, ∴n=13, x=140.
答:漏算的那个内角是140°, 这个多边形是十三边形.相关题3 [毕节中考]一个多边形纸片按图11-Z-15所示的剪法剪去一个内角后, 得到一个内角和为2340°的新多边形, 则原多边形的边数为( ).
A.13 B.14
C.15 D.16B解析 设原多边形的边数为x,则新多边形的边数为x+1.根据题意列出方程,得(x+1-2)·180=2340,解得x=14.故选B.母题1 (教材P8习题11.1第3题)
对于下面每个三角形, 过顶点A画出中线、角平分线和高.考点:三角形的中线、角平分线和高.
考情:主要考查三角形的高、中线和角平分线的画法及性质.
策略:熟悉三角形的中线、角平分线和高的性质.三角形的中线、角平分线一定在三角形的内部, 而三角形的高的位置与三角形的形状有关.链接1 [连云港中考]小华在电话中问小明:“已知一个三角形的三边长分别是4, 9, 12, 如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( ). C链接2 [贵阳中考]如图11-Z-18, 在△ABC中有四条线段DE, BE, EF, FG, 其中有一条线段是△ABC的中线, 则该线段是( ).
A.线段DE B.线段BE
C.线段EF D.线段FG B分析 根据三角形中线的定义知线段BE是△ABC的中线, 故选B.母题2 (教材P4练习第2题)
(口答)下列长度的三条线段能否组成三角形?为什么?
(1)3, 4, 8;(2)5, 6, 11;(3)5, 6, 10.考点:三角形的三边关系.
考情:主要考查已知两边求第三边的范围或者确定满足条件的三角形的个数.
策略:三角形两边的和大于第三边, 三角形两边的差小于第三边. 在解答有关三角形三边关系的问题时, 应注意分类讨论, 并能根据三边关系进行取舍.链接3 [福建中考]下列各组数中, 能作为一个三角形三边长的是( ).
A.1, 1, 2 B.1, 2, 4
C.2, 3, 4 D.2, 3, 5C链接4 [绥化中考]已知三角形的三边长分别为3, 2a-1, 4, 则a的取值范围是________.分析 ∵三角形的三边长分别为3, 2a-1, 4,
∴4-3<2a-1<4+3,
即1<a<4.1<a<4母题3 (教材P17习题11.2第11题)
如图11-Z-19, CE是△ABC的外角∠ACD的平分线, 且CE交BA的延长线于点E. 求证:∠BAC=∠B+2∠E.考点:三角形的内角和公式及外角的性质.
考情:三角形的角度计算常常运用内角和公式与外角的性质, 且常与平行线、角平分线、高结合在一起考查.
策略:(1)三角形三个内角的和等于180°;(2)三角形的外角等于与它不相邻的两个内角的和.链接5 [ 乐山中考]如图11-Z-20, CE是△ABC的外角∠ACD的平分线. 若∠B=35°,∠ACE=60°, 则∠A等于( ).
A.35° B.95°
C.85° D.75° C链接6 [襄阳中考]如图11-Z-21, AD是∠EAC的平分线, AD∥BC, ∠B=30°,则∠C的度数为( ).
A.50° B.40°
C.30° D.20°C母题4 (教材P14练习第2题)
如图11-Z-22, ∠C=90°, ∠1=∠2, △ADE是直角三角形吗?为什么?考点:直角三角形的性质与判定.
考情:直角三角形的两个锐角互余的性质常与其他知识综合考查.
策略:(1)直角三角形的两个锐角互余;(2)有两个角互余的三角形是直角三角形.链接7 [襄阳中考]如图11-Z-23, BC⊥AE于点C, CD∥AB, ∠B=55°, 则∠1的度数为( ).
A.35° B.45°
C.55° D.65°A母题5 (教材P25习题11.3第5题)
一个多边形的内角和等于1260°, 它是几边形?考点:多边形的内角和公式.
考情:已知多边形的内角和, 求多边形的边数.
策略:(1)结合多边形的内角和公式, 寻求等量关系, 构建方程求解;
(2)利用多边形的外角和等于360°以及邻补角的性质求解.链接8 [自贡中考]若一个多边形的内角和比它的外角和的3倍少180°, 则它的边数是_____ .7分析 设这个多边形的边数为n, 则3×360°-(n-2)×180°=180°, 解得n=7.链接9 [巴中中考]若一个正多边形的一个内角等于135°, 则这个多边形是正____边形.八分析 设该多边形的边数为n. 根据题意, 得(n-2)×180°=n×135°, 解得n=8.解 (1)设矩形的长为x厘米, 则宽为(28-x)厘 米. 依题意有 x(28-x)=180, 解得x1=10, x2=18, 当x=10时, 28-x=18>10, 不合题意, 舍去;当 x=18时, 28-x=10, 符合题意. 故它的长为18厘米, 宽为10厘米.
(2)假设能围成, 设围成的矩形的长为y厘米, 则宽为(28-y)厘米.
依题意有y(28-y)=200, 即y2-28y+200=0.
∵Δ=b2-4ac=(-28)2-4×1×200=-16<0, ∴原方程无实数根.
故不能将周长为56厘米的矩形改成面积为 200平方厘米的矩形.
谢 谢 观 看!
