苏科版八年级数学上册第二章轴对称图形2.5 等腰三角形的轴对称性课件(共20张)
文档属性
| 名称 | 苏科版八年级数学上册第二章轴对称图形2.5 等腰三角形的轴对称性课件(共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 19:17:23 | ||
图片预览



文档简介
课件20张PPT。 等腰三角形的轴对称性初中数学八年级上册
(苏科版)
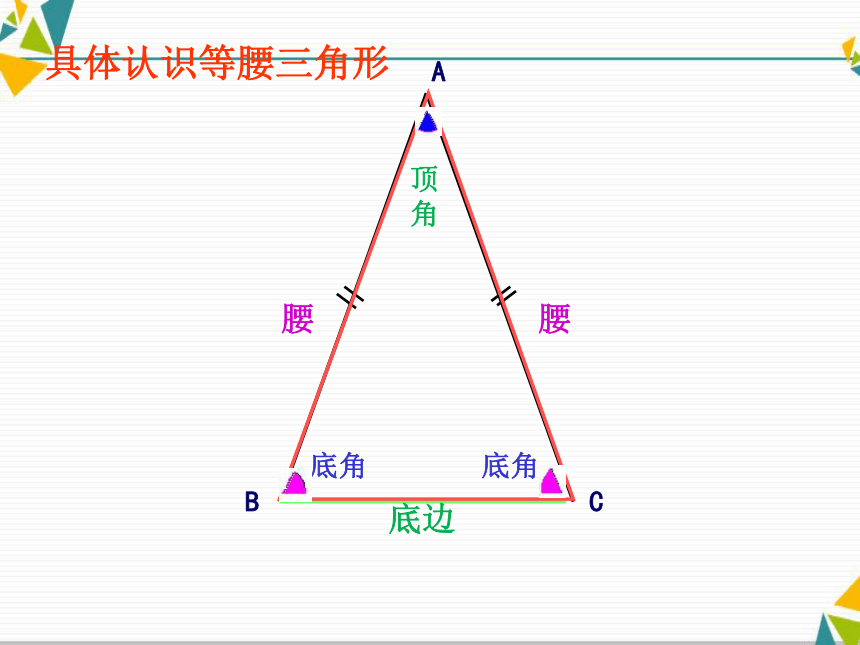
埃及金字塔(一)创设情境,激发兴趣具体认识等腰三角形ACB腰 腰底角底角顶角底边
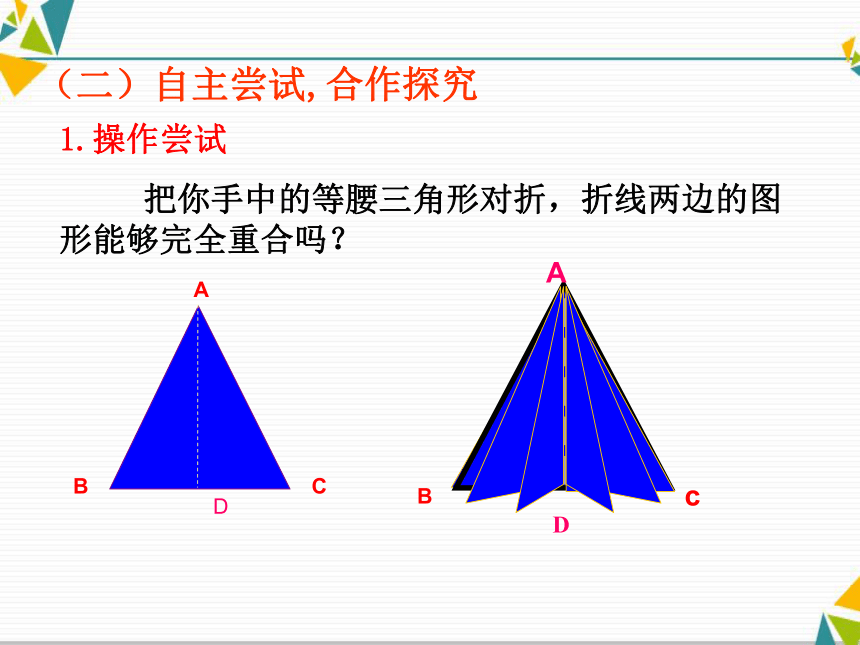
1.操作尝试
把你手中的等腰三角形对折,折线两边的图形能够完全重合吗?(二)自主尝试,合作探究
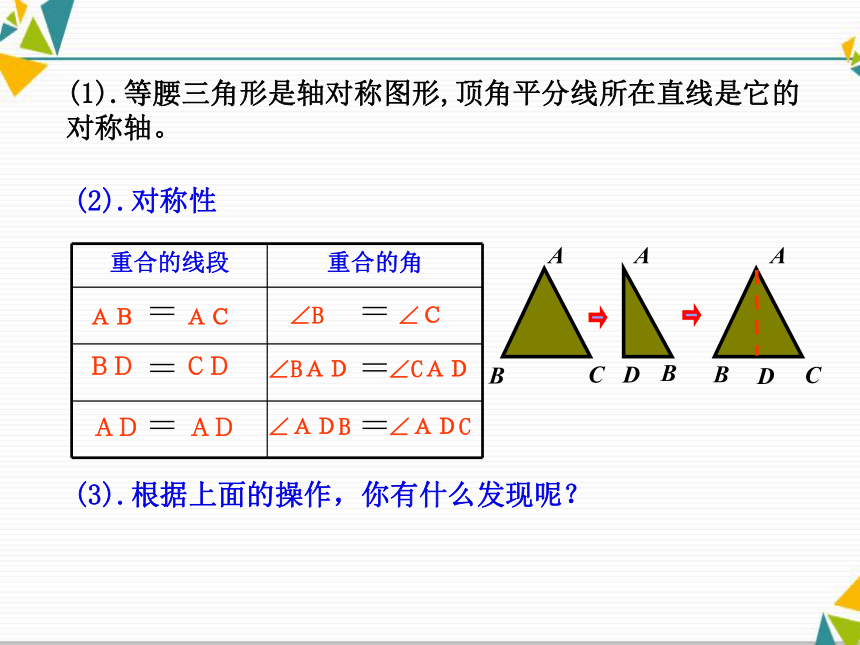
(1).等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。
(2).对称性 AB AC BD CD AD AD∠B ∠C ∠BAD ∠CAD ∠ADB ∠ADC (3).根据上面的操作,你有什么发现呢?性质1:在△ABC中,
∵ AB=AC( 已知)
∴ ∠B=∠C (等边对等角)
等腰三角形性质用几何语言表示为:
ABC 等腰三角形的两底角相等。
(简称“等边对等角”)
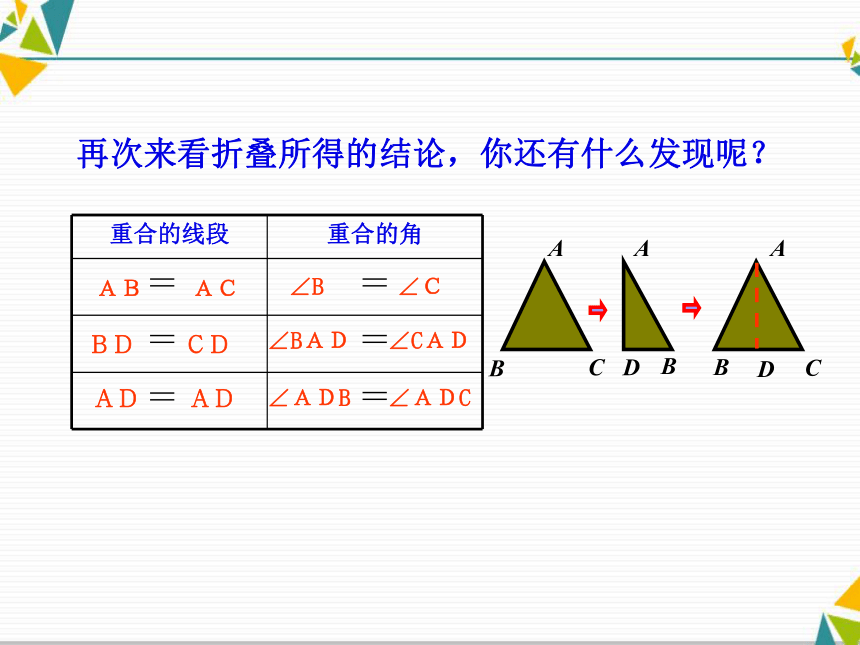
再次来看折叠所得的结论,你还有什么发现呢?
AB AC BD CD AD AD∠B ∠C ∠BAD ∠CAD ∠ADB ∠ADC 请利用“三线合一”的性质,完成下列填空题。
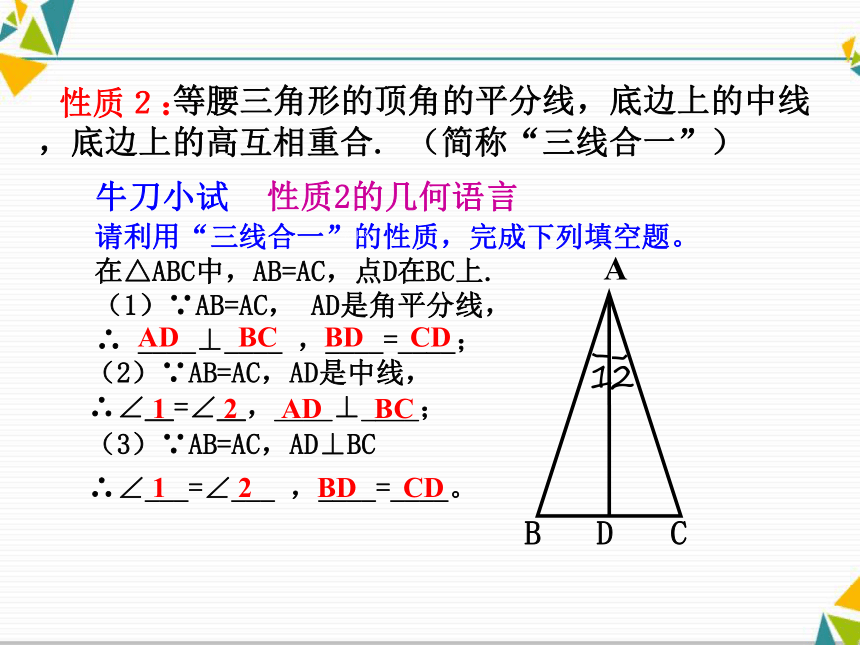
在△ABC中,AB=AC,点D在BC上.
(1)∵AB=AC, AD是角平分线,
∴ ____⊥____ ,____=____;
牛刀小试学科网 等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合. (简称“三线合一”)
性质2的几何语言性质2:
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;(3)∵AB=AC,AD⊥BC
∴∠___=∠___ ,____=____。
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。 等腰三角形的两底角相等。
(简称“等边对等角”) 等腰三角形的顶角的平分线,底边
上的中线,底边上的高互相重合.
(简称“三线合一”)2.等腰三角形性质1.等腰三角形的轴对称性性质1:性质2:(1).如图,在△ABC中,AB=AC ①如果∠B=80°,那么∠C= ____. ∠A= ____.
②如果∠A=80°,那么∠B= ____. ∠C= ____.80°20°50°50°(2).如果等腰三角形一个底角为80°,它的另外
两个角为________ . 80°, 20°(3).如果等腰三角形一个角为80°,它的另外两
个角为 _____________________ . 80°, 20°或 50°, 50°比一比,看谁做得快14或16 (4).已知等腰三角形的两边长分别是4和6,则
它的周长是________. (5).已知等腰三角形的两边长分别是3和7,则
它的周长是________ .17 方法总结
对于等腰三角形的角,若没有明确说是顶角还
是底角,则需要分类讨论。
同样对于等腰三角形的边,若没有明确说是腰
还是底边,也需要分类讨论。2.操作尝试 按下列作法,用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.作 法图 形1.作线段BC= a2.作线段BC的垂直平分线MN,MN交BC于点D.3.在MN上截取线段DA,使DA= h.4.连接AB、AC.
△ABC就是所求作的等腰三角形(三)谨思笃行,连绵思活例1.如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
证明:
∵AB=AC, AD = BD
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C =∠1
∵∠ADB是△ADC的外角,
∴ ∠ADB =∠C +∠2.
∴ ∠ADB =∠1 +∠2 =∠BAC.
12例2.如图,在等腰三角形ABC中,AB=AC,M、N在BC上,且AM=AN,BM与CN相等吗?请说明理由.
D∟证明:作△ABC 的高线AD
在△ABC中
∵ AB=AC,AD⊥BC
∴BD=CD (三线合一)
同理,MD=ND
∴ BD - MD = CD - ND
即BM=CN
方法总结:
等腰三角形顶角平分线及底边上的中线、高线是常用
的辅助线,通过添画辅助线,把一个等腰三角形分成一对
全等三角形。︶︶︶︶1234︶︵(四)拓展训练,能力提升 如图,在△ABC 中,AB=AC, AF⊥BC,点D 在BA的延
长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,
并证明你的结论。
3 124︶︵︶︶解: DE∥AF
在△ABC中
∵ AB=AC ,AF⊥BC
∴ ∠BAF = ∠ CAF (三线合一)
∵ AD=AE
∴ ∠ADE = ∠AED
∵∠BAC是△ADE的外角,
∴ ∠ BAC = ∠ADE +∠AED =2∠AED .
∵ ∠ BAC = ∠BAF + ∠ CAF = 2∠CAF
∴ ∠AED = ∠CAF
∴ DE∥AF通过本节课的学习,你的收获是……(五)课堂小结,感悟收获
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。 等腰三角形的两底角相等。
(简称“等边对等角”) 等腰三角形的顶角的平分线,底边
上的中线,底边上的高互相重合.
(简称“三线合一”)2.等腰三角形性质1.等腰三角形的轴对称性性质1:性质2:(六)作业布置必做题:
1.等腰三角形的周长是10,一边长是4,则其它两边长为
____________。
2.(1)如果等腰三角形有一个角等于120°,则其余两个角分别是___________。
(2)如果等腰三角形有一个角等于55°,则其余两个角分别是___________。
选做题:已知:如图,∠A=∠D=90°,AB=CD,AC与BD相
交于点F,E是BC的中点. 求证:∠BFE=∠CFE.
谢谢勤奋是你生命的密码,
能译出你一部壮丽的史诗。
(苏科版)
埃及金字塔(一)创设情境,激发兴趣具体认识等腰三角形ACB腰 腰底角底角顶角底边
1.操作尝试
把你手中的等腰三角形对折,折线两边的图形能够完全重合吗?(二)自主尝试,合作探究
(1).等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。
(2).对称性 AB AC BD CD AD AD∠B ∠C ∠BAD ∠CAD ∠ADB ∠ADC (3).根据上面的操作,你有什么发现呢?性质1:在△ABC中,
∵ AB=AC( 已知)
∴ ∠B=∠C (等边对等角)
等腰三角形性质用几何语言表示为:
ABC 等腰三角形的两底角相等。
(简称“等边对等角”)
再次来看折叠所得的结论,你还有什么发现呢?
AB AC BD CD AD AD∠B ∠C ∠BAD ∠CAD ∠ADB ∠ADC 请利用“三线合一”的性质,完成下列填空题。
在△ABC中,AB=AC,点D在BC上.
(1)∵AB=AC, AD是角平分线,
∴ ____⊥____ ,____=____;
牛刀小试学科网 等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合. (简称“三线合一”)
性质2的几何语言性质2:
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;(3)∵AB=AC,AD⊥BC
∴∠___=∠___ ,____=____。
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。 等腰三角形的两底角相等。
(简称“等边对等角”) 等腰三角形的顶角的平分线,底边
上的中线,底边上的高互相重合.
(简称“三线合一”)2.等腰三角形性质1.等腰三角形的轴对称性性质1:性质2:(1).如图,在△ABC中,AB=AC ①如果∠B=80°,那么∠C= ____. ∠A= ____.
②如果∠A=80°,那么∠B= ____. ∠C= ____.80°20°50°50°(2).如果等腰三角形一个底角为80°,它的另外
两个角为________ . 80°, 20°(3).如果等腰三角形一个角为80°,它的另外两
个角为 _____________________ . 80°, 20°或 50°, 50°比一比,看谁做得快14或16 (4).已知等腰三角形的两边长分别是4和6,则
它的周长是________. (5).已知等腰三角形的两边长分别是3和7,则
它的周长是________ .17 方法总结
对于等腰三角形的角,若没有明确说是顶角还
是底角,则需要分类讨论。
同样对于等腰三角形的边,若没有明确说是腰
还是底边,也需要分类讨论。2.操作尝试 按下列作法,用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.作 法图 形1.作线段BC= a2.作线段BC的垂直平分线MN,MN交BC于点D.3.在MN上截取线段DA,使DA= h.4.连接AB、AC.
△ABC就是所求作的等腰三角形(三)谨思笃行,连绵思活例1.如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
证明:
∵AB=AC, AD = BD
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C =∠1
∵∠ADB是△ADC的外角,
∴ ∠ADB =∠C +∠2.
∴ ∠ADB =∠1 +∠2 =∠BAC.
12例2.如图,在等腰三角形ABC中,AB=AC,M、N在BC上,且AM=AN,BM与CN相等吗?请说明理由.
D∟证明:作△ABC 的高线AD
在△ABC中
∵ AB=AC,AD⊥BC
∴BD=CD (三线合一)
同理,MD=ND
∴ BD - MD = CD - ND
即BM=CN
方法总结:
等腰三角形顶角平分线及底边上的中线、高线是常用
的辅助线,通过添画辅助线,把一个等腰三角形分成一对
全等三角形。︶︶︶︶1234︶︵(四)拓展训练,能力提升 如图,在△ABC 中,AB=AC, AF⊥BC,点D 在BA的延
长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,
并证明你的结论。
3 124︶︵︶︶解: DE∥AF
在△ABC中
∵ AB=AC ,AF⊥BC
∴ ∠BAF = ∠ CAF (三线合一)
∵ AD=AE
∴ ∠ADE = ∠AED
∵∠BAC是△ADE的外角,
∴ ∠ BAC = ∠ADE +∠AED =2∠AED .
∵ ∠ BAC = ∠BAF + ∠ CAF = 2∠CAF
∴ ∠AED = ∠CAF
∴ DE∥AF通过本节课的学习,你的收获是……(五)课堂小结,感悟收获
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。 等腰三角形的两底角相等。
(简称“等边对等角”) 等腰三角形的顶角的平分线,底边
上的中线,底边上的高互相重合.
(简称“三线合一”)2.等腰三角形性质1.等腰三角形的轴对称性性质1:性质2:(六)作业布置必做题:
1.等腰三角形的周长是10,一边长是4,则其它两边长为
____________。
2.(1)如果等腰三角形有一个角等于120°,则其余两个角分别是___________。
(2)如果等腰三角形有一个角等于55°,则其余两个角分别是___________。
选做题:已知:如图,∠A=∠D=90°,AB=CD,AC与BD相
交于点F,E是BC的中点. 求证:∠BFE=∠CFE.
谢谢勤奋是你生命的密码,
能译出你一部壮丽的史诗。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
