2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷(PDF版含答案)
文档属性
| 名称 | 2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷(PDF版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-01 00:00:00 | ||
图片预览



文档简介
第 1页(共 15页)
2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷
一、选择题(共 10小题,每小题 4分,共 40分)
1.(4分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(4分)如图所示,在△ABC中,∠C=90°,则∠B为( )
A.15° B.30° C.50° D.60°
3.(4分)将点 A(4,2)向左平移 2个单位长度得到点 A′,则点 A′的坐标是( )
A.(6,2) B.(4,0) C.(2,2) D.(4,4)
4.(4分)下列各式中,不是二次根式的是( )
A. B. C.﹣ D.
5.(4分)在 Rt△ABC中,a=3,b=5,则 c的长为( )
A.2 B. C.4 D.4或
6.(4分)下列说法错误的是( )
A.一组对边平行且相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的菱形是正方形
D.对角线相等的平行四边形是矩形
7.(4分)下面哪个点在函数 y= x+1的图象上( )
A.(2,1) B.(﹣2,1) C.(2,0) D.(﹣2,0)
8.(4分)若等腰三角形的周长为 60cm,底边长为 x cm,一腰长为 y cm,则 y与 x的函数关系式及自变量 x的取值
范围是( )
A.y=60﹣2x(0<x<60) B.y=60﹣2x(0<x<30)
C.y= (60﹣x)(0<x<60) D.y= (60﹣x)(0<x<30)
第 2页(共 15页)
9.(4分)将 100个数据分成①~⑧组,如下表所示:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 4 8 12 24 18 7 3
那么第④组的频率为( )
A.24 B.26 C.0.24 D.0.26
10.(4分)无论 m取任何实数,直线 y=x+m与 y=﹣x+4的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二.填空题(共 8小题,每小题 4分,共 32分)
11.(4分)函数 y= 中自变量 x的取值范围是 .
12.(4分)正多边形的一个内角等于 144°,则该多边形是正 边形.
13.(4分)已知菱形 ABCD中,对角线 AC=6,BD=8,则菱形 ABCD的周长是 ,面积是 .
14.(4分)把容量是 64的样本分成 8组,从第 1组到第 4组的频数分别是 5,7,11,13,第 5组到第 7组的频率
是 0.125,那么第 8组的频数是 .
15.(4分)如图,在矩形 ABCD中,对角线 AC、BD相交于点 O,点 E、F分别是 AO、AD的中点,若 AB=6cm,
BC=8cm,则△AEF的周长= cm.
16.(4分)一次函数 y=﹣2x+m的图象经过点 P(﹣2,3),且与 x轴、y轴分别交于点 A、B,则△AOB的面积等
于 .
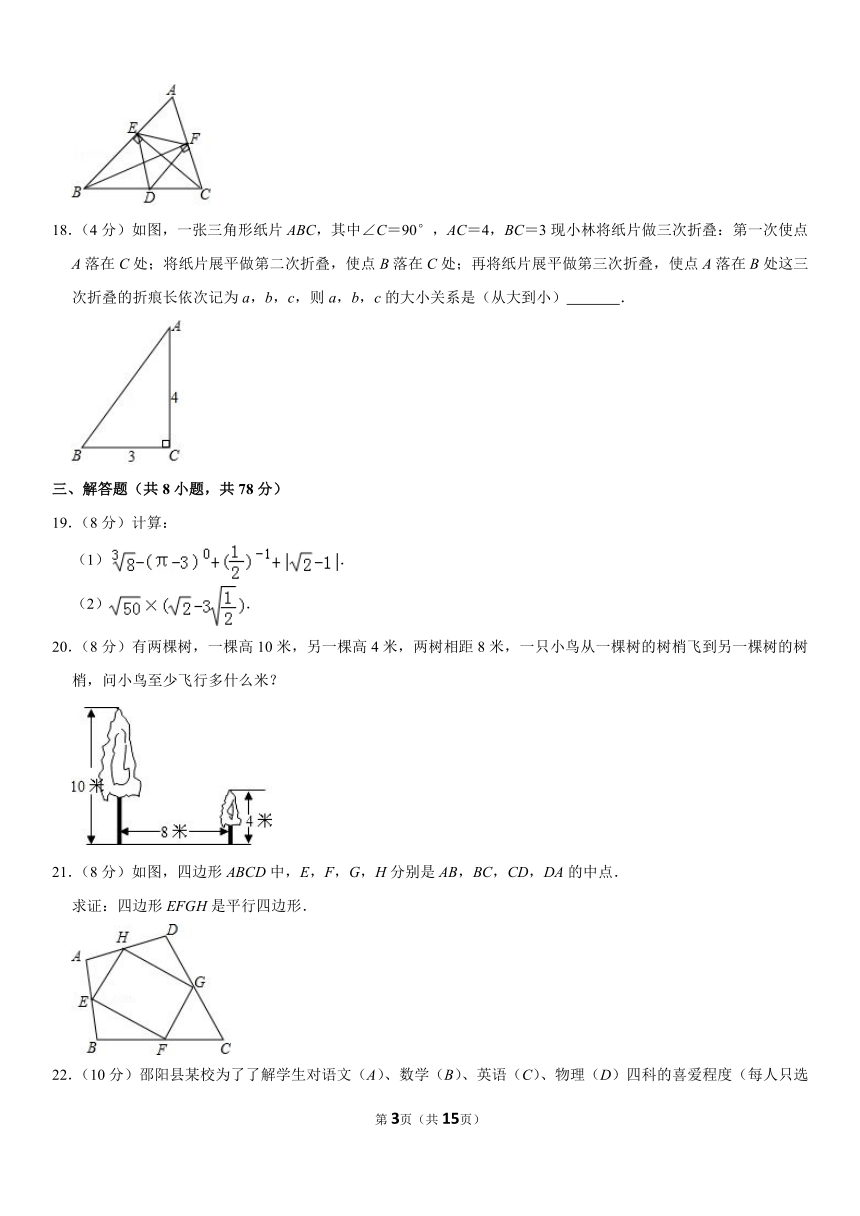
17.(4分)如图,D是△ABC中 BC边中点,∠EDF=60°,CE⊥AB于 E,BF⊥AC于 F,若 EF=4,则 BC= .
第 3页(共 15页)
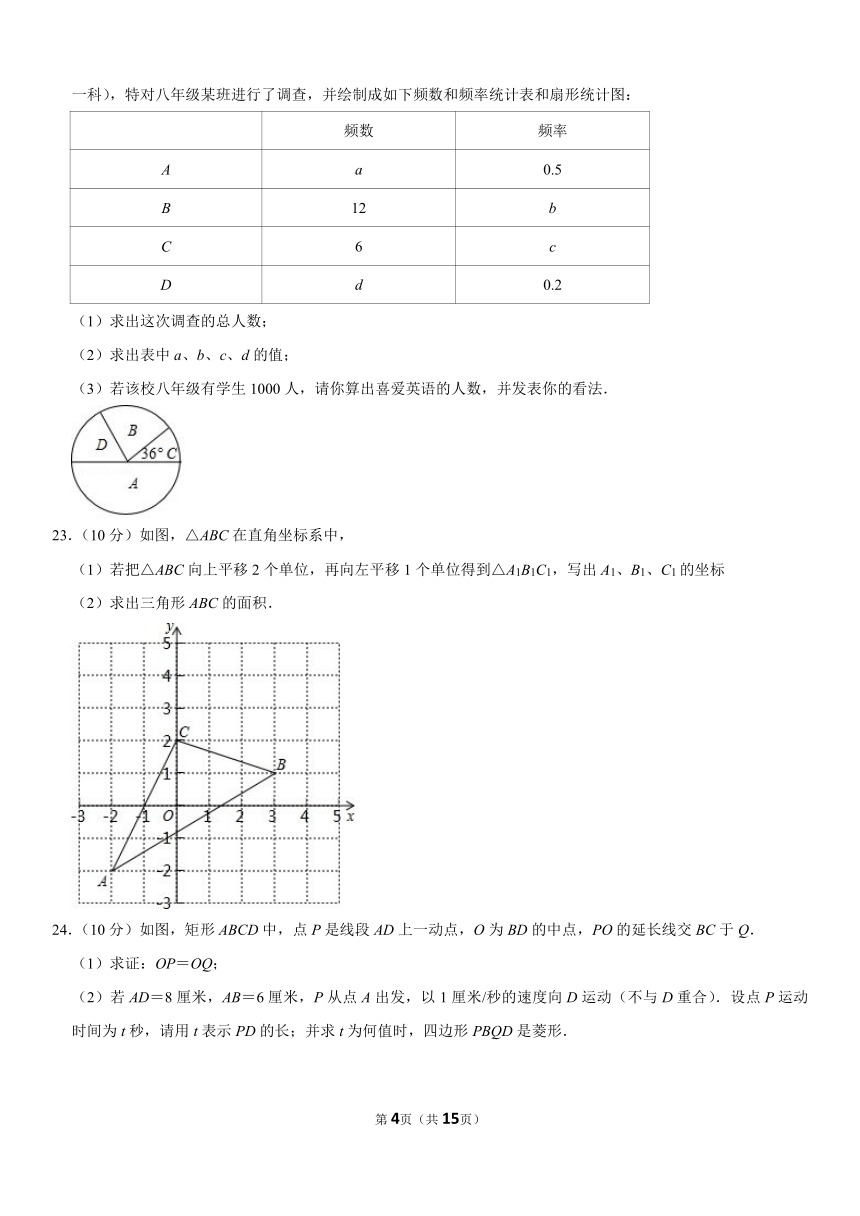
18.(4分)如图,一张三角形纸片 ABC,其中∠C=90°,AC=4,BC=3现小林将纸片做三次折叠:第一次使点
A落在 C处;将纸片展平做第二次折叠,使点 B落在 C处;再将纸片展平做第三次折叠,使点 A落在 B处这三
次折叠的折痕长依次记为 a,b,c,则 a,b,c的大小关系是(从大到小) .
三、解答题(共 8小题,共 78分)
19.(8分)计算:
(1) .
(2) .
20.(8分)有两棵树,一棵高 10米,另一棵高 4米,两树相距 8米,一只小鸟从一棵树的树梢飞到另一棵树的树
梢,问小鸟至少飞行多什么米?
21.(8分)如图,四边形 ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点.
求证:四边形 EFGH是平行四边形.
22.(10分)邵阳县某校为了了解学生对语文(A)、数学(B)、英语(C)、物理(D)四科的喜爱程度(每人只选
第 4页(共 15页)
一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
频数 频率
A a 0.5
B 12 b
C 6 c
D d 0.2
(1)求出这次调查的总人数;
(2)求出表中 a、b、c、d的值;
(3)若该校八年级有学生 1000人,请你算出喜爱英语的人数,并发表你的看法.
23.(10分)如图,△ABC在直角坐标系中,
(1)若把△ABC向上平移 2个单位,再向左平移 1个单位得到△A1B1C1,写出 A1、B1、C1的坐标
(2)求出三角形 ABC的面积.
24.(10分)如图,矩形 ABCD中,点 P是线段 AD上一动点,O为 BD的中点,PO的延长线交 BC于 Q.
(1)求证:OP=OQ;
(2)若 AD=8厘米,AB=6厘米,P从点 A出发,以 1厘米/秒的速度向 D运动(不与 D重合).设点 P运动
时间为 t秒,请用 t表示 PD的长;并求 t为何值时,四边形 PBQD是菱形.
第 5页(共 15页)
25.(12分)已知 O为原点,点 A(8,0)及在第一象限的动点 P(x,y),且 x+y=12,设△OPA的面积为 S.
(1)求 S关于 x的函数解析式;
(2)求 x的取值范围;
(3)当 S=12时,求 P点坐标;
(4)画出函数 S的图象,
26.(12分)如图,在△ABC中,点 O是 AC边上一动点,过点 O作 BC的平行线交∠ACB的角平分线于点 E,交
∠ACB的外角平分线于点 F
(1)求证:EO=FO;
(2)当点 O运动到何处时,四边形 CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若 AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形 ABCE的面积为 .
第 6页(共 15页)
2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(共 10小题,每小题 4分,共 40分)
1.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形又是中心对称图形,符合题意.
故选:D.
2.【解答】解:如图所示,在△ABC中,∠C=90°,则 x+2x=90°.
x=30°.
所以 2x=60°,即∠B为 60°.
故选:D.
3.【解答】解:将点 A(4,2)向左平移 2个单位长度得到点 A′,则点 A′的坐标是(4﹣2,2),即(2,2),
故选:C.
4.【解答】解:由于 3﹣π<0,
∴ 不是二次根式,
故选:A.
5.【解答】解:当 b是斜边时,c= =4,
当 b是直角边时,c= = ,
则 c=4或 ,
故选:D.
6.【解答】解:A、一组对边平行且相等的四边形是平行四边形,故正确;
B、对角线互相垂直且平分的四边形是菱形,故错误;
第 7页(共 15页)
C、对角线相等的菱形是正方形,故正确;
D、对角线相等的平行四边形是矩形,故正确;
故选:B.
7.【解答】解:(1)当 x=2时,y=2,(2,1)不在函数 y= x+1的图象上,(2,0)不在函数 y= x+1的图象上;
(2)当 x=﹣2时,y=0,(﹣2,1)不在函数 y= x+1的图象上,(﹣2,0)在函数 y= x+1的图象上.
故选:D.
8.【解答】解:依题意得 x+2y=60,
即 y= (60﹣x)(0<x<30).
故选:D.
9.【解答】解:根据表格中的数据,得
第④组的频数为 100﹣(4+8+12+24+18+7+3)=24,
其频率为 24:100=0.24.
故选:C.
10.【解答】解:因为 y=﹣x+4的图象经过一、二、四,所以直线 y=x+m与 y=﹣x+4的交点不可能在第三象限,
故选:C.
二.填空题(共 8小题,每小题 4分,共 32分)
11.【解答】解:由题意得,x≥0且 x﹣2≠0,
解得 x≥0且 x≠2.
故答案为:x≥0且 x≠2.
12.【解答】解:设正多边形是 n边形,由题意得
(n﹣2)×180°=144°n.
解得 n=10,
故答案为:十.
13.【解答】解:根据题意,设对角线 AC、BD相交于 O,
则由菱形对角线性质知,AO= AC=3,BO= BD=4,且 AO⊥BO,
∴AB=5,
∴周长 L=4AB=20,
第 8页(共 15页)
∵菱形对角线相互垂直,
∴菱形面积是 S= AC×BD=24.
故答案为 20,24.
14.【解答】解:第 5组到第 7组的频率是 0.125,且容量是 64,那么第 5组到第 7组的频数是 64×0.125=8,
那么第 8组的频数是 64﹣(5+7+11+13+8×3)=4.
故答案为:4.
15.【解答】解:在 Rt△ABC中,AC= =10cm,
∵点 E、F分别是 AO、AD的中点,
∴EF是△AOD的中位线,EF= OD= BD= AC= cm,AF= AD= BC=4cm,AE= AO= AC= cm,
∴△AEF的周长=AE+AF+EF=9cm.
故答案为:9.
16.【解答】解:∵一次函数 y=﹣2x+m的图象经过点 P(﹣2,3),
∴3=4+m,
解得 m=﹣1,
∴y=﹣2x﹣1,
∵当 x=0时,y=﹣1,
∴与 y轴交点 B(0,﹣1),
∵当 y=0时,x=﹣ ,
∴与 x轴交点 A(﹣ ,0),
∴△AOB的面积: ×1× = .
故答案为:
17.【解答】解:∵D是△ABC中 BC边中点,CE⊥AB于 E,BF⊥AC于 F,
∴ED= BC,FD= BC,
∴ED=FD,
又∠EDF=60°,
∴△EDF是等边三角形,
∴ED=FD=EF=4,
∴BC=2ED=8.
第 9页(共 15页)
故答案为 8.
18.【解答】解:第一次折叠如图 1,折痕为 DE,
由折叠得:AE=EC= AC= ×4=2,DE⊥AC
∵∠ACB=90°
∴DE∥BC
∴a=DE= BC= ×3=
第二次折叠如图 2,折痕为 MN,
由折叠得:BN=NC= BC= ×3= ,MN⊥BC
∵∠ACB=90°
∴MN∥AC
∴b=MN= AC= ×4=2
第三次折叠如图 3,折痕为 GH,
由勾股定理得:AB= =5
第 10页(共 15页)
由折叠得:AG=BG= AB= ,GH⊥AB
∴∠AGH=90°
∵∠A=∠A,∠AGH=∠ACB
∴△ACB∽△AGH
∴
∴
∴GH= ,即 c=
∵2> >
∴b>c>a
故答案为:b>c>a
三、解答题(共 8小题,共 78分)
19.【解答】解:(1)
=2﹣1+2+ ﹣1
=2+
(2)
= × ﹣3 ×
=10﹣3×5
=10﹣15
=﹣5
20.【解答】解:如图,设大树高为 AB=10m,
小树高为 CD=4m,
过 C点作 CE⊥AB于 E,则四边形 EBDC是矩形,连接 AC,
∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,
在 Rt△AEC中,AC= = =10m,
故小鸟至少飞行 10m.
第 11页(共 15页)
21.【解答】证明:如图,连接 BD.
∵F,G分别是 BC,CD的中点,
所以 FG∥BD,FG= BD.
∵E,H分别是 AB,DA的中点.
∴EH∥BD,EH= BD.
∴FG∥EH,且 FG=EH.
∴四边形 EFGH是平行四边形.
22.【解答】解:(1)这次调查的总人数为 6÷(36÷360)=60(人);
(2)a=60×0.5=30(人);b=12÷60=0.2;c=6÷60=0.1;d=0.2×60=12(人);
(3)喜爱英语的人数为 1000×0.1=100(人),
由扇形统计图知喜爱语文的人数占总人数的一半,是四个学科中人数最多的科目.
第 12页(共 15页)
23.【解答】解:(1)
根据题意得:A1、B1、C1的坐标分别是:
A1(﹣3,0),B1(2,3),C1(﹣1,4);
(2)S△ABC=S 长方形 ADEF﹣S△ABD﹣S△EBC﹣S△ACF
=4×5﹣ ×3×5﹣ ×3×1﹣ ×2×4
=20﹣ ﹣ ﹣4
=7.
24.【解答】(1)证明:∵四边形 ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
第 13页(共 15页)
又∵O为 BD的中点,
∴OB=OD,
在△POD与△QOB中,
∵
∴△POD≌△QOB(ASA),
∴OP=OQ;
(2)解:PD=8﹣t,
∵四边形 PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形 ABCD是矩形,
∴∠A=90°,
在 Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即 62+t2=(8﹣t)2,
解得:t= ,
即运动时间为 秒时,四边形 PBQD是菱形.
25.【解答】解:(1)∵A和 P点的坐标分别是(8,0)、(x,y),
∴S=0.5×8×y=4y.
∵x+y=12,
∴y=12﹣x.
∴S=4(12﹣x)=48﹣4x,
∴所求的函数关系式为:S=﹣4x+48;
(2)由(1)得 S=﹣4x+48>0,
解得:x<12;
又∵点 P在第一象限,
∴x>0,
综上可得 x的范围为:0<x<12;
第 14页(共 15页)
(3)∵S=12,
∴﹣4x+48=12,
解得 x=9.
∵x+y=12,
∴y=12﹣9=3,
即 P(9,3);
(4)∵解析式为 S=﹣4x+32,
∴函数图象经过点(8,0)(0,32)(但不包括这两点的线段).
所画图象如图
26.【解答】(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,
∵CE平分∠ACB,
∴∠BCE=∠OCE,
∴∠OEC=∠OCE,
∴EO=CO,
同理:FO=CO,
∴EO=FO;
(2)解:当点 O运动到 AC的中点时,四边形 CEAF是矩形;理由如下:
由(1)得:EO=FO,
又∵O是 AC的中点,
第 15页(共 15页)
∴AO=CO,
∴四边形 CEAF是平行四边形,
∵EO=FO=CO,
∴EO=FO=AO=CO,
∴EF=AC,
∴四边形 CEAF是矩形;
(3)解:由(2)得:四边形 CEAF是矩形,
∴∠AEC=90°,
∴AC= = =5,
△ACE的面积= AE×EC= ×3×4=6,
∵122+52=132,
即 AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴△ABC的面积= AB?AC= ×12×5=30,
∴凹四边形 ABCE的面积=△ABC的面积﹣△ACE的面积=30﹣6=24;
故答案为:24.
声
2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷
一、选择题(共 10小题,每小题 4分,共 40分)
1.(4分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(4分)如图所示,在△ABC中,∠C=90°,则∠B为( )
A.15° B.30° C.50° D.60°
3.(4分)将点 A(4,2)向左平移 2个单位长度得到点 A′,则点 A′的坐标是( )
A.(6,2) B.(4,0) C.(2,2) D.(4,4)
4.(4分)下列各式中,不是二次根式的是( )
A. B. C.﹣ D.
5.(4分)在 Rt△ABC中,a=3,b=5,则 c的长为( )
A.2 B. C.4 D.4或
6.(4分)下列说法错误的是( )
A.一组对边平行且相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的菱形是正方形
D.对角线相等的平行四边形是矩形
7.(4分)下面哪个点在函数 y= x+1的图象上( )
A.(2,1) B.(﹣2,1) C.(2,0) D.(﹣2,0)
8.(4分)若等腰三角形的周长为 60cm,底边长为 x cm,一腰长为 y cm,则 y与 x的函数关系式及自变量 x的取值
范围是( )
A.y=60﹣2x(0<x<60) B.y=60﹣2x(0<x<30)
C.y= (60﹣x)(0<x<60) D.y= (60﹣x)(0<x<30)
第 2页(共 15页)
9.(4分)将 100个数据分成①~⑧组,如下表所示:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 4 8 12 24 18 7 3
那么第④组的频率为( )
A.24 B.26 C.0.24 D.0.26
10.(4分)无论 m取任何实数,直线 y=x+m与 y=﹣x+4的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二.填空题(共 8小题,每小题 4分,共 32分)
11.(4分)函数 y= 中自变量 x的取值范围是 .
12.(4分)正多边形的一个内角等于 144°,则该多边形是正 边形.
13.(4分)已知菱形 ABCD中,对角线 AC=6,BD=8,则菱形 ABCD的周长是 ,面积是 .
14.(4分)把容量是 64的样本分成 8组,从第 1组到第 4组的频数分别是 5,7,11,13,第 5组到第 7组的频率
是 0.125,那么第 8组的频数是 .
15.(4分)如图,在矩形 ABCD中,对角线 AC、BD相交于点 O,点 E、F分别是 AO、AD的中点,若 AB=6cm,
BC=8cm,则△AEF的周长= cm.
16.(4分)一次函数 y=﹣2x+m的图象经过点 P(﹣2,3),且与 x轴、y轴分别交于点 A、B,则△AOB的面积等
于 .
17.(4分)如图,D是△ABC中 BC边中点,∠EDF=60°,CE⊥AB于 E,BF⊥AC于 F,若 EF=4,则 BC= .
第 3页(共 15页)
18.(4分)如图,一张三角形纸片 ABC,其中∠C=90°,AC=4,BC=3现小林将纸片做三次折叠:第一次使点
A落在 C处;将纸片展平做第二次折叠,使点 B落在 C处;再将纸片展平做第三次折叠,使点 A落在 B处这三
次折叠的折痕长依次记为 a,b,c,则 a,b,c的大小关系是(从大到小) .
三、解答题(共 8小题,共 78分)
19.(8分)计算:
(1) .
(2) .
20.(8分)有两棵树,一棵高 10米,另一棵高 4米,两树相距 8米,一只小鸟从一棵树的树梢飞到另一棵树的树
梢,问小鸟至少飞行多什么米?
21.(8分)如图,四边形 ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点.
求证:四边形 EFGH是平行四边形.
22.(10分)邵阳县某校为了了解学生对语文(A)、数学(B)、英语(C)、物理(D)四科的喜爱程度(每人只选
第 4页(共 15页)
一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
频数 频率
A a 0.5
B 12 b
C 6 c
D d 0.2
(1)求出这次调查的总人数;
(2)求出表中 a、b、c、d的值;
(3)若该校八年级有学生 1000人,请你算出喜爱英语的人数,并发表你的看法.
23.(10分)如图,△ABC在直角坐标系中,
(1)若把△ABC向上平移 2个单位,再向左平移 1个单位得到△A1B1C1,写出 A1、B1、C1的坐标
(2)求出三角形 ABC的面积.
24.(10分)如图,矩形 ABCD中,点 P是线段 AD上一动点,O为 BD的中点,PO的延长线交 BC于 Q.
(1)求证:OP=OQ;
(2)若 AD=8厘米,AB=6厘米,P从点 A出发,以 1厘米/秒的速度向 D运动(不与 D重合).设点 P运动
时间为 t秒,请用 t表示 PD的长;并求 t为何值时,四边形 PBQD是菱形.
第 5页(共 15页)
25.(12分)已知 O为原点,点 A(8,0)及在第一象限的动点 P(x,y),且 x+y=12,设△OPA的面积为 S.
(1)求 S关于 x的函数解析式;
(2)求 x的取值范围;
(3)当 S=12时,求 P点坐标;
(4)画出函数 S的图象,
26.(12分)如图,在△ABC中,点 O是 AC边上一动点,过点 O作 BC的平行线交∠ACB的角平分线于点 E,交
∠ACB的外角平分线于点 F
(1)求证:EO=FO;
(2)当点 O运动到何处时,四边形 CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若 AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形 ABCE的面积为 .
第 6页(共 15页)
2018-2019学年湖南省怀化市洪江市八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(共 10小题,每小题 4分,共 40分)
1.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形又是中心对称图形,符合题意.
故选:D.
2.【解答】解:如图所示,在△ABC中,∠C=90°,则 x+2x=90°.
x=30°.
所以 2x=60°,即∠B为 60°.
故选:D.
3.【解答】解:将点 A(4,2)向左平移 2个单位长度得到点 A′,则点 A′的坐标是(4﹣2,2),即(2,2),
故选:C.
4.【解答】解:由于 3﹣π<0,
∴ 不是二次根式,
故选:A.
5.【解答】解:当 b是斜边时,c= =4,
当 b是直角边时,c= = ,
则 c=4或 ,
故选:D.
6.【解答】解:A、一组对边平行且相等的四边形是平行四边形,故正确;
B、对角线互相垂直且平分的四边形是菱形,故错误;
第 7页(共 15页)
C、对角线相等的菱形是正方形,故正确;
D、对角线相等的平行四边形是矩形,故正确;
故选:B.
7.【解答】解:(1)当 x=2时,y=2,(2,1)不在函数 y= x+1的图象上,(2,0)不在函数 y= x+1的图象上;
(2)当 x=﹣2时,y=0,(﹣2,1)不在函数 y= x+1的图象上,(﹣2,0)在函数 y= x+1的图象上.
故选:D.
8.【解答】解:依题意得 x+2y=60,
即 y= (60﹣x)(0<x<30).
故选:D.
9.【解答】解:根据表格中的数据,得
第④组的频数为 100﹣(4+8+12+24+18+7+3)=24,
其频率为 24:100=0.24.
故选:C.
10.【解答】解:因为 y=﹣x+4的图象经过一、二、四,所以直线 y=x+m与 y=﹣x+4的交点不可能在第三象限,
故选:C.
二.填空题(共 8小题,每小题 4分,共 32分)
11.【解答】解:由题意得,x≥0且 x﹣2≠0,
解得 x≥0且 x≠2.
故答案为:x≥0且 x≠2.
12.【解答】解:设正多边形是 n边形,由题意得
(n﹣2)×180°=144°n.
解得 n=10,
故答案为:十.
13.【解答】解:根据题意,设对角线 AC、BD相交于 O,
则由菱形对角线性质知,AO= AC=3,BO= BD=4,且 AO⊥BO,
∴AB=5,
∴周长 L=4AB=20,
第 8页(共 15页)
∵菱形对角线相互垂直,
∴菱形面积是 S= AC×BD=24.
故答案为 20,24.
14.【解答】解:第 5组到第 7组的频率是 0.125,且容量是 64,那么第 5组到第 7组的频数是 64×0.125=8,
那么第 8组的频数是 64﹣(5+7+11+13+8×3)=4.
故答案为:4.
15.【解答】解:在 Rt△ABC中,AC= =10cm,
∵点 E、F分别是 AO、AD的中点,
∴EF是△AOD的中位线,EF= OD= BD= AC= cm,AF= AD= BC=4cm,AE= AO= AC= cm,
∴△AEF的周长=AE+AF+EF=9cm.
故答案为:9.
16.【解答】解:∵一次函数 y=﹣2x+m的图象经过点 P(﹣2,3),
∴3=4+m,
解得 m=﹣1,
∴y=﹣2x﹣1,
∵当 x=0时,y=﹣1,
∴与 y轴交点 B(0,﹣1),
∵当 y=0时,x=﹣ ,
∴与 x轴交点 A(﹣ ,0),
∴△AOB的面积: ×1× = .
故答案为:
17.【解答】解:∵D是△ABC中 BC边中点,CE⊥AB于 E,BF⊥AC于 F,
∴ED= BC,FD= BC,
∴ED=FD,
又∠EDF=60°,
∴△EDF是等边三角形,
∴ED=FD=EF=4,
∴BC=2ED=8.
第 9页(共 15页)
故答案为 8.
18.【解答】解:第一次折叠如图 1,折痕为 DE,
由折叠得:AE=EC= AC= ×4=2,DE⊥AC
∵∠ACB=90°
∴DE∥BC
∴a=DE= BC= ×3=
第二次折叠如图 2,折痕为 MN,
由折叠得:BN=NC= BC= ×3= ,MN⊥BC
∵∠ACB=90°
∴MN∥AC
∴b=MN= AC= ×4=2
第三次折叠如图 3,折痕为 GH,
由勾股定理得:AB= =5
第 10页(共 15页)
由折叠得:AG=BG= AB= ,GH⊥AB
∴∠AGH=90°
∵∠A=∠A,∠AGH=∠ACB
∴△ACB∽△AGH
∴
∴
∴GH= ,即 c=
∵2> >
∴b>c>a
故答案为:b>c>a
三、解答题(共 8小题,共 78分)
19.【解答】解:(1)
=2﹣1+2+ ﹣1
=2+
(2)
= × ﹣3 ×
=10﹣3×5
=10﹣15
=﹣5
20.【解答】解:如图,设大树高为 AB=10m,
小树高为 CD=4m,
过 C点作 CE⊥AB于 E,则四边形 EBDC是矩形,连接 AC,
∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,
在 Rt△AEC中,AC= = =10m,
故小鸟至少飞行 10m.
第 11页(共 15页)
21.【解答】证明:如图,连接 BD.
∵F,G分别是 BC,CD的中点,
所以 FG∥BD,FG= BD.
∵E,H分别是 AB,DA的中点.
∴EH∥BD,EH= BD.
∴FG∥EH,且 FG=EH.
∴四边形 EFGH是平行四边形.
22.【解答】解:(1)这次调查的总人数为 6÷(36÷360)=60(人);
(2)a=60×0.5=30(人);b=12÷60=0.2;c=6÷60=0.1;d=0.2×60=12(人);
(3)喜爱英语的人数为 1000×0.1=100(人),
由扇形统计图知喜爱语文的人数占总人数的一半,是四个学科中人数最多的科目.
第 12页(共 15页)
23.【解答】解:(1)
根据题意得:A1、B1、C1的坐标分别是:
A1(﹣3,0),B1(2,3),C1(﹣1,4);
(2)S△ABC=S 长方形 ADEF﹣S△ABD﹣S△EBC﹣S△ACF
=4×5﹣ ×3×5﹣ ×3×1﹣ ×2×4
=20﹣ ﹣ ﹣4
=7.
24.【解答】(1)证明:∵四边形 ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
第 13页(共 15页)
又∵O为 BD的中点,
∴OB=OD,
在△POD与△QOB中,
∵
∴△POD≌△QOB(ASA),
∴OP=OQ;
(2)解:PD=8﹣t,
∵四边形 PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形 ABCD是矩形,
∴∠A=90°,
在 Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即 62+t2=(8﹣t)2,
解得:t= ,
即运动时间为 秒时,四边形 PBQD是菱形.
25.【解答】解:(1)∵A和 P点的坐标分别是(8,0)、(x,y),
∴S=0.5×8×y=4y.
∵x+y=12,
∴y=12﹣x.
∴S=4(12﹣x)=48﹣4x,
∴所求的函数关系式为:S=﹣4x+48;
(2)由(1)得 S=﹣4x+48>0,
解得:x<12;
又∵点 P在第一象限,
∴x>0,
综上可得 x的范围为:0<x<12;
第 14页(共 15页)
(3)∵S=12,
∴﹣4x+48=12,
解得 x=9.
∵x+y=12,
∴y=12﹣9=3,
即 P(9,3);
(4)∵解析式为 S=﹣4x+32,
∴函数图象经过点(8,0)(0,32)(但不包括这两点的线段).
所画图象如图
26.【解答】(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,
∵CE平分∠ACB,
∴∠BCE=∠OCE,
∴∠OEC=∠OCE,
∴EO=CO,
同理:FO=CO,
∴EO=FO;
(2)解:当点 O运动到 AC的中点时,四边形 CEAF是矩形;理由如下:
由(1)得:EO=FO,
又∵O是 AC的中点,
第 15页(共 15页)
∴AO=CO,
∴四边形 CEAF是平行四边形,
∵EO=FO=CO,
∴EO=FO=AO=CO,
∴EF=AC,
∴四边形 CEAF是矩形;
(3)解:由(2)得:四边形 CEAF是矩形,
∴∠AEC=90°,
∴AC= = =5,
△ACE的面积= AE×EC= ×3×4=6,
∵122+52=132,
即 AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴△ABC的面积= AB?AC= ×12×5=30,
∴凹四边形 ABCE的面积=△ABC的面积﹣△ACE的面积=30﹣6=24;
故答案为:24.
声
同课章节目录
