人教版八年级数学上册第11.1.2三角形的高、中线与角平分线 (2)课件(25张ppt)
文档属性
| 名称 | 人教版八年级数学上册第11.1.2三角形的高、中线与角平分线 (2)课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 864.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 00:00:00 | ||
图片预览





文档简介
课件25张PPT。人教版八年级数学上册 11.1 与三角形有关的线段 11.1.2三角形的高、中线与角平分线课件说明 在已学过的过直线外一点作已知直线的垂线、线段的
中点、角的平分线等知识的基础上,本节课学习与三
角形有关的三种重要线段及三角形的稳定性.学习目标:
1.理解三角形的高、中线、角平分线的概念.
2.了解三角形的重心的概念.
3.了解三角形的稳定性.
学习重点:
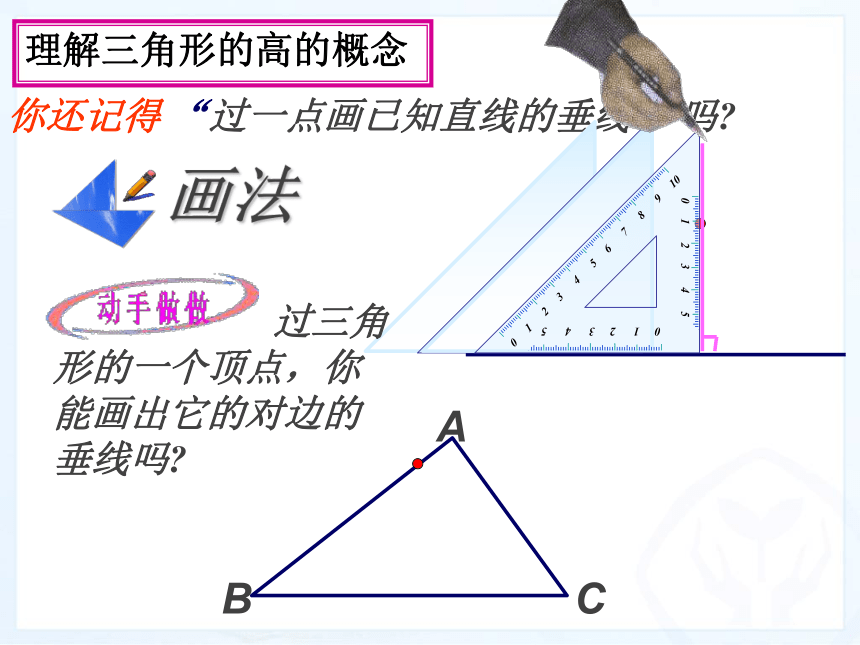
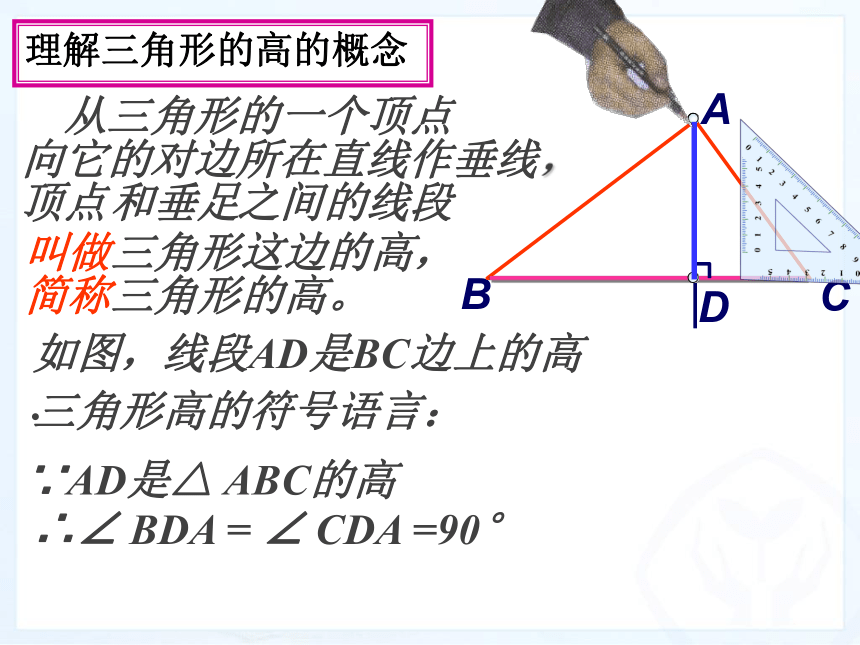
理解三角形的高、中线、角平分线的概念.课件说明你还记得 “过一点画已知直线的垂线” 吗?理解三角形的高的概念A 从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图,线段AD是BC边上的高.三角形高的符号语言:∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°理解三角形的高的概念锐角三角形的三条高 在纸上画一个锐角三角形
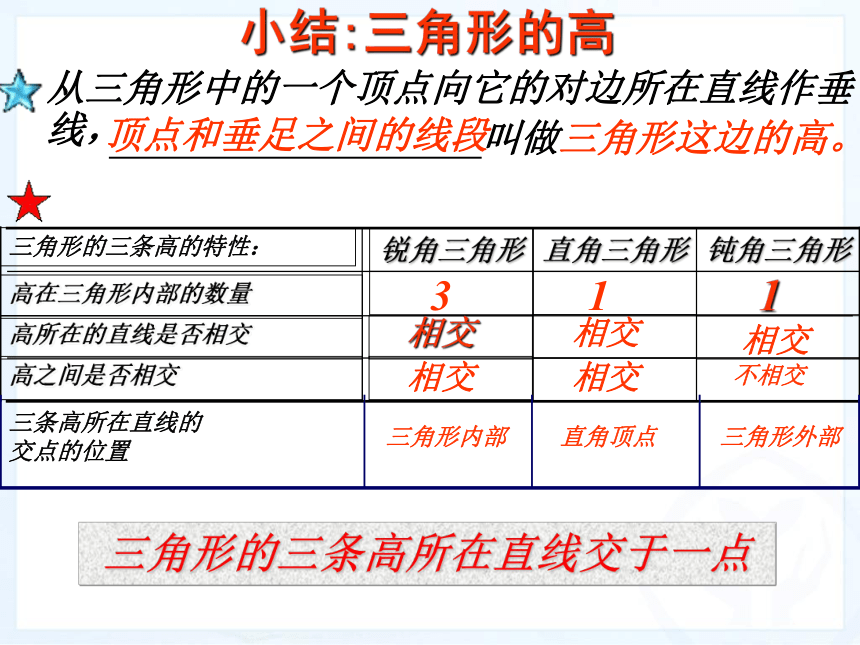
(1)你能画出这个三角形的三条高吗?(2)这三条高之间有怎样的位置关系?将你的结果与同伴进行交流锐角三角形的三条高交于同一点.锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部。ABCDEF直角三角形的三条高在纸上画一个直角三角形将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 ;BD●小结:三角形的高从三角形中的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高。三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三条高所在直线的
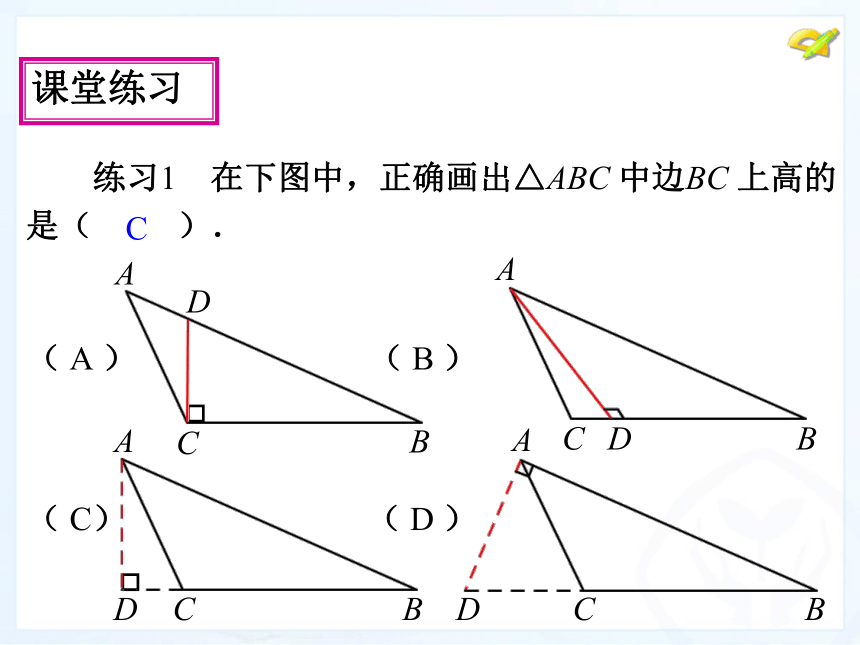
交点的位置三角形内部直角顶点三角形外部C课堂练习 练习1 在下图中,正确画出△ABC 中边BC 上高的
是( ).三角形的中线在三角形中,连结一个顶点和它对边中点的线段叫做这个三角形这边的中线.D∵AD是△ABC的中线∴BD=CD =
任意画一个三角形,然后画出这个三角形三条边的中线,你发现了什么?●●三角形的三条中线相交于一点,交点在三角形的内部.三角形中线的符号语言:EFO理解三角形的中线的概念 问题5 如上页图,画出△ABC 的另两条中线,观
察三条中线,你有什么发现? 三角形的三条中线相交于一点,三角形三条中线的
交点叫做三角形的重心.O22BD6 cm2巩固练习 练习2 如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .理解三角形的角平分线的概念准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.
∠1和∠2 有什么关系?三角形的角平分线ABCD∵AD是 △ ABC的角平分线任意画一个三角形,然后画出这个三角形三个角的角平分线,你发现了什么?●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。●三角形的三条角平分线相交于一点,
交点在三角形的内部︶︶12ACBFEDO∵BE是△ABC的角平分线∴ = _____ =∴∠ACB=2______=2____∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF角平分线的符号语言 三角形的角平分线与角的平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线∠2巩固练习 练习3 如图,AD,BE,CF 是△ABC 的三条角平
分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .∠ABC∠4练一练如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的?ABCDE12FGH①AD是△ABE的角平分线 ( )②BE是△ABD边AD上的中线( )③BE是△ABC边AC上的中线( )④CH是△ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√拓展练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形BD练习拓展AFCDAC∠2 ∠ABC∠4拓展练习CEBC∠CAD∠BAC∠AFC4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°拓展练习5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D拓展练习6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BD=EC D.∠C的对边是DE
C课堂小结(1)本节课学习了哪些主要内容?
(2)你能分别描述三角形中的几种重要线段吗?
(3)你能说说什么是三角形的重心吗?布置作业教科书习题11.1第4、8题.
中点、角的平分线等知识的基础上,本节课学习与三
角形有关的三种重要线段及三角形的稳定性.学习目标:
1.理解三角形的高、中线、角平分线的概念.
2.了解三角形的重心的概念.
3.了解三角形的稳定性.
学习重点:
理解三角形的高、中线、角平分线的概念.课件说明你还记得 “过一点画已知直线的垂线” 吗?理解三角形的高的概念A 从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图,线段AD是BC边上的高.三角形高的符号语言:∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°理解三角形的高的概念锐角三角形的三条高 在纸上画一个锐角三角形
(1)你能画出这个三角形的三条高吗?(2)这三条高之间有怎样的位置关系?将你的结果与同伴进行交流锐角三角形的三条高交于同一点.锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部。ABCDEF直角三角形的三条高在纸上画一个直角三角形将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 ;BD●小结:三角形的高从三角形中的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高。三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三条高所在直线的
交点的位置三角形内部直角顶点三角形外部C课堂练习 练习1 在下图中,正确画出△ABC 中边BC 上高的
是( ).三角形的中线在三角形中,连结一个顶点和它对边中点的线段叫做这个三角形这边的中线.D∵AD是△ABC的中线∴BD=CD =
任意画一个三角形,然后画出这个三角形三条边的中线,你发现了什么?●●三角形的三条中线相交于一点,交点在三角形的内部.三角形中线的符号语言:EFO理解三角形的中线的概念 问题5 如上页图,画出△ABC 的另两条中线,观
察三条中线,你有什么发现? 三角形的三条中线相交于一点,三角形三条中线的
交点叫做三角形的重心.O22BD6 cm2巩固练习 练习2 如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .理解三角形的角平分线的概念准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.
∠1和∠2 有什么关系?三角形的角平分线ABCD∵AD是 △ ABC的角平分线任意画一个三角形,然后画出这个三角形三个角的角平分线,你发现了什么?●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。●三角形的三条角平分线相交于一点,
交点在三角形的内部︶︶12ACBFEDO∵BE是△ABC的角平分线∴ = _____ =∴∠ACB=2______=2____∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF角平分线的符号语言 三角形的角平分线与角的平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线∠2巩固练习 练习3 如图,AD,BE,CF 是△ABC 的三条角平
分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .∠ABC∠4练一练如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的?ABCDE12FGH①AD是△ABE的角平分线 ( )②BE是△ABD边AD上的中线( )③BE是△ABC边AC上的中线( )④CH是△ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√拓展练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形BD练习拓展AFCDAC∠2 ∠ABC∠4拓展练习CEBC∠CAD∠BAC∠AFC4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°拓展练习5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D拓展练习6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BD=EC D.∠C的对边是DE
C课堂小结(1)本节课学习了哪些主要内容?
(2)你能分别描述三角形中的几种重要线段吗?
(3)你能说说什么是三角形的重心吗?布置作业教科书习题11.1第4、8题.
