人教A高中数学必修二4.3.1 空间直角坐标系22张PPT
文档属性
| 名称 | 人教A高中数学必修二4.3.1 空间直角坐标系22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 23:52:25 | ||
图片预览



文档简介
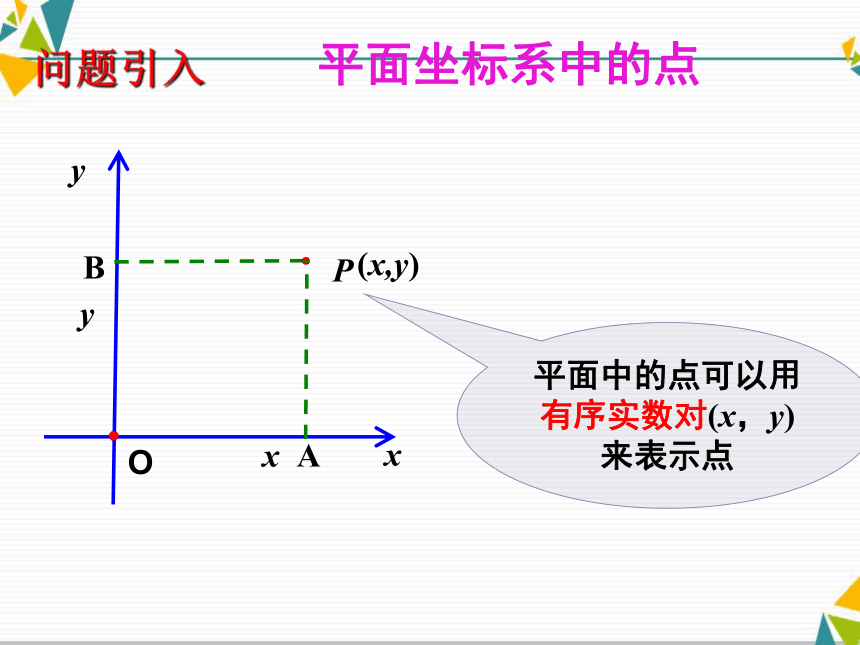
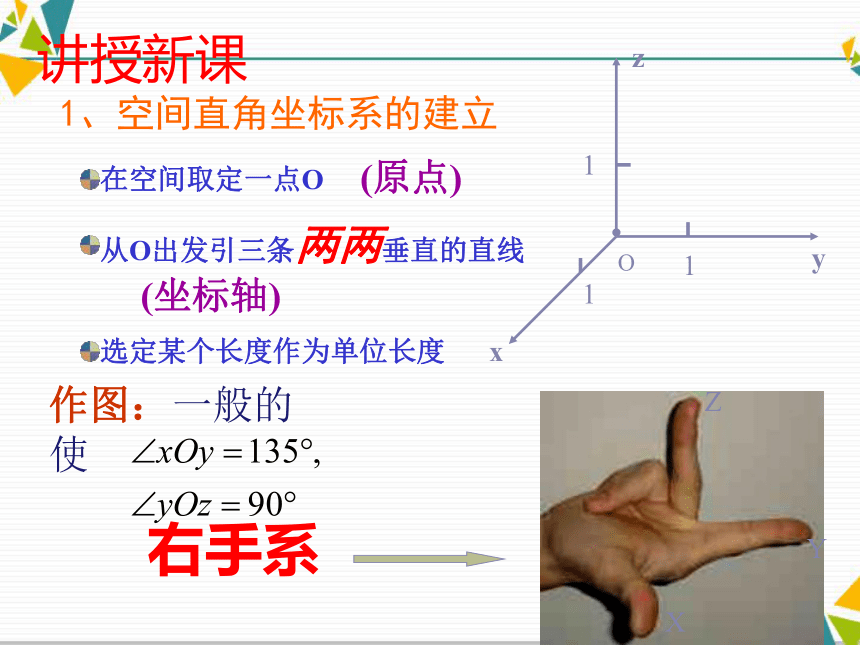
课件22张PPT。空间直角坐标系问题引入问题引入xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示点平面坐标系中的点问题引入AB1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)讲授新课作图: 通过每两个坐标轴的
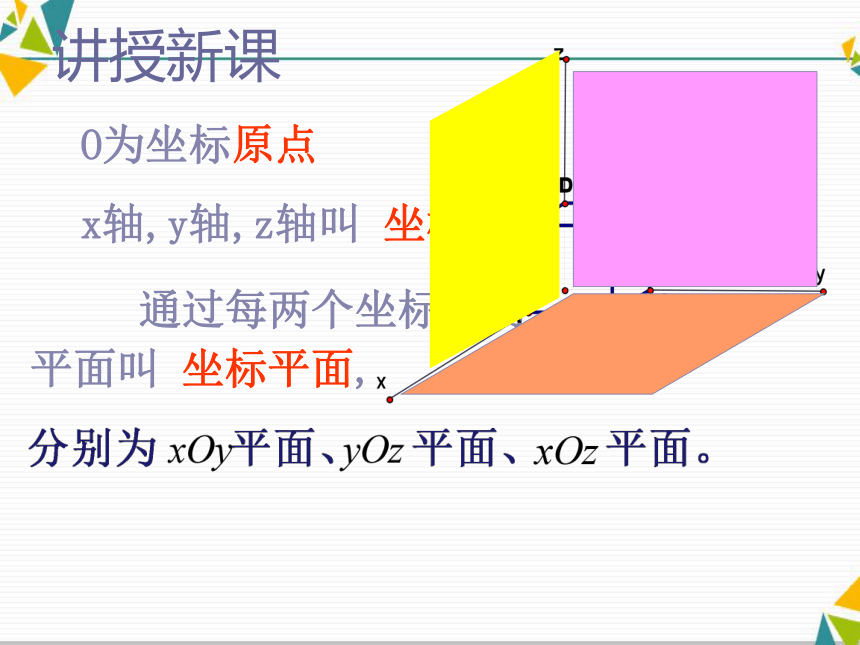
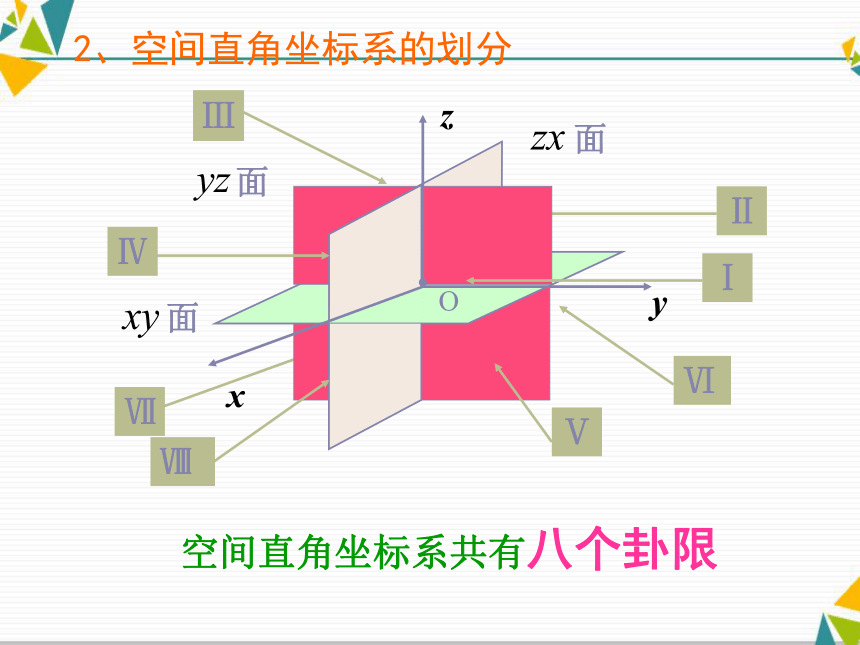
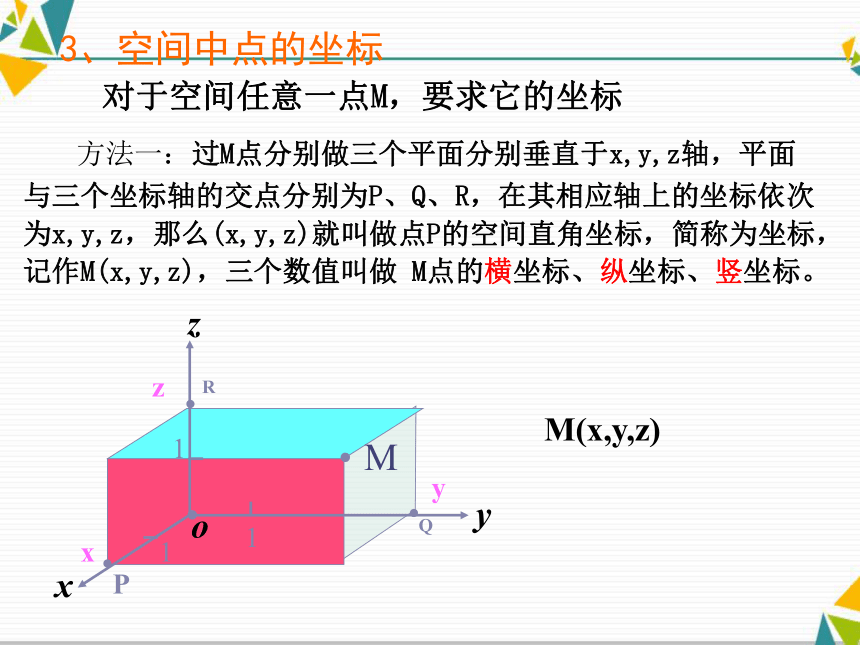
平面叫 坐标平面,讲授新课O为坐标原点x轴,y轴,z轴叫 坐标轴空间直角坐标系共有八个卦限2、空间直角坐标系的划分?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作M(x,y,z),三个数值叫做 M点的横坐标、纵坐标、竖坐标。
M(x,y,z)??P0xyz M点坐标为
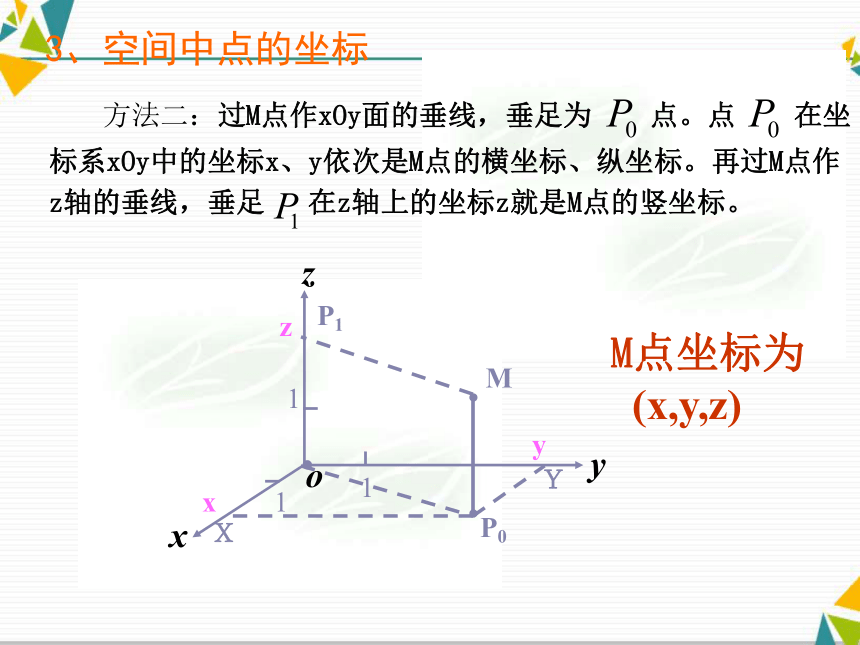
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是M点的横坐标、纵坐标。再过M点作z轴的垂线,垂足 在z轴上的坐标z就是M点的竖坐标。XY 反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.M’O(3,0,2)在xoy平面上的点有哪些?坐标有什么共性?A(3,0,0)
B(3,4,0)
C(0,4,0)
O(0,0,0)(3,0,2)在yoz平面上的点有哪些?坐标有什么共性?(3,0,2)在xoz平面上的点有哪些?坐标有什么共性?x轴上的点的坐标的特点:xOy坐标平面内的点的特点:xOz坐标平面内的点的特点:yOz坐标平面内的点的特点:y轴上的点的坐标的特点:z轴上的点的坐标的特点:P(x,0,0)P(0,y,0)P(0,0,z)P(x,y,0)P(0,y,z)P(x,0,z)规律总结:I(+,+,+),II(-,+,+),III(-,-,+)IV,(+,-,+)
V(+,+,-),VI(-,+,-),VII(-,-,-),VIII(+,-,-)再想一想,各个卦限中点的坐标符号是怎样的?总结:上方卦限Z坐标为正
下方卦限Z坐标为负探究1:关于坐标平面对称点P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)xoz平面对称的点P3为__________;
关于谁对称谁不变(x,y,-z)(-x,y,z)(x, -y, z)探究2:关于坐标轴对称点P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变B设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?空间两点的中点坐标公式你能写出各个面中心的坐标吗?知识小结1.了解空间直角坐标系的概念,学会建立空间直角坐标系(右手系法则).
2.学会用空间直角坐标系表示空间点的坐标.
3.根据点的坐标可以确定与坐标轴对称、坐标平面对称点的坐标。
4、能够通过中点坐标公式求解点的坐标。作业:课本习题第一课时和红对勾相对应课时
平面叫 坐标平面,讲授新课O为坐标原点x轴,y轴,z轴叫 坐标轴空间直角坐标系共有八个卦限2、空间直角坐标系的划分?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作M(x,y,z),三个数值叫做 M点的横坐标、纵坐标、竖坐标。
M(x,y,z)??P0xyz M点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是M点的横坐标、纵坐标。再过M点作z轴的垂线,垂足 在z轴上的坐标z就是M点的竖坐标。XY 反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.M’O(3,0,2)在xoy平面上的点有哪些?坐标有什么共性?A(3,0,0)
B(3,4,0)
C(0,4,0)
O(0,0,0)(3,0,2)在yoz平面上的点有哪些?坐标有什么共性?(3,0,2)在xoz平面上的点有哪些?坐标有什么共性?x轴上的点的坐标的特点:xOy坐标平面内的点的特点:xOz坐标平面内的点的特点:yOz坐标平面内的点的特点:y轴上的点的坐标的特点:z轴上的点的坐标的特点:P(x,0,0)P(0,y,0)P(0,0,z)P(x,y,0)P(0,y,z)P(x,0,z)规律总结:I(+,+,+),II(-,+,+),III(-,-,+)IV,(+,-,+)
V(+,+,-),VI(-,+,-),VII(-,-,-),VIII(+,-,-)再想一想,各个卦限中点的坐标符号是怎样的?总结:上方卦限Z坐标为正
下方卦限Z坐标为负探究1:关于坐标平面对称点P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)xoz平面对称的点P3为__________;
关于谁对称谁不变(x,y,-z)(-x,y,z)(x, -y, z)探究2:关于坐标轴对称点P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变B设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?空间两点的中点坐标公式你能写出各个面中心的坐标吗?知识小结1.了解空间直角坐标系的概念,学会建立空间直角坐标系(右手系法则).
2.学会用空间直角坐标系表示空间点的坐标.
3.根据点的坐标可以确定与坐标轴对称、坐标平面对称点的坐标。
4、能够通过中点坐标公式求解点的坐标。作业:课本习题第一课时和红对勾相对应课时
