人教A高中数学必修二1.1.1 柱、锥、台、球的结构特征24张PPT
文档属性
| 名称 | 人教A高中数学必修二1.1.1 柱、锥、台、球的结构特征24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 23:51:26 | ||
图片预览






文档简介
课件24张PPT。第一章 空间几何体
1.1空间几何体的结构
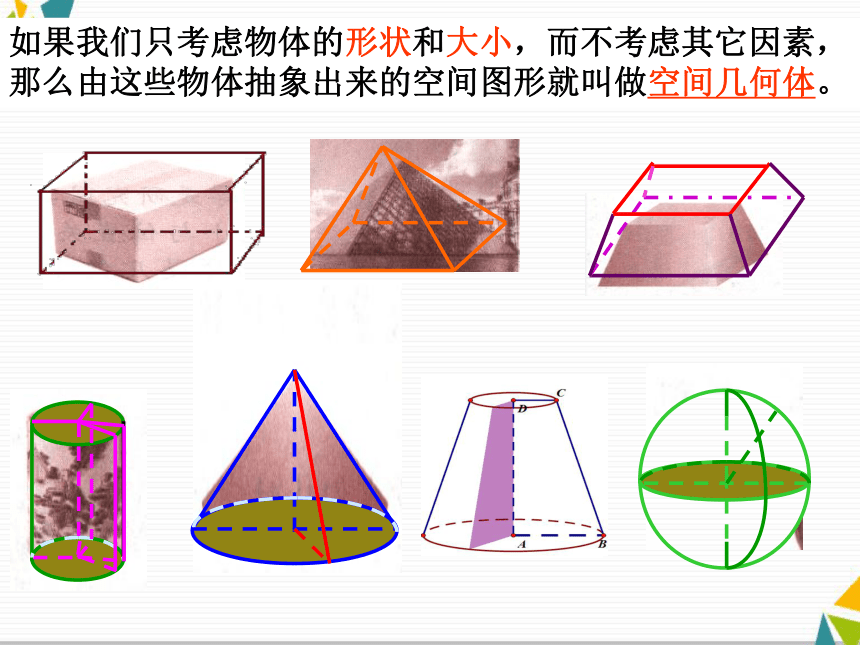
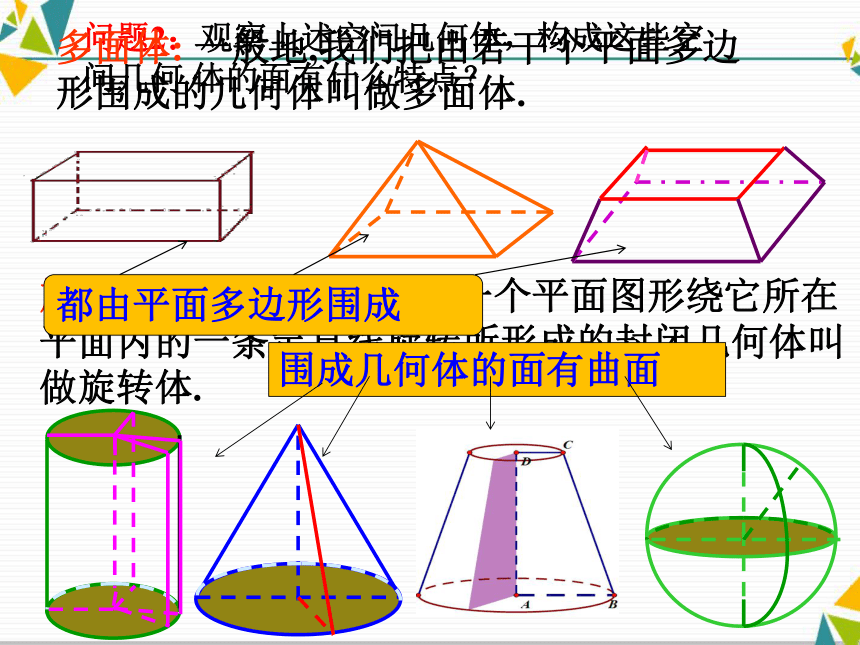
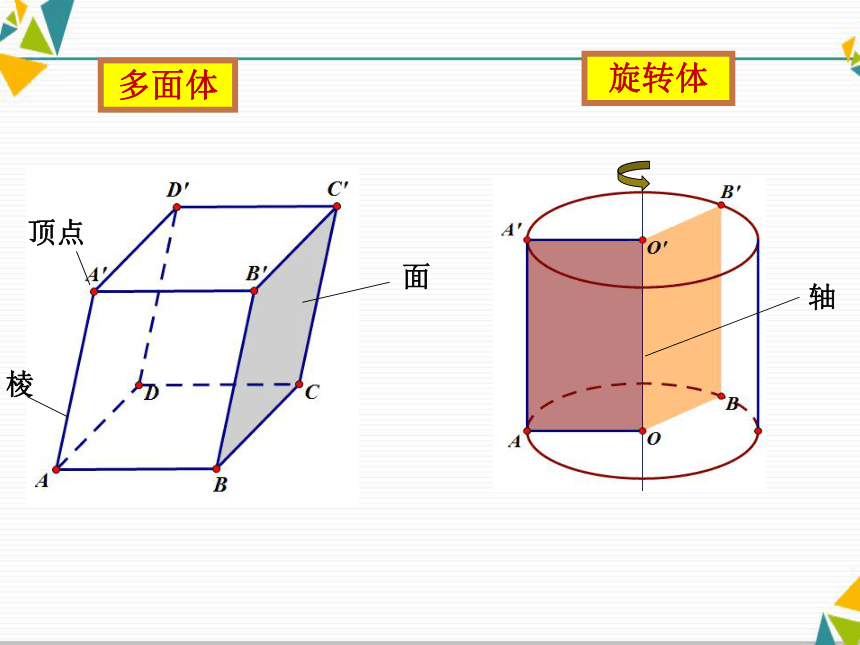
1.1.1柱、锥、台、球的结构特征问题1:观察下面的图片, 这些图片中的物体具有怎样的形状?我们如何描述它们的形状?如果我们只考虑物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。问题2:观察上述空间几何体,构成这些空间几何 体的面有什么特点?多面体: 一般地,我们把由若干个平面多边形围成的几何体叫做多面体.旋转体: 一般地,我们把由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体. 多面体旋转体课堂练习: 下列物体中,哪些具有多面体的形状,哪些具有旋转体的形状?1.1.1柱、锥、台、球的结构特征问题3:观察下列多面体,它们共同的特点是什么?1.定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。棱柱的底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱…… 2.分类:用表示底面各顶点的字母表示棱柱:
棱柱ABCDEF-A'B'C'D'E'F'3.表示:1棱柱的结构特征课堂练习:2. (P 8第1(1)题)下面的几何体中,哪些是棱柱?1、3、53.(P 10第1题)如图,长方体
ABCD-A'B'C'D'
中被截去一部分,其中
EH//A 'D'
截去的几何体是什么?
剩下的几何体是什么?三棱柱五棱柱课堂练习:A'D'B'C'问题4:观察下列多面体,它们共同的特点是什么?SABCDE2棱锥的结构特征3棱台的结构特征问题5:观察左边的几何体,构成它的面有什么特点?与棱锥有何关系?4.(P 9第2题)判断下列几何体是不是棱台,为什么?(1)(2)侧棱不交于一点底面不平行都不是棱台课堂练习:思考:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点OO14、圆柱的结构特征SBOA5、圆锥的结构特征6、圆台的结构特征7、球的结构特征O球心半径AB空间几何体
1.1空间几何体的结构
1.1.1柱、锥、台、球的结构特征问题1:观察下面的图片, 这些图片中的物体具有怎样的形状?我们如何描述它们的形状?如果我们只考虑物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。问题2:观察上述空间几何体,构成这些空间几何 体的面有什么特点?多面体: 一般地,我们把由若干个平面多边形围成的几何体叫做多面体.旋转体: 一般地,我们把由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体. 多面体旋转体课堂练习: 下列物体中,哪些具有多面体的形状,哪些具有旋转体的形状?1.1.1柱、锥、台、球的结构特征问题3:观察下列多面体,它们共同的特点是什么?1.定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。棱柱的底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱…… 2.分类:用表示底面各顶点的字母表示棱柱:
棱柱ABCDEF-A'B'C'D'E'F'3.表示:1棱柱的结构特征课堂练习:2. (P 8第1(1)题)下面的几何体中,哪些是棱柱?1、3、53.(P 10第1题)如图,长方体
ABCD-A'B'C'D'
中被截去一部分,其中
EH//A 'D'
截去的几何体是什么?
剩下的几何体是什么?三棱柱五棱柱课堂练习:A'D'B'C'问题4:观察下列多面体,它们共同的特点是什么?SABCDE2棱锥的结构特征3棱台的结构特征问题5:观察左边的几何体,构成它的面有什么特点?与棱锥有何关系?4.(P 9第2题)判断下列几何体是不是棱台,为什么?(1)(2)侧棱不交于一点底面不平行都不是棱台课堂练习:思考:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点OO14、圆柱的结构特征SBOA5、圆锥的结构特征6、圆台的结构特征7、球的结构特征O球心半径AB空间几何体
