人教A高中数学必修二1.3.2 球的体积和表面积21张PPT
文档属性
| 名称 | 人教A高中数学必修二1.3.2 球的体积和表面积21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 00:00:00 | ||
图片预览








文档简介
课件21张PPT。--球的体积和表面积--探究一:
1、分割越细密,每个圆片越接近什么样的几何体?高是多少?
2、从下往上数第i个“圆片”的半径是多少?体积如何表示?
3、半球的体积与这些小圆片的体积有什么关系?请列式表示。
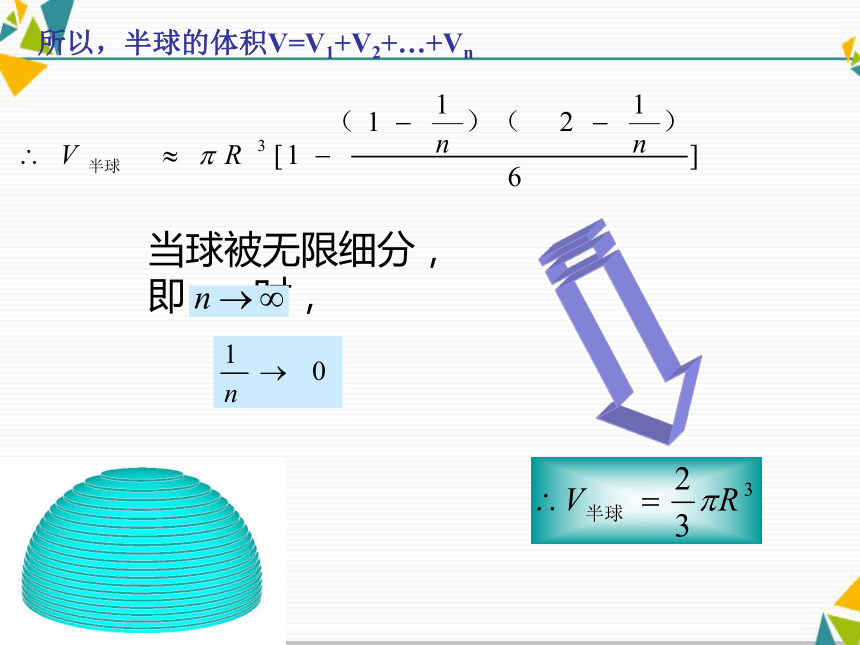
取一个半球,将其切成薄圆片,它的体积就是这些圆片的体积和而且,圆片越多越薄,每个圆片越接近圆柱而且,圆片越多越薄,每个圆片越接近圆柱这些“圆柱”的高是“薄圆片”的厚度从下向上数,第i层“薄圆片”的下底面半径 是 于是,第i层“薄圆片”的体积是所以,半球的体积V=V1+V2+…+Vn所以,半球的体积V=V1+V2+…+Vn想一想无限分割→近似求和→ 准确求和,以及当n→∞时,1/n→0是我们数学中“无限逼近”的重要思想
球的表面积探究二:
1、经线圈和纬线圈将球面分割成n片,每一片的顶点和球心的连线构成的几何体接近什么几何体?
2、分割越细密即n越大,每个几何体的体积可以近似的用什么样的几何体求体积?请列式表示出来。
3、球的体积又可以如何表示?推导出球的表面积公式。球的表面积第一步:分割球面被分割成n个网格,表面积分别为:则球的表面积:则球的体积为:球的表面积第二步:求近似和由第一步得:球的表面积第三步:化为准确和 如果网格分的越细,则: “小锥体”就越接近小棱锥球的表面积例:如图:圆柱的底面直径与高都等于球的直径。
求证:(1)球的体积等于圆柱体积的
(2)球的表面积等于圆柱的全面积的在圆柱容球中,
球的体积是圆柱体积的 2/3?? ,
球的表面积也是圆柱全面积的2/3 ??。? 这是我生平最得意的 定理 嗨!如何推导锥体的体积公式啊,我要灌水!咳咳,
幂势即同,
积不容异 当然没有!是高度,和每一张纸的面积!夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等。夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等。底面半径和高都为R的圆柱半径为R的半球谢谢大家,再见!
1、分割越细密,每个圆片越接近什么样的几何体?高是多少?
2、从下往上数第i个“圆片”的半径是多少?体积如何表示?
3、半球的体积与这些小圆片的体积有什么关系?请列式表示。
取一个半球,将其切成薄圆片,它的体积就是这些圆片的体积和而且,圆片越多越薄,每个圆片越接近圆柱而且,圆片越多越薄,每个圆片越接近圆柱这些“圆柱”的高是“薄圆片”的厚度从下向上数,第i层“薄圆片”的下底面半径 是 于是,第i层“薄圆片”的体积是所以,半球的体积V=V1+V2+…+Vn所以,半球的体积V=V1+V2+…+Vn想一想无限分割→近似求和→ 准确求和,以及当n→∞时,1/n→0是我们数学中“无限逼近”的重要思想
球的表面积探究二:
1、经线圈和纬线圈将球面分割成n片,每一片的顶点和球心的连线构成的几何体接近什么几何体?
2、分割越细密即n越大,每个几何体的体积可以近似的用什么样的几何体求体积?请列式表示出来。
3、球的体积又可以如何表示?推导出球的表面积公式。球的表面积第一步:分割球面被分割成n个网格,表面积分别为:则球的表面积:则球的体积为:球的表面积第二步:求近似和由第一步得:球的表面积第三步:化为准确和 如果网格分的越细,则: “小锥体”就越接近小棱锥球的表面积例:如图:圆柱的底面直径与高都等于球的直径。
求证:(1)球的体积等于圆柱体积的
(2)球的表面积等于圆柱的全面积的在圆柱容球中,
球的体积是圆柱体积的 2/3?? ,
球的表面积也是圆柱全面积的2/3 ??。? 这是我生平最得意的 定理 嗨!如何推导锥体的体积公式啊,我要灌水!咳咳,
幂势即同,
积不容异 当然没有!是高度,和每一张纸的面积!夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等。夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等。底面半径和高都为R的圆柱半径为R的半球谢谢大家,再见!
