人教A高中数学必修二2.1.1 平面:21张PPT
文档属性
| 名称 | 人教A高中数学必修二2.1.1 平面:21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 486.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 00:00:00 | ||
图片预览






文档简介
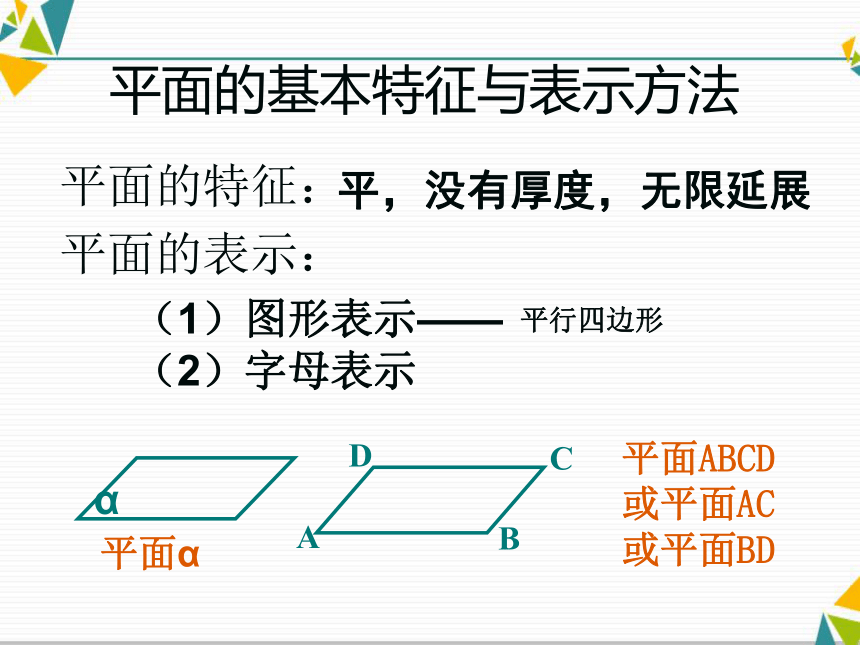
课件21张PPT。§2.1.1平面平面的基本特征与表示方法平面的特征:平,没有厚度,无限延展平面的表示:(1)图形表示——
(2)字母表示下列命题正确的是( ) A.画一个平面,使它的长为 14 cm,宽为 5 cm
B.一个平面的面积可以是 16 m2
C.平面内的一条直线把这个平面分成两部分,一个平面把空间分成两部分
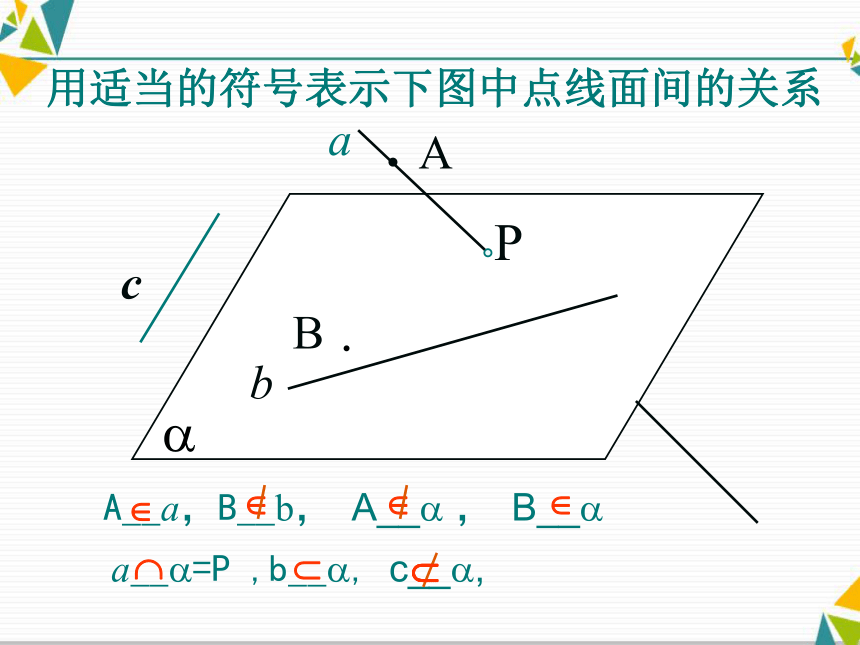
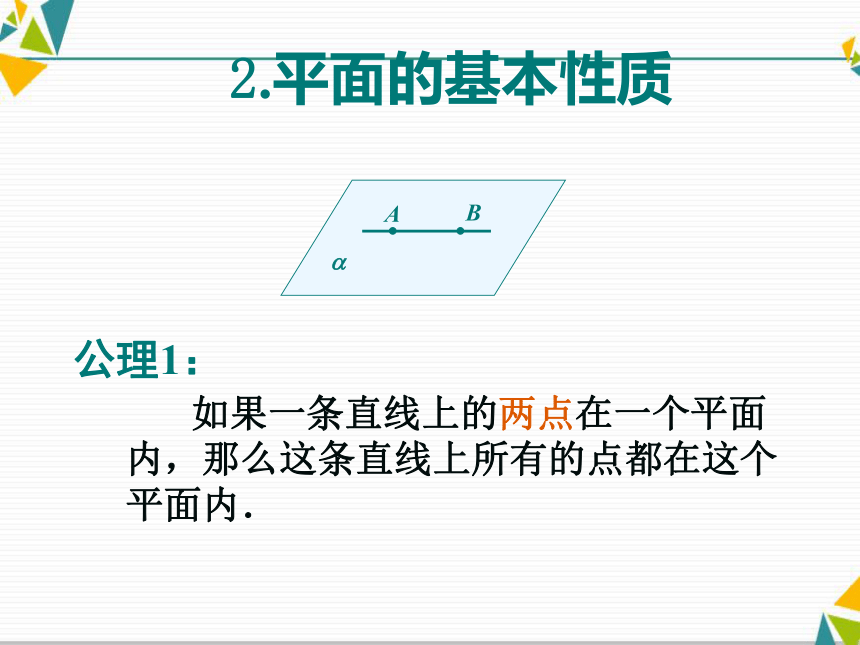
D.10 个平面重叠起来,要比 2 个平面重叠起来厚适应练习用适当的符号表示下图中点线面间的关系 A__a,B__b, A__? , B__? a__?=P ,b__?, c__?,???? 探究一: 想一想,为什么衣帽架需要两端各有一个螺丝才能把它固定在墙上,只固定一端行不行?2.平面的基本性质 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 2.平面的基本性质A?B公理1: 探究二: 为什么照相机的支架设计为三脚架? 为什么四条腿的椅子在地面不平时会出现晃动,三条腿的凳子呢?2.平面的基本性质观察自行车梯的设计你会得到什么启示?2.平面的基本性质 公理2 过不在同一直线上的三点,有
且只有一个平面.BCA2.平面的基本性质思考: 一条直线和直线外一点能点确定一个平面吗?
两条相交直线能确定一个平面吗?
两条平行直线能确定一个平面吗?推论:1、一条直线和直线外一点能确定一个平面;
2、两条相交直线能确定一个平面;
3、两条平行直线能确定一个平面。探究三:
思考1:如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的
平面是否只相交于一点B?为什么?思考2:如果两条不重合
的直线有公共点,则其
公共点只有一个。如果两个不重合的平面有公共点,其公共点有多少个?这些公共点的位置关系如何?2.平面的基本性质2.平面的基本性质公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线. (1) 经过三点确定一个平面.( )
(2) 经过两两相交的三条直线确定一个平面.
(3) 若点A∈直线a,点A∈平面?,则a??.
(4) 平面?与平面?相交,它们只有有限个
公共点.判断下列命题是否正确:( )( )( )适应练习例题分析 正方体ABCD-A1B1C1D1中,底面中心为O,
判断下列命题是否正确,并说明理由。
(1)直线A1C在平面A1BCC1内
(2)直线A1C在平面B1BCC1内
(3)A、O、C三点确定一个平面
(4)A1、B、C确定平面A1BCD1
(5)A1、B、D、D1四点共面例2.如右图在四面体中,若直线EH和FG相交于K,则K点在BD上吗,为什么? P例题分析K 例3.如右图,在正方体ABCD-A’B’C’D’中,
(1)在图中作出平面 ACC’A’
与底面BB’D’D的交线.
(2)在图中作出平面 ACC’A’
与平面DBC’的交线.例题分析巩固训练练习1. 如图,用符号表示下列图形中点、直线、平面之间的位置关系. 1) A__?,B__?,?__?=l,a??=__,a?__=B2) a__?,b__?,???=__,a__l=P,b?l=__,__?__=P???A??l?Pab?练习2.已知△ABC在平面?外,它的三边所在直线分别交?于P,Q,R则P,Q,R三点是否共线,为什么?
?PRQ巩固训练如右图,在正方体ABCD-A’B’C’D’中,
在图中作出平面 DBB’D’与
平面ABC’D’的交线.
在图中作出平面 ACD’与
平面DBC’的交线.巩固训练1.平面的概念;2.平面的画法、表示方法及两个平面相交的画法;3.三条公理推论1、推论2、推论3、课堂小结课后作业1.课本24-25页练习1,4,5,6,7题.2.如图,点P是正方体ABCD-A1B1C1D1的棱AB的中点,试画出由D1,C,P三点所确定的平面?与长方体表面的交线.P
(2)字母表示下列命题正确的是( ) A.画一个平面,使它的长为 14 cm,宽为 5 cm
B.一个平面的面积可以是 16 m2
C.平面内的一条直线把这个平面分成两部分,一个平面把空间分成两部分
D.10 个平面重叠起来,要比 2 个平面重叠起来厚适应练习用适当的符号表示下图中点线面间的关系 A__a,B__b, A__? , B__? a__?=P ,b__?, c__?,???? 探究一: 想一想,为什么衣帽架需要两端各有一个螺丝才能把它固定在墙上,只固定一端行不行?2.平面的基本性质 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 2.平面的基本性质A?B公理1: 探究二: 为什么照相机的支架设计为三脚架? 为什么四条腿的椅子在地面不平时会出现晃动,三条腿的凳子呢?2.平面的基本性质观察自行车梯的设计你会得到什么启示?2.平面的基本性质 公理2 过不在同一直线上的三点,有
且只有一个平面.BCA2.平面的基本性质思考: 一条直线和直线外一点能点确定一个平面吗?
两条相交直线能确定一个平面吗?
两条平行直线能确定一个平面吗?推论:1、一条直线和直线外一点能确定一个平面;
2、两条相交直线能确定一个平面;
3、两条平行直线能确定一个平面。探究三:
思考1:如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的
平面是否只相交于一点B?为什么?思考2:如果两条不重合
的直线有公共点,则其
公共点只有一个。如果两个不重合的平面有公共点,其公共点有多少个?这些公共点的位置关系如何?2.平面的基本性质2.平面的基本性质公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线. (1) 经过三点确定一个平面.( )
(2) 经过两两相交的三条直线确定一个平面.
(3) 若点A∈直线a,点A∈平面?,则a??.
(4) 平面?与平面?相交,它们只有有限个
公共点.判断下列命题是否正确:( )( )( )适应练习例题分析 正方体ABCD-A1B1C1D1中,底面中心为O,
判断下列命题是否正确,并说明理由。
(1)直线A1C在平面A1BCC1内
(2)直线A1C在平面B1BCC1内
(3)A、O、C三点确定一个平面
(4)A1、B、C确定平面A1BCD1
(5)A1、B、D、D1四点共面例2.如右图在四面体中,若直线EH和FG相交于K,则K点在BD上吗,为什么? P例题分析K 例3.如右图,在正方体ABCD-A’B’C’D’中,
(1)在图中作出平面 ACC’A’
与底面BB’D’D的交线.
(2)在图中作出平面 ACC’A’
与平面DBC’的交线.例题分析巩固训练练习1. 如图,用符号表示下列图形中点、直线、平面之间的位置关系. 1) A__?,B__?,?__?=l,a??=__,a?__=B2) a__?,b__?,???=__,a__l=P,b?l=__,__?__=P???A??l?Pab?练习2.已知△ABC在平面?外,它的三边所在直线分别交?于P,Q,R则P,Q,R三点是否共线,为什么?
?PRQ巩固训练如右图,在正方体ABCD-A’B’C’D’中,
在图中作出平面 DBB’D’与
平面ABC’D’的交线.
在图中作出平面 ACD’与
平面DBC’的交线.巩固训练1.平面的概念;2.平面的画法、表示方法及两个平面相交的画法;3.三条公理推论1、推论2、推论3、课堂小结课后作业1.课本24-25页练习1,4,5,6,7题.2.如图,点P是正方体ABCD-A1B1C1D1的棱AB的中点,试画出由D1,C,P三点所确定的平面?与长方体表面的交线.P
