人教A高中数学必修二2.2 直线与平面平行的性质15张PPT
文档属性
| 名称 | 人教A高中数学必修二2.2 直线与平面平行的性质15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 251.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 00:00:00 | ||
图片预览




文档简介
课件15张PPT。 2.2.3 直线与平面平行的性质3.直线与平面平行的判定方法:⑴定义法:直线与平面没有公共点⑵判定定理.1.直线与直线的位置关系有共面异面平行相交复习回顾:2.直线与平面的位置关系有:直线在平面内,直线与平面相交,直线与平面平行
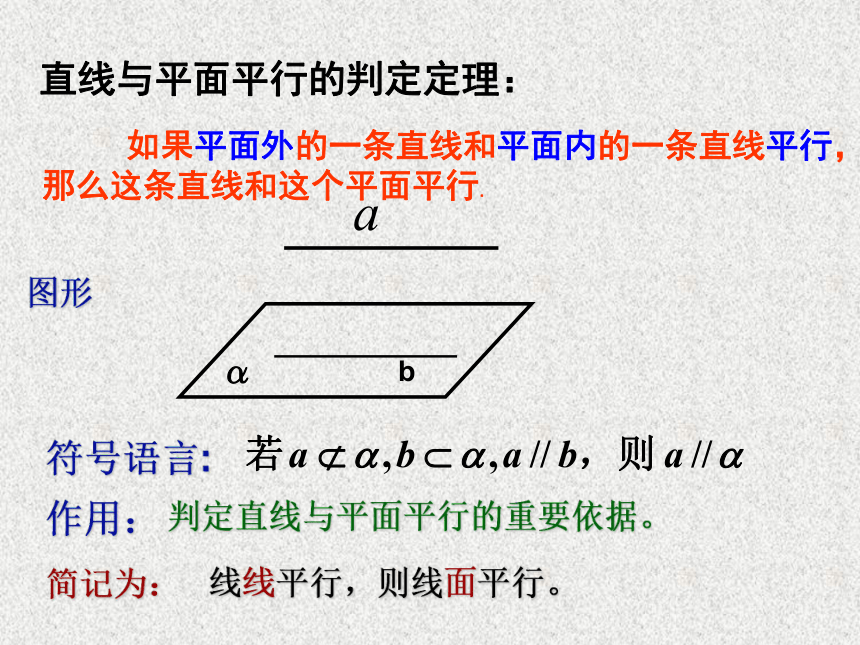
如果平面外的一条直线和平面内的一条直线平行,
那么这条直线和这个平面平行.简记为:线线平行,则线面平行。判定直线与平面平行的重要依据。图形作用:符号语言:直线与平面平行的判定定理:(1)如果一条直线和一个平面平行,那么这条
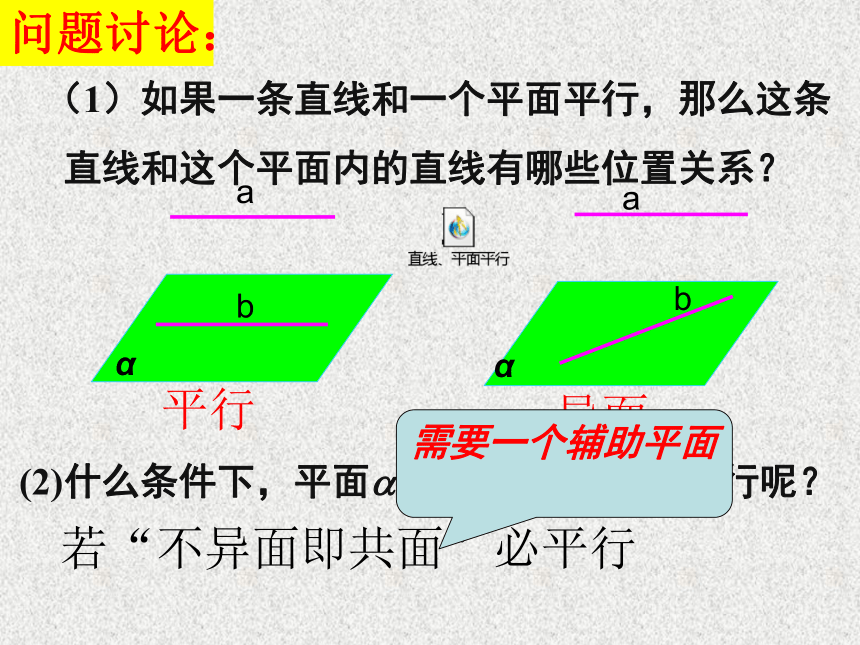
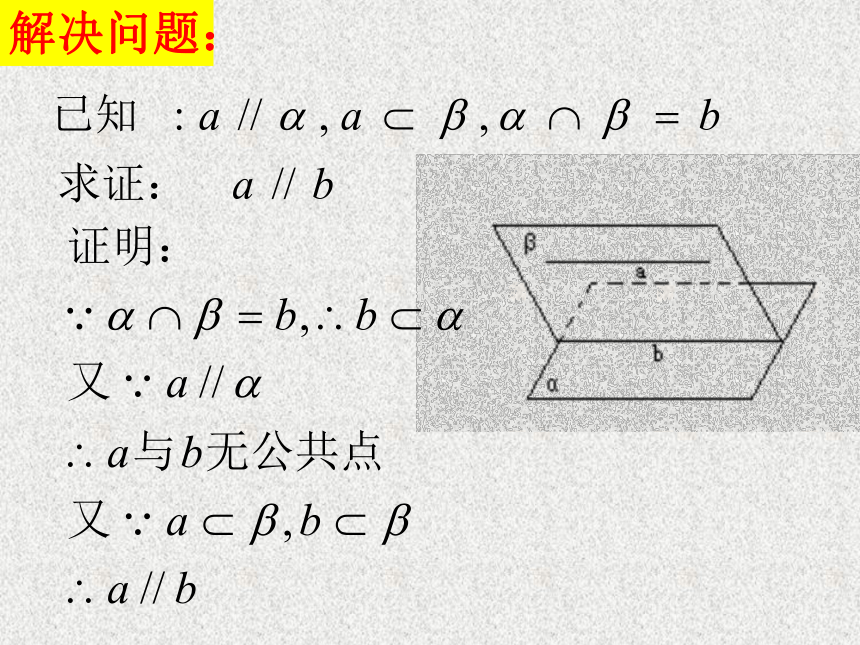
直线和这个平面内的直线有哪些位置关系? 问题讨论:平行异面(2)什么条件下,平面?内的直线与直线a平行呢?需要一个辅助平面解决问题:线面平行的性质定理: 一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。讲授新课:作用:判定直线与直线平行的重要依据。关键:寻找平面与平面的交线。简记为:“线面平行,则线线平行”( )( )( )练习1:判断下列命题是否正确?(1)若直线a与平面?平行,则a与?内任一直线平行. ( )例1.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.例1.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.abc线面平行线线平行线面平行 例2 如图所示的一块木料中,棱BC平行于面A'C'.过点P作直EF//B'C',棱A'B'、C'D'于点E、F,连结BE、CF,FPE解:⑴如图,在平面A'C'内, 下面证明EF、BE、
CF为应画的线.分别交⑴要经过面A'C'内的一点P和棱BC 将木料锯开,应怎样画线?⑴则EF、BE、CF为应画的线.BC//B'C'EF//B'C'BC//EFEF、BE、CF共面. 例2 如图所示的一块木料中,棱BC平行于面A'C'.证明:FPE⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线? 例2 如图所示的一块木料中,棱BC平行于面A'C'.⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?⑵所画的线与平面AC是什么位置关系?⑵解:EF//面AC由⑴,得BE、CF都与面AC相交.EF//BC,EF//BC线面平行线线平行线面平行练习2.ABCD是平行四边形,点P是平面
ABCD外一点,M是PC的中点,在DM
上取一点G,过G和AP作平面交平面
BDM于GH.
求证:AP//GHPABCDMGHO提示:连结AC交BD于O,连结OM⑴判定定理.线线平行线面平行⑵性质定理.线面平行线线平行1.直线与平面平行的性质定理2.判定定理与性质定理展示的数学思想方法:3.要注意判定定理与性质定理的综合运用a∥b.性质定理的运用.课堂小结:书面作业:课本第62页 第6题
如果平面外的一条直线和平面内的一条直线平行,
那么这条直线和这个平面平行.简记为:线线平行,则线面平行。判定直线与平面平行的重要依据。图形作用:符号语言:直线与平面平行的判定定理:(1)如果一条直线和一个平面平行,那么这条
直线和这个平面内的直线有哪些位置关系? 问题讨论:平行异面(2)什么条件下,平面?内的直线与直线a平行呢?需要一个辅助平面解决问题:线面平行的性质定理: 一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。讲授新课:作用:判定直线与直线平行的重要依据。关键:寻找平面与平面的交线。简记为:“线面平行,则线线平行”( )( )( )练习1:判断下列命题是否正确?(1)若直线a与平面?平行,则a与?内任一直线平行. ( )例1.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.例1.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.abc线面平行线线平行线面平行 例2 如图所示的一块木料中,棱BC平行于面A'C'.过点P作直EF//B'C',棱A'B'、C'D'于点E、F,连结BE、CF,FPE解:⑴如图,在平面A'C'内, 下面证明EF、BE、
CF为应画的线.分别交⑴要经过面A'C'内的一点P和棱BC 将木料锯开,应怎样画线?⑴则EF、BE、CF为应画的线.BC//B'C'EF//B'C'BC//EFEF、BE、CF共面. 例2 如图所示的一块木料中,棱BC平行于面A'C'.证明:FPE⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线? 例2 如图所示的一块木料中,棱BC平行于面A'C'.⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?⑵所画的线与平面AC是什么位置关系?⑵解:EF//面AC由⑴,得BE、CF都与面AC相交.EF//BC,EF//BC线面平行线线平行线面平行练习2.ABCD是平行四边形,点P是平面
ABCD外一点,M是PC的中点,在DM
上取一点G,过G和AP作平面交平面
BDM于GH.
求证:AP//GHPABCDMGHO提示:连结AC交BD于O,连结OM⑴判定定理.线线平行线面平行⑵性质定理.线面平行线线平行1.直线与平面平行的性质定理2.判定定理与性质定理展示的数学思想方法:3.要注意判定定理与性质定理的综合运用a∥b.性质定理的运用.课堂小结:书面作业:课本第62页 第6题
