人教A高中数学必修二2.2.2 平面与平面平行的判定18张PPT
文档属性
| 名称 | 人教A高中数学必修二2.2.2 平面与平面平行的判定18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 718.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 23:56:20 | ||
图片预览




文档简介
课件18张PPT。平面与平面
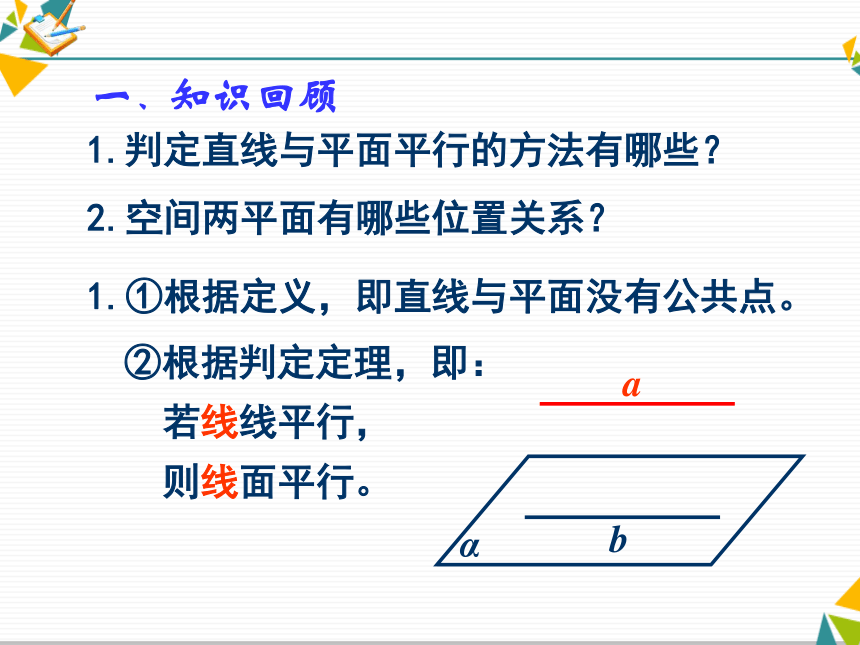
平行的判定②根据判定定理,即:
若线线平行,
则线面平行。一、知识回顾2.空间两平面有哪些位置关系?1.判定直线与平面平行的方法有哪些?abα1.①根据定义,即直线与平面没有公共点。一、知识回顾2.空间两平面有哪些位置关系?1.判定直线与平面平行的方法有哪些?相交平行有公共无数点
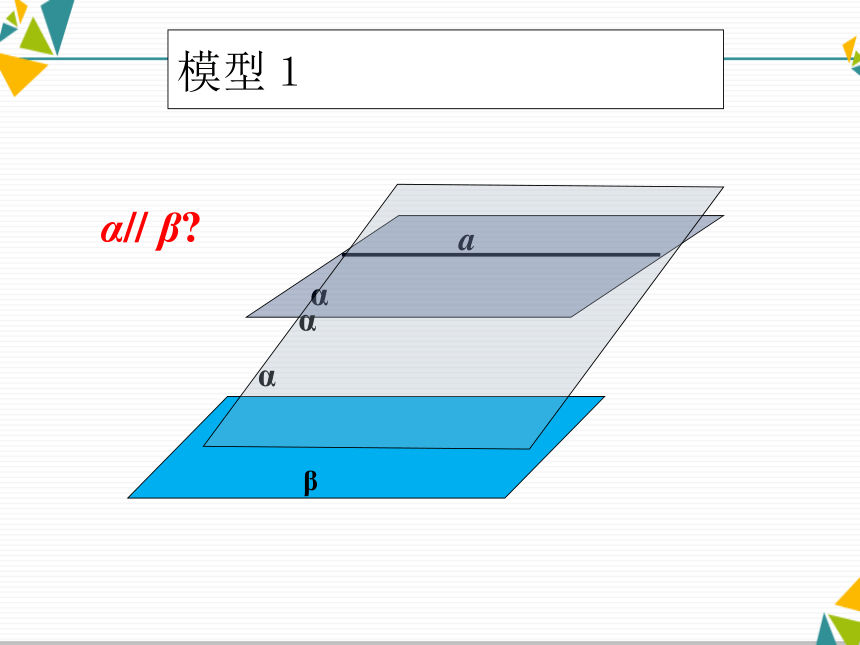
(构成一条直线)无公共点思考:反之,若α中所有直线都平行β ,则α∥β启示? 两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。若平面α∥β,则α中所有直线都平行β二、新知探究??;!模型1αβα// β?αα平面α内有一条直线 a 平行平面β,
则α∥ β 吗? 请举例说明。问题1问题2平面α内有两条直线 a , b 平行平面
β, 则α∥ β 吗? 请举例说明。合作探究:二、新知探究
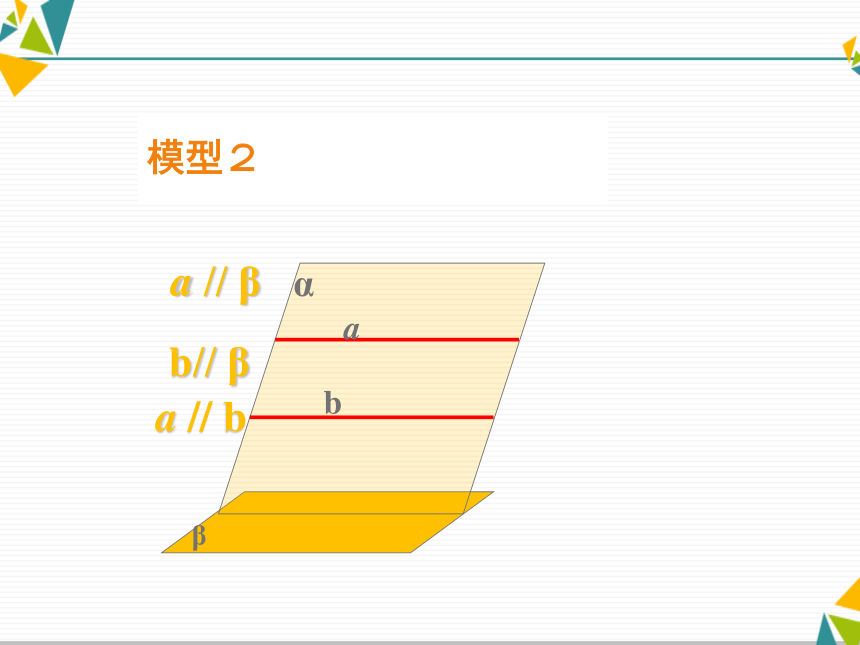
模型2a // βabαb// ββa // b当三角板ABC的两条边BC、AB都平行桌面α时,ABC所在的平面是否平行桌面α?动手体验模型
验证你能得到什么结论abαβ两个平面平行的判定 判定定理:如果一个平面内有 都 于另一个平面,那么这两个平面平行. 图形语言:符号语言:相交直线两条平行三、例题解析例 1: 判断下列结论是否正确:1.若m?α, n?α, m∥β, n∥β, 则α∥β2.若α内任意直线都平行于β, 则α∥β如果两个平面分别经过两条平行线中的一条,
那么这两个平面 ( )
A.平行. B.相交.
C.重合. D.平行或相交.3.DD1DCBAC1B1A1例 2: 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点,
求证:平面PQR∥平面C1BD.RQP变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点
求证:平面PQR∥平面C1BD.D1RQDCBAC1B1A1P例 2: 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.练习×√×√平行或者异面小 结1.通过本节课的学习,你学会了
哪些判定面面平行的方法?2.上述判定面面平行的方法体
现了什么思想?平面与平面平行的判定方法:2.数学思想转化①定义;②判定定理;1.知识内容小 结62练习:7,8作业
若线线平行,
则线面平行。一、知识回顾2.空间两平面有哪些位置关系?1.判定直线与平面平行的方法有哪些?abα1.①根据定义,即直线与平面没有公共点。一、知识回顾2.空间两平面有哪些位置关系?1.判定直线与平面平行的方法有哪些?相交平行有公共无数点
(构成一条直线)无公共点思考:反之,若α中所有直线都平行β ,则α∥β启示? 两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。若平面α∥β,则α中所有直线都平行β二、新知探究??;!模型1αβα// β?αα平面α内有一条直线 a 平行平面β,
则α∥ β 吗? 请举例说明。问题1问题2平面α内有两条直线 a , b 平行平面
β, 则α∥ β 吗? 请举例说明。合作探究:二、新知探究
模型2a // βabαb// ββa // b当三角板ABC的两条边BC、AB都平行桌面α时,ABC所在的平面是否平行桌面α?动手体验模型
验证你能得到什么结论abαβ两个平面平行的判定 判定定理:如果一个平面内有 都 于另一个平面,那么这两个平面平行. 图形语言:符号语言:相交直线两条平行三、例题解析例 1: 判断下列结论是否正确:1.若m?α, n?α, m∥β, n∥β, 则α∥β2.若α内任意直线都平行于β, 则α∥β如果两个平面分别经过两条平行线中的一条,
那么这两个平面 ( )
A.平行. B.相交.
C.重合. D.平行或相交.3.DD1DCBAC1B1A1例 2: 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点,
求证:平面PQR∥平面C1BD.RQP变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点
求证:平面PQR∥平面C1BD.D1RQDCBAC1B1A1P例 2: 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.练习×√×√平行或者异面小 结1.通过本节课的学习,你学会了
哪些判定面面平行的方法?2.上述判定面面平行的方法体
现了什么思想?平面与平面平行的判定方法:2.数学思想转化①定义;②判定定理;1.知识内容小 结62练习:7,8作业
