2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷(pdf解析版)
文档属性
| 名称 | 2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷(pdf解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 565.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-01 20:59:29 | ||
图片预览



文档简介
第 1页(共 15页)
2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷
一.选择题(共 10小题,每小题 4分共 40分)
1.(4分)下列交通标志图案中,是中心对称图形的是( )
A. B. C. D.
2.(4分)在实际生活中,我们经常利用一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )
A. 电动伸缩门 B. 升降台
C. 栅栏 D. 窗户
3.(4分)平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
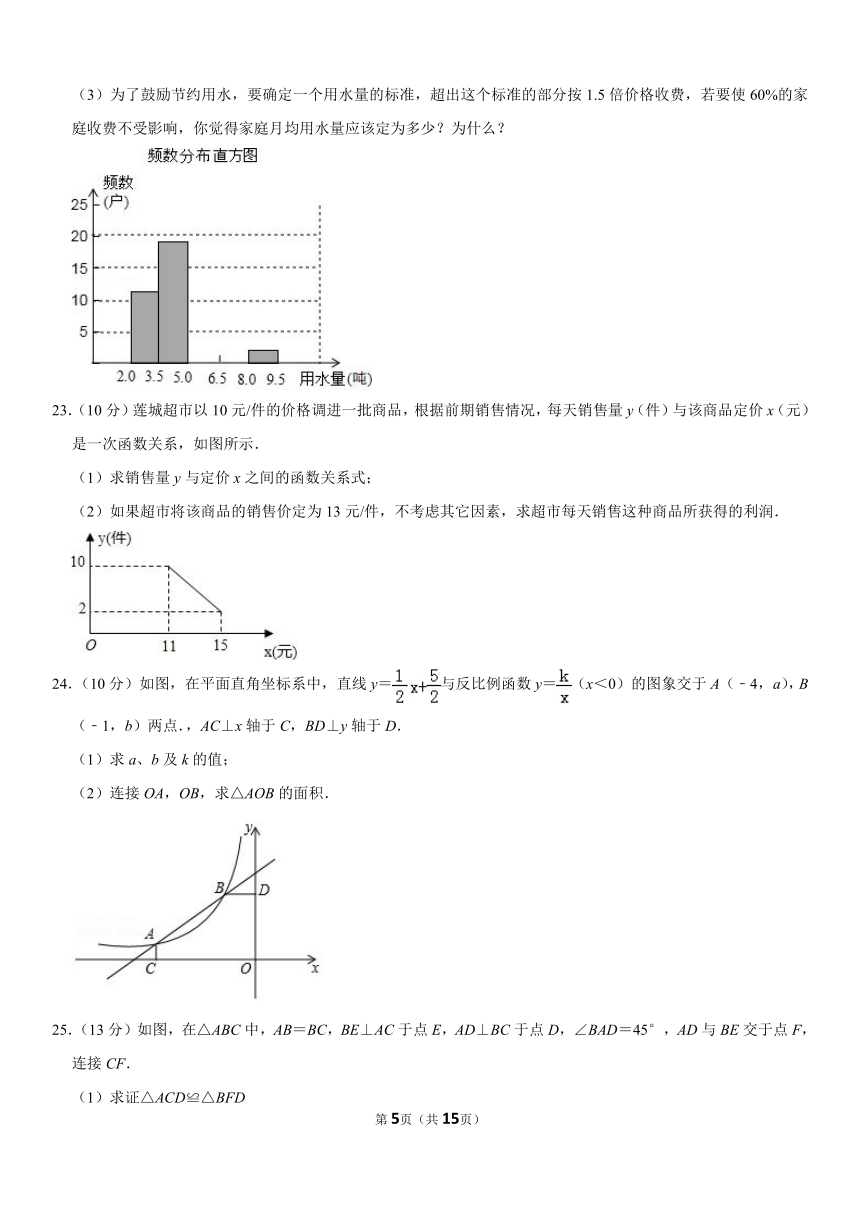
C.对角线相等
D.对角线互相垂直平分且相等
4.(4分)以下四组数中的三个数作为边长,不能构成直角三角形的是( )
A.1, , B.5,12,13 C.32,42,52 D.8,15,17.
5.(4分)已知? ABCD的周长为 32,AB=4,则 BC=( )
A.4 B.12 C.24 D.28
6.(4分)已知反比例函数 图象经过点(2,﹣3),则下列点中必在此函数图象上的是( )
A.(2,3) B.(1,6) C.(﹣1,6) D.(﹣2,﹣3)
7.(4分)已知正比例函数 y=kx(k≠0)的函数值 y随 x的增大而增大,则一次函数 y=kx+k的图象大致是( )
第 2页(共 15页)
A. B.
C. D.
8.(4分)点 P(﹣2,3)到 x轴的距离为( )
A.﹣2 B.1 C.2 D.3
9.(4分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了 40名学生,将结果绘制成了如图所示的
条形统计图,则参加绘画兴趣小组的频率是( )
A.0.1 B.0.15 C.0.25 D.0.3
10.(4分)点 A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数 y= 的图象上,若 x1<x2<0<x3,则 y1,y2,
y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
二、填空题(共 8小题,每小题 4分共 32分)
11.(4分)若一个直角三角形的两直角边长分别是 1、2,则第三边长为 .
12.(4分)若一个多边形的内角和是外角和的 5倍,则这个多边形是 边形.
13.(4分)如图,在 Rt△ABC中,∠ACB=90°,D是 AB的中点,CD=5cm,则 AB= cm.
14.(4分)已知菱形的两对角线长分别为 6cm和 8cm,则菱形的面积为 cm2.
15.(4分)在平面直角坐标系中,点 P(a﹣1,a)是第二象限内的点,则 a的取值范围是 .
16.(4分)已知△ABC中,D、E分别是 AB、AC边上的中点,且 DE=3cm,则 BC= cm.
第 3页(共 15页)
17.(4分)已知,如图,AB=AD=5,∠B=15°,CD⊥AB于 C,则 CD= .
18.(4分)如图,矩形 ABCD中,AB=8,BC=6.点 E在边 AB上,点 F在边 CD上,点 G、H在对角线 AC上,
若四边形 EGFH是菱形,则 AE的长是 .
三、解答题(共 8道,19题 6分,20-21题每题 8分,22-24题每题 10分,25-26题每题 13分)
19.(6分)如图,在平面直角坐标系 xOy中,A(﹣3,4),B(﹣4,1),C(﹣1,1).
(1)在图中作出△ABC关于 x轴的轴对称图形△A′B′C′;
(2)直接写出 A,B关于 y轴的对称点 A″,B″的坐标.
20.(8分)如图,在四边形 ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点 E,AF⊥CD交 CD的延长线于点
F.
求证:△ABE≌△ADF.
第 4页(共 15页)
21.(8分)如图,在? ABCD中,AC交 BD于点 O,点 E,点 F分别是 OA,OC的中点.
求证:四边形 BEDF为平行四边形.
22.(10分)某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的
50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0 19
5.0<x≤6.5
6.5<x≤8.0
8.0<x≤9.5
合计
2
50
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
第 5页(共 15页)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按 1.5倍价格收费,若要使 60%的家
庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
23.(10分)莲城超市以 10元/件的价格调进一批商品,根据前期销售情况,每天销售量 y(件)与该商品定价 x(元)
是一次函数关系,如图所示.
(1)求销售量 y与定价 x之间的函数关系式;
(2)如果超市将该商品的销售价定为 13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
24.(10分)如图,在平面直角坐标系中,直线 y= 与反比例函数 y= (x<0)的图象交于 A(﹣4,a),B
(﹣1,b)两点.,AC⊥x轴于 C,BD⊥y轴于 D.
(1)求 a、b及 k的值;
(2)连接 OA,OB,求△AOB的面积.
25.(13分)如图,在△ABC中,AB=BC,BE⊥AC于点 E,AD⊥BC于点 D,∠BAD=45°,AD与 BE交于点 F,
连接 CF.
(1)求证△ACD≌△BFD
第 6页(共 15页)
(2)求证:BF=2AE;
(3)若 CD= ,求 AD的长.
26.(13分)已知矩形 ABCD的一条边 AD=8,E是 BC边上的一点,将矩形 ABCD沿折痕 AE折叠,使得顶点 B
落在 CD边上的点 P处,PC=4(如图 1).
(1)求 AB的长;
(2)擦去折痕 AE,连结 PB,设 M是线段 PA的一个动点(点 M与点 P、A不重合).N是 AB沿长线上的一个
动点,并且满足 PM=BN.过点 M作 MH⊥PB,垂足为 H,连结 MN交 PB于点 F(如图 2).
①若 M是 PA的中点,求 MH的长;
②试问当点 M、N在移动过程中,线段 FH的长度是否发生变化?若变化,说明理由;若不变,求出线段 FH的
长度.
第 7页(共 15页)
2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共 10小题,每小题 4分共 40分)
1.【解答】解:四张交通标志图案的卡片中,只有第三张为中心对称图形.
故选:C.
2.【解答】解:A、利用了四边形的不稳定性,故错误;
B、利用了四边形的不稳定性,故错误;
C、利用了三角形的稳定性,正确;
D、四边形不具有稳定性,故错误,
故选:C.
3.【解答】解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选:A.
4.【解答】解:A、12+( )2=( )2,能构成直角三角形,故不符合题意;
B、52+122=132,能构成直角三角形,故不符合题意;
C、(32)2+(42)2≠(52)2,不能构成直角三角形,故符合题意;
D、82+152=172,能构成直角三角形,故不符合题意.
故选:C.
5.【解答】解:∵四边形 ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形 ABCD的周长是 32,
∴2(AB+BC)=32,
∴BC=12.
故选:B.
6.【解答】解:∵反比例函数 图象经过点(2,﹣3),
∴k=﹣6,
第 8页(共 15页)
∴y= ,
故选:C.
7.【解答】解:∵正比例函数 y=kx的函数值 y随 x的增大而增大,
∴k>0,
∵b=k>0,
∴一次函数 y=kx+k的图象经过一、二、三象限.
故选:A.
8.【解答】解:∵点 P的纵坐标为 3,
∴P点到 x轴的距离是 3.
故选:D.
9.【解答】解:∵根据条形统计图知道绘画兴趣小组的频数为 12,
∴参加绘画兴趣小组的频率是 12÷40=0.3.
故选:D.
10.【解答】解:∵反比例函数 y= 中,k=1>0,
∴此函数图象的两个分支在一、三象限,
∵x1<x2<0<x3,
∴A、B在第三象限,点 C在第一象限,
∴y1<0,y2<0,y3>0,
∵在第三象限 y随 x的增大而减小,
∴y1>y2,
∴y2<y1<y3.
故选:D.
二、填空题(共 8小题,每小题 4分共 32分)
11.【解答】解:∵直角三角形的两直角边长分别是 1和 2,
∴斜边= = ,
故答案为 .
12.【解答】解:多边形的外角和是 360°,根据题意得:180°?(n﹣2)=360°×5,
解得 n=12.
故答案为:十二.
第 9页(共 15页)
13.【解答】解:∵在 Rt△ABC中,∠ACB=90°,D是 AB的中点,
∴线段 CD是斜边 AB上的中线;
又∵CD=5cm,
∴AB=2CD=10cm.
故答案是:10.
14.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半
即:6×8÷2=24cm2.
故答案为:24.
15.【解答】解:∵点 P(a﹣1,a)是第二象限内的点,
∴a﹣1<0且 a>0,解得:0<a<1.故答案填:0<a<1.
16.【解答】解:∵△ABC中,D、E分别是 AB、AC边上的中点,
∴DE是三角形的中位线,
∵DE=3cm,
∴BC=2DE=6cm.
故答案为:6.
17.【解答】解:∵AB=AD,
∴∠ADB=∠B=15°,
∴∠DAC=∠ADB+∠B=30°,
又∵CD⊥AB,
∴CD= AD= ×5=2.5.
故答案为:2.5.
18.【解答】解:连接 FE,交 AC于点 O.
∵四边形 ABCD是矩形,
∴∠FCH=∠EAG.
∵四边形 EGFH是菱形,
∴FH=GE,∠FHG=∠EGH.
∴∠FHC=∠EGA.
∴△FCH≌△EAG(AAS).
∴CH=AG.
∵四边形 EGFH是菱形,
第 10页(共 15页)
∴FE⊥GH,且 O为 GH中点.
∴O为 AC中点.
在 Rt△ABC中,利用勾股定理可得 AC=10.
∴AO=5.
则 cos∠OAE=cos∠CAB,
∴ ,即 ,解得 AE= .
故答案为 .
三、解答题(共 8道,19题 6分,20-21题每题 8分,22-24题每题 10分,25-26题每题 13分)
19.【解答】解:(1)如图所示,△A′B′C′即为所求;
(2)∵A(﹣3,4),B(﹣4,1),
∴A″(3,4),B″(4,1).
20.【解答】证明:∵CA平分∠BCD,AE⊥BC于点 E,AF⊥CD交 CD的延长线于点 F,
∴AE=AF.
在 Rt△ABE与 Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL).
21.【解答】证明:∵四边形 ABCD是平行四边形,
第 11页(共 15页)
∴AO=CO,BO=DO,
又∵点 E,点 F分别是 OA,OC的中点,
∴EO= ,FO= ,
∴EO=FO,
∴四边形 BEDF为平行四边形.
22.【解答】解:(1)频数分布表如下:
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0 19
5.0<x≤6.5
6.5<x≤8.0
13
5
8.0<x≤9.5
合计
2
50
频数分布直方图如下:
(2)从直方图可以看出:①居民月平均用水量大部分在 2.0至 6.5之间;②居民月平均用水量在 3.5<x≤5.0范
围内的最多,有 19户;
(3)要使 60%的家庭收费不受影响,你觉得家庭月均用水量应该定为 5吨,因为月平均用水量不超过 5吨的有
第 12页(共 15页)
30户,30÷50=60%.
23.【解答】解:(1)设 y=kx+b(k≠0),由图象可知,
,
解得 ,
故销售量 y与定价 x之间的函数关系式是:y=﹣2x+32;
(2)超市每天销售这种商品所获得的利润是:
W=(﹣2x+32)(13﹣10)=﹣6x+96,
当 x=13(元)时,超市每天销售这种商品所获得的利润是:
W=﹣6×13+96=18(元).
24.【解答】解:(1)将点 A(﹣4,a)、B(﹣1,b)分别代入表达式 中,得: ;
,
∴ ,
将 B(﹣1,2)代入 y= 中,得 k=﹣2,
所以 a= ,b=2,k=﹣2;
(2)设直线 AB分别交 x轴、y轴于点 E,F
对于直线 ,分别令 y=0,x=0,解得:x=﹣5,y= ,
∴E(﹣5,0),F( ),
∵S△AEO= ×OE×AC= ,S△BFO= ×OF×BD= ,S△EOF= ×OE×OF=
,
∴S△AOB=S△EOF﹣S△AEO﹣S△BFO= .
第 13页(共 15页)
25.【解答】(1)∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中, ,
∴△ACD≌△BFD(ASA);
(2)证明:由(1)可知:BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(3)解:∵△ACD≌△BFD,
∴DF=CD= ,
在 Rt△CDF中,CF= =2,
∵BE⊥AC,AE=EC,
∴AF=CF=2.
∴AD=AF+DF=2+ .
26.【解答】解:(1)设 AB=x,则 AP=CD=x,DP=CD﹣CP=x﹣4,
在 Rt△ADP中,AD2+DP2=AP2,
即 82+(x﹣4)2=x2,
解得:x=10,
即 AB=10.
(2)①如图 2,过点 A作 AG⊥PB于点 G,
第 14页(共 15页)
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB= ,
∵AP=AB,
∴PG=BG= PB=2 ,
在 Rt△AGP中,AG= ,
∵AG⊥PB,MH⊥PB,
∴MH∥AG,
∵M是 PA的中点,
∴H是 PG的中点,
∴MH= AG= .
②当点 M、N在移动过程中,线段 FH的长度是不发生变化;
作 MQ∥AN,交 PB于点 Q,如图 3,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
第 15页(共 15页)
∵MP=MQ,MH⊥PQ,
∴HQ= PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
,
∴△MFQ≌△NFB(AAS).
∴QF= QB,
∴HF=HQ+QF= PQ+ QB= PB= .
∴当点 M、N在移动过程中,线段 FH的长度是不发生变化,长度为 2 .
2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷
一.选择题(共 10小题,每小题 4分共 40分)
1.(4分)下列交通标志图案中,是中心对称图形的是( )
A. B. C. D.
2.(4分)在实际生活中,我们经常利用一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )
A. 电动伸缩门 B. 升降台
C. 栅栏 D. 窗户
3.(4分)平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直平分且相等
4.(4分)以下四组数中的三个数作为边长,不能构成直角三角形的是( )
A.1, , B.5,12,13 C.32,42,52 D.8,15,17.
5.(4分)已知? ABCD的周长为 32,AB=4,则 BC=( )
A.4 B.12 C.24 D.28
6.(4分)已知反比例函数 图象经过点(2,﹣3),则下列点中必在此函数图象上的是( )
A.(2,3) B.(1,6) C.(﹣1,6) D.(﹣2,﹣3)
7.(4分)已知正比例函数 y=kx(k≠0)的函数值 y随 x的增大而增大,则一次函数 y=kx+k的图象大致是( )
第 2页(共 15页)
A. B.
C. D.
8.(4分)点 P(﹣2,3)到 x轴的距离为( )
A.﹣2 B.1 C.2 D.3
9.(4分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了 40名学生,将结果绘制成了如图所示的
条形统计图,则参加绘画兴趣小组的频率是( )
A.0.1 B.0.15 C.0.25 D.0.3
10.(4分)点 A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数 y= 的图象上,若 x1<x2<0<x3,则 y1,y2,
y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
二、填空题(共 8小题,每小题 4分共 32分)
11.(4分)若一个直角三角形的两直角边长分别是 1、2,则第三边长为 .
12.(4分)若一个多边形的内角和是外角和的 5倍,则这个多边形是 边形.
13.(4分)如图,在 Rt△ABC中,∠ACB=90°,D是 AB的中点,CD=5cm,则 AB= cm.
14.(4分)已知菱形的两对角线长分别为 6cm和 8cm,则菱形的面积为 cm2.
15.(4分)在平面直角坐标系中,点 P(a﹣1,a)是第二象限内的点,则 a的取值范围是 .
16.(4分)已知△ABC中,D、E分别是 AB、AC边上的中点,且 DE=3cm,则 BC= cm.
第 3页(共 15页)
17.(4分)已知,如图,AB=AD=5,∠B=15°,CD⊥AB于 C,则 CD= .
18.(4分)如图,矩形 ABCD中,AB=8,BC=6.点 E在边 AB上,点 F在边 CD上,点 G、H在对角线 AC上,
若四边形 EGFH是菱形,则 AE的长是 .
三、解答题(共 8道,19题 6分,20-21题每题 8分,22-24题每题 10分,25-26题每题 13分)
19.(6分)如图,在平面直角坐标系 xOy中,A(﹣3,4),B(﹣4,1),C(﹣1,1).
(1)在图中作出△ABC关于 x轴的轴对称图形△A′B′C′;
(2)直接写出 A,B关于 y轴的对称点 A″,B″的坐标.
20.(8分)如图,在四边形 ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点 E,AF⊥CD交 CD的延长线于点
F.
求证:△ABE≌△ADF.
第 4页(共 15页)
21.(8分)如图,在? ABCD中,AC交 BD于点 O,点 E,点 F分别是 OA,OC的中点.
求证:四边形 BEDF为平行四边形.
22.(10分)某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的
50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0 19
5.0<x≤6.5
6.5<x≤8.0
8.0<x≤9.5
合计
2
50
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
第 5页(共 15页)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按 1.5倍价格收费,若要使 60%的家
庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
23.(10分)莲城超市以 10元/件的价格调进一批商品,根据前期销售情况,每天销售量 y(件)与该商品定价 x(元)
是一次函数关系,如图所示.
(1)求销售量 y与定价 x之间的函数关系式;
(2)如果超市将该商品的销售价定为 13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
24.(10分)如图,在平面直角坐标系中,直线 y= 与反比例函数 y= (x<0)的图象交于 A(﹣4,a),B
(﹣1,b)两点.,AC⊥x轴于 C,BD⊥y轴于 D.
(1)求 a、b及 k的值;
(2)连接 OA,OB,求△AOB的面积.
25.(13分)如图,在△ABC中,AB=BC,BE⊥AC于点 E,AD⊥BC于点 D,∠BAD=45°,AD与 BE交于点 F,
连接 CF.
(1)求证△ACD≌△BFD
第 6页(共 15页)
(2)求证:BF=2AE;
(3)若 CD= ,求 AD的长.
26.(13分)已知矩形 ABCD的一条边 AD=8,E是 BC边上的一点,将矩形 ABCD沿折痕 AE折叠,使得顶点 B
落在 CD边上的点 P处,PC=4(如图 1).
(1)求 AB的长;
(2)擦去折痕 AE,连结 PB,设 M是线段 PA的一个动点(点 M与点 P、A不重合).N是 AB沿长线上的一个
动点,并且满足 PM=BN.过点 M作 MH⊥PB,垂足为 H,连结 MN交 PB于点 F(如图 2).
①若 M是 PA的中点,求 MH的长;
②试问当点 M、N在移动过程中,线段 FH的长度是否发生变化?若变化,说明理由;若不变,求出线段 FH的
长度.
第 7页(共 15页)
2018-2019学年湖南省株洲市醴陵市八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共 10小题,每小题 4分共 40分)
1.【解答】解:四张交通标志图案的卡片中,只有第三张为中心对称图形.
故选:C.
2.【解答】解:A、利用了四边形的不稳定性,故错误;
B、利用了四边形的不稳定性,故错误;
C、利用了三角形的稳定性,正确;
D、四边形不具有稳定性,故错误,
故选:C.
3.【解答】解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选:A.
4.【解答】解:A、12+( )2=( )2,能构成直角三角形,故不符合题意;
B、52+122=132,能构成直角三角形,故不符合题意;
C、(32)2+(42)2≠(52)2,不能构成直角三角形,故符合题意;
D、82+152=172,能构成直角三角形,故不符合题意.
故选:C.
5.【解答】解:∵四边形 ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形 ABCD的周长是 32,
∴2(AB+BC)=32,
∴BC=12.
故选:B.
6.【解答】解:∵反比例函数 图象经过点(2,﹣3),
∴k=﹣6,
第 8页(共 15页)
∴y= ,
故选:C.
7.【解答】解:∵正比例函数 y=kx的函数值 y随 x的增大而增大,
∴k>0,
∵b=k>0,
∴一次函数 y=kx+k的图象经过一、二、三象限.
故选:A.
8.【解答】解:∵点 P的纵坐标为 3,
∴P点到 x轴的距离是 3.
故选:D.
9.【解答】解:∵根据条形统计图知道绘画兴趣小组的频数为 12,
∴参加绘画兴趣小组的频率是 12÷40=0.3.
故选:D.
10.【解答】解:∵反比例函数 y= 中,k=1>0,
∴此函数图象的两个分支在一、三象限,
∵x1<x2<0<x3,
∴A、B在第三象限,点 C在第一象限,
∴y1<0,y2<0,y3>0,
∵在第三象限 y随 x的增大而减小,
∴y1>y2,
∴y2<y1<y3.
故选:D.
二、填空题(共 8小题,每小题 4分共 32分)
11.【解答】解:∵直角三角形的两直角边长分别是 1和 2,
∴斜边= = ,
故答案为 .
12.【解答】解:多边形的外角和是 360°,根据题意得:180°?(n﹣2)=360°×5,
解得 n=12.
故答案为:十二.
第 9页(共 15页)
13.【解答】解:∵在 Rt△ABC中,∠ACB=90°,D是 AB的中点,
∴线段 CD是斜边 AB上的中线;
又∵CD=5cm,
∴AB=2CD=10cm.
故答案是:10.
14.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半
即:6×8÷2=24cm2.
故答案为:24.
15.【解答】解:∵点 P(a﹣1,a)是第二象限内的点,
∴a﹣1<0且 a>0,解得:0<a<1.故答案填:0<a<1.
16.【解答】解:∵△ABC中,D、E分别是 AB、AC边上的中点,
∴DE是三角形的中位线,
∵DE=3cm,
∴BC=2DE=6cm.
故答案为:6.
17.【解答】解:∵AB=AD,
∴∠ADB=∠B=15°,
∴∠DAC=∠ADB+∠B=30°,
又∵CD⊥AB,
∴CD= AD= ×5=2.5.
故答案为:2.5.
18.【解答】解:连接 FE,交 AC于点 O.
∵四边形 ABCD是矩形,
∴∠FCH=∠EAG.
∵四边形 EGFH是菱形,
∴FH=GE,∠FHG=∠EGH.
∴∠FHC=∠EGA.
∴△FCH≌△EAG(AAS).
∴CH=AG.
∵四边形 EGFH是菱形,
第 10页(共 15页)
∴FE⊥GH,且 O为 GH中点.
∴O为 AC中点.
在 Rt△ABC中,利用勾股定理可得 AC=10.
∴AO=5.
则 cos∠OAE=cos∠CAB,
∴ ,即 ,解得 AE= .
故答案为 .
三、解答题(共 8道,19题 6分,20-21题每题 8分,22-24题每题 10分,25-26题每题 13分)
19.【解答】解:(1)如图所示,△A′B′C′即为所求;
(2)∵A(﹣3,4),B(﹣4,1),
∴A″(3,4),B″(4,1).
20.【解答】证明:∵CA平分∠BCD,AE⊥BC于点 E,AF⊥CD交 CD的延长线于点 F,
∴AE=AF.
在 Rt△ABE与 Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL).
21.【解答】证明:∵四边形 ABCD是平行四边形,
第 11页(共 15页)
∴AO=CO,BO=DO,
又∵点 E,点 F分别是 OA,OC的中点,
∴EO= ,FO= ,
∴EO=FO,
∴四边形 BEDF为平行四边形.
22.【解答】解:(1)频数分布表如下:
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0 19
5.0<x≤6.5
6.5<x≤8.0
13
5
8.0<x≤9.5
合计
2
50
频数分布直方图如下:
(2)从直方图可以看出:①居民月平均用水量大部分在 2.0至 6.5之间;②居民月平均用水量在 3.5<x≤5.0范
围内的最多,有 19户;
(3)要使 60%的家庭收费不受影响,你觉得家庭月均用水量应该定为 5吨,因为月平均用水量不超过 5吨的有
第 12页(共 15页)
30户,30÷50=60%.
23.【解答】解:(1)设 y=kx+b(k≠0),由图象可知,
,
解得 ,
故销售量 y与定价 x之间的函数关系式是:y=﹣2x+32;
(2)超市每天销售这种商品所获得的利润是:
W=(﹣2x+32)(13﹣10)=﹣6x+96,
当 x=13(元)时,超市每天销售这种商品所获得的利润是:
W=﹣6×13+96=18(元).
24.【解答】解:(1)将点 A(﹣4,a)、B(﹣1,b)分别代入表达式 中,得: ;
,
∴ ,
将 B(﹣1,2)代入 y= 中,得 k=﹣2,
所以 a= ,b=2,k=﹣2;
(2)设直线 AB分别交 x轴、y轴于点 E,F
对于直线 ,分别令 y=0,x=0,解得:x=﹣5,y= ,
∴E(﹣5,0),F( ),
∵S△AEO= ×OE×AC= ,S△BFO= ×OF×BD= ,S△EOF= ×OE×OF=
,
∴S△AOB=S△EOF﹣S△AEO﹣S△BFO= .
第 13页(共 15页)
25.【解答】(1)∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中, ,
∴△ACD≌△BFD(ASA);
(2)证明:由(1)可知:BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(3)解:∵△ACD≌△BFD,
∴DF=CD= ,
在 Rt△CDF中,CF= =2,
∵BE⊥AC,AE=EC,
∴AF=CF=2.
∴AD=AF+DF=2+ .
26.【解答】解:(1)设 AB=x,则 AP=CD=x,DP=CD﹣CP=x﹣4,
在 Rt△ADP中,AD2+DP2=AP2,
即 82+(x﹣4)2=x2,
解得:x=10,
即 AB=10.
(2)①如图 2,过点 A作 AG⊥PB于点 G,
第 14页(共 15页)
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB= ,
∵AP=AB,
∴PG=BG= PB=2 ,
在 Rt△AGP中,AG= ,
∵AG⊥PB,MH⊥PB,
∴MH∥AG,
∵M是 PA的中点,
∴H是 PG的中点,
∴MH= AG= .
②当点 M、N在移动过程中,线段 FH的长度是不发生变化;
作 MQ∥AN,交 PB于点 Q,如图 3,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
第 15页(共 15页)
∵MP=MQ,MH⊥PQ,
∴HQ= PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
,
∴△MFQ≌△NFB(AAS).
∴QF= QB,
∴HF=HQ+QF= PQ+ QB= PB= .
∴当点 M、N在移动过程中,线段 FH的长度是不发生变化,长度为 2 .
同课章节目录
