12.3 一次函数与二元一次方程学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 12.3 一次函数与二元一次方程学案(要点讲解+当堂检测+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 11:42:44 | ||
图片预览


文档简介
沪科版数学八年级上册同步学案
第12章 一次函数
12.3 一次函数与二元一次方程
要 点 讲 解
要点一 一次函数与二元一次方程的关系
1. 任意—个一次函数y=kx+b(k≠0)都可以化成以自变量x和函数y为未知数的二元一次方程kx-y=-b(k≠0)的形式,于是有下面结论:
(1)一次函数y=kx+b(k≠0)的图象上任意一点的坐标都是二元一次方程kx-y=-b(k≠0)的一组解.
(2)以二元一次方程是kx-y=-b(k≠0)的解为坐标的点都在一次函数y=kx+b(k≠0)的图象上.
(3)对于同一个数学模型y=kx+b(k≠0),若将其中的x,y看作变量,则它表示一个一次函数;若将x,y看作未知数,则它就是一个二元一次方程.
2. 一般地,任何一个二元一次方程都可以转化成一次函数的形式,所以每个二元一次方程的图象都是一条直线,这样,解二元一次方程组就转化为在平面直角坐标系里研究两条直线的交点问题.
经典例题1 一次函数y1=x+4的图象如图所示,则一次函数y2=-x+b的图象与y1=x+4的图象的交点不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:由图可知,一次函数y1=x+4的图象经过第一、二、三象限,根据交点坐标一定在函数图象上,得两函数的图象的交点不可能在第四象限.
答案:D
要点二 二元一次方程组的图象解法
如何利用图象解二元一次方程组:
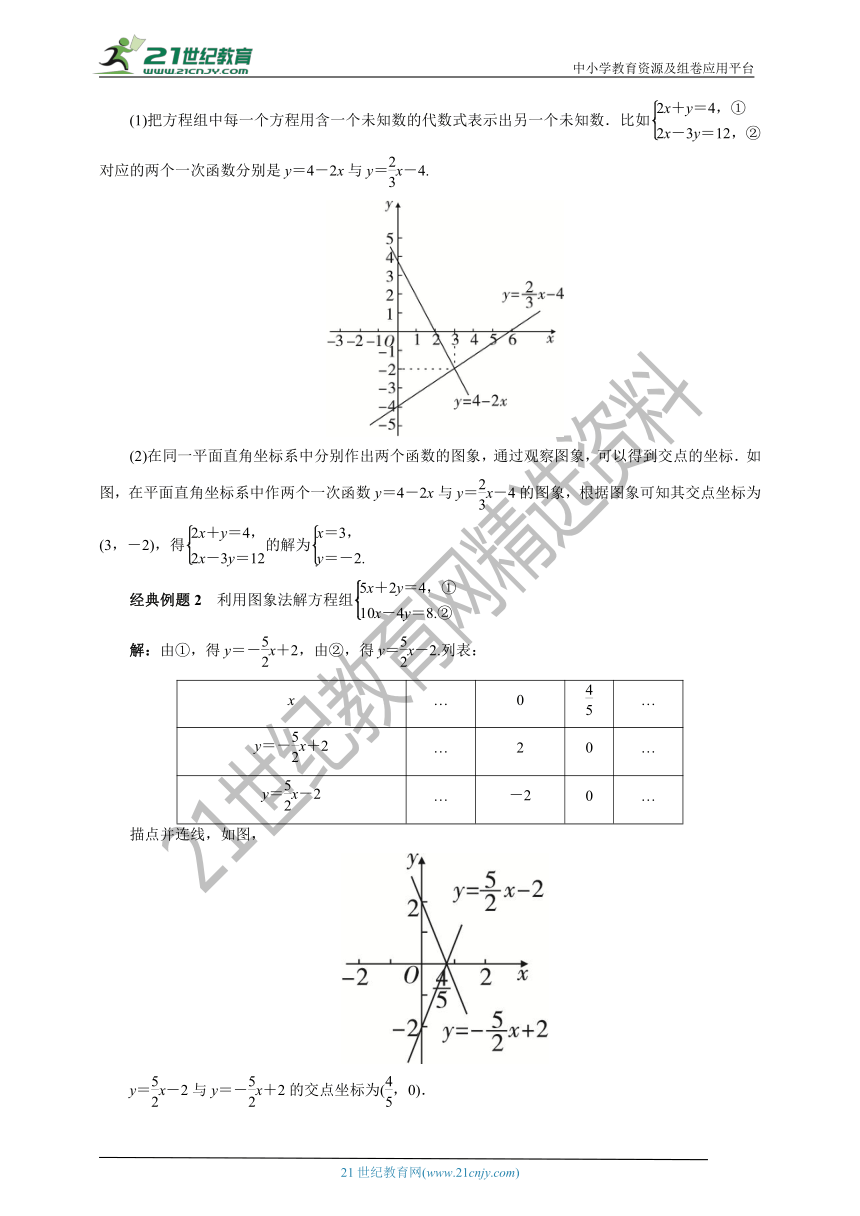
(1)把方程组中每一个方程用含一个未知数的代数式表示出另一个未知数.比如对应的两个一次函数分别是y=4-2x与y=x-4.
(2)在同一平面直角坐标系中分别作出两个函数的图象,通过观察图象,可以得到交点的坐标.如图,在平面直角坐标系中作两个一次函数y=4-2x与y=x-4的图象,根据图象可知其交点坐标为(3,-2),得的解为
经典例题2 利用图象法解方程组
解:由①,得y=-x+2,由②,得y=x-2.列表:
x
…
0
…
y=-x+2
…
2
0
…
y=x-2
…
-2
0
…
描点并连线,如图,
y=x-2与y=-x+2的交点坐标为(,0).
所以方程组的解为
要点三 二元一次方程组解的情况与系数比的关系
1. 关于x,y的二元一次方程组(a1,a2,b1,b2都是不为0的常数,c1,c2为常数),直线l1是方程a1x+b1y=c1对应的直线,直线l2是方程a2x+b2y=c2对应的直线.
2. 当l1与l2相交时,两个图象只有唯一的交点,方程组有唯一的解,此时≠.
3. 当l1与l2重合为一条直线时,图象上任意一点的坐标都同时适合两个方程,方程组有无数组解,此时==(c2≠0).
4. 当l1∥l2时,两个图象没有交点,这时方程组无解,此时=≠(c2≠0).
5. 将二元一次方程组的两个方程分别化成一次函数的形式为l1:y=k1x+b1和l2:y=k2x+b2.(1)当k1≠k2时,两图象有唯一交点,方程组有唯一的解;(2)当k1=k2,且b1=b2时,两图象重合,方程组有无数组解;(3)当k1=k2且b1≠b2时,两条直线平行,方程组无解.
经典例题3 既不解方程也不画图,你能判断下列方程组解的情况吗?
(1)(2)
解析:不解方程也不画图,判断方程组解的情况,首先需要将方程组中的两个二元一次方程化为ax+by=c的形式,然后根据相应系数及常数项的比值情况确定两个二元一次方程所对应的直线的位置关系,从而可以判断方程组解的情况.
解:(1)原方程组可化为
因为≠,所以此方程组有唯一一组解.
(2)原方程组可化为
因为=≠,所以此方程组无解.
当 堂 检 测
1. 下列有序数对是二元一次方程3x+2y=7的解的是( )
A. (-1,4) B. (1,-2) C. (2,) D. (,2)
2. 点P为直线3x+y=10上的任意点,满足横、纵坐标均为正整数的P点有( )
A. 1个 B. 3个 C. 4个 D. 无数个
3. 两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A. (-2,3) B. (2,-3) C. (-2,-3) D. (2,3)
4. 用图象法解方程组时,下列选项中正确的是( )
A B C D
5. 若二元一次方程组有无数组解,那么k应满足的条件是( )
A. k=- B. k=
C. k为任意有理数 D. 以上都不对
6. 点(-2,5) (填“在”或“不在”)一次函数y=-3x+1的图象上; (填“是”或“不是”)方程2x+y=1的解.
7. 已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组的解是 .
8. 利用图象法解方程组
9. 在同一平面直角坐标系内画出一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y10且y2<0?
当堂检测参考答案
1. C 2. B 3. D 4. C 5. A
6. 不在 是
7.
8. 解:由 得如图所示,在同一直角坐标系中分别画出它们的图象,它们的交点坐标是(2,-1),所以二元一次方程组的解是
9. 解:如图所示.
(1)因为一次函数y1=-x+4和y2=2x-5的图象相交于点(3,1).所以方程-x+4=2x-5的解为x=3.
(2)由图可知当x>3时,y10且y2<0.
第12章 一次函数
12.3 一次函数与二元一次方程
要 点 讲 解
要点一 一次函数与二元一次方程的关系
1. 任意—个一次函数y=kx+b(k≠0)都可以化成以自变量x和函数y为未知数的二元一次方程kx-y=-b(k≠0)的形式,于是有下面结论:
(1)一次函数y=kx+b(k≠0)的图象上任意一点的坐标都是二元一次方程kx-y=-b(k≠0)的一组解.
(2)以二元一次方程是kx-y=-b(k≠0)的解为坐标的点都在一次函数y=kx+b(k≠0)的图象上.
(3)对于同一个数学模型y=kx+b(k≠0),若将其中的x,y看作变量,则它表示一个一次函数;若将x,y看作未知数,则它就是一个二元一次方程.
2. 一般地,任何一个二元一次方程都可以转化成一次函数的形式,所以每个二元一次方程的图象都是一条直线,这样,解二元一次方程组就转化为在平面直角坐标系里研究两条直线的交点问题.
经典例题1 一次函数y1=x+4的图象如图所示,则一次函数y2=-x+b的图象与y1=x+4的图象的交点不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:由图可知,一次函数y1=x+4的图象经过第一、二、三象限,根据交点坐标一定在函数图象上,得两函数的图象的交点不可能在第四象限.
答案:D
要点二 二元一次方程组的图象解法
如何利用图象解二元一次方程组:
(1)把方程组中每一个方程用含一个未知数的代数式表示出另一个未知数.比如对应的两个一次函数分别是y=4-2x与y=x-4.
(2)在同一平面直角坐标系中分别作出两个函数的图象,通过观察图象,可以得到交点的坐标.如图,在平面直角坐标系中作两个一次函数y=4-2x与y=x-4的图象,根据图象可知其交点坐标为(3,-2),得的解为
经典例题2 利用图象法解方程组
解:由①,得y=-x+2,由②,得y=x-2.列表:
x
…
0
…
y=-x+2
…
2
0
…
y=x-2
…
-2
0
…
描点并连线,如图,
y=x-2与y=-x+2的交点坐标为(,0).
所以方程组的解为
要点三 二元一次方程组解的情况与系数比的关系
1. 关于x,y的二元一次方程组(a1,a2,b1,b2都是不为0的常数,c1,c2为常数),直线l1是方程a1x+b1y=c1对应的直线,直线l2是方程a2x+b2y=c2对应的直线.
2. 当l1与l2相交时,两个图象只有唯一的交点,方程组有唯一的解,此时≠.
3. 当l1与l2重合为一条直线时,图象上任意一点的坐标都同时适合两个方程,方程组有无数组解,此时==(c2≠0).
4. 当l1∥l2时,两个图象没有交点,这时方程组无解,此时=≠(c2≠0).
5. 将二元一次方程组的两个方程分别化成一次函数的形式为l1:y=k1x+b1和l2:y=k2x+b2.(1)当k1≠k2时,两图象有唯一交点,方程组有唯一的解;(2)当k1=k2,且b1=b2时,两图象重合,方程组有无数组解;(3)当k1=k2且b1≠b2时,两条直线平行,方程组无解.
经典例题3 既不解方程也不画图,你能判断下列方程组解的情况吗?
(1)(2)
解析:不解方程也不画图,判断方程组解的情况,首先需要将方程组中的两个二元一次方程化为ax+by=c的形式,然后根据相应系数及常数项的比值情况确定两个二元一次方程所对应的直线的位置关系,从而可以判断方程组解的情况.
解:(1)原方程组可化为
因为≠,所以此方程组有唯一一组解.
(2)原方程组可化为
因为=≠,所以此方程组无解.
当 堂 检 测
1. 下列有序数对是二元一次方程3x+2y=7的解的是( )
A. (-1,4) B. (1,-2) C. (2,) D. (,2)
2. 点P为直线3x+y=10上的任意点,满足横、纵坐标均为正整数的P点有( )
A. 1个 B. 3个 C. 4个 D. 无数个
3. 两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A. (-2,3) B. (2,-3) C. (-2,-3) D. (2,3)
4. 用图象法解方程组时,下列选项中正确的是( )
A B C D
5. 若二元一次方程组有无数组解,那么k应满足的条件是( )
A. k=- B. k=
C. k为任意有理数 D. 以上都不对
6. 点(-2,5) (填“在”或“不在”)一次函数y=-3x+1的图象上; (填“是”或“不是”)方程2x+y=1的解.
7. 已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组的解是 .
8. 利用图象法解方程组
9. 在同一平面直角坐标系内画出一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y1
当堂检测参考答案
1. C 2. B 3. D 4. C 5. A
6. 不在 是
7.
8. 解:由 得如图所示,在同一直角坐标系中分别画出它们的图象,它们的交点坐标是(2,-1),所以二元一次方程组的解是
9. 解:如图所示.
(1)因为一次函数y1=-x+4和y2=2x-5的图象相交于点(3,1).所以方程-x+4=2x-5的解为x=3.
(2)由图可知当x>3时,y1
