12.4 综合与实践 一次函数模型的应用学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 12.4 综合与实践 一次函数模型的应用学案(要点讲解+当堂检测+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 11:46:29 | ||
图片预览


文档简介
沪科版数学八年级上册同步学案
第12章 一次函数
12.4 综合与实践 一次函数模型的应用
要 点 讲 解
要点 一次函数模型的应用
建立两个变量之间的函数关系,从实际问题中抽象出一次函数的模型,可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在坐标平面内描出相应的点(若干个).
(2)观察描出的点在坐标平面内的分布情况,从而推测函数图象的大致形状,并据此进一步猜想x与y之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验,必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
经典例题 某商店销售某种新型化工原料,其市场指导价是每千克160元(该商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.
(1)为了扩大销售量,该商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润.那么该商店调整价格后的标价是多少元?打折后的实际售价是多少元?
(2)该商店为了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:
实际售价x(元/千克)
…
150
160
170
180
…
月销售量y(千克)
…
500
480
460
440
…
①请你在所给的平面直角坐标系(如图)中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;
②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;
③若该商店某月按同一实际售价共卖出这种原料450千克,请你求出该商店这个月销售这种原料的利润是多少元.
解:(1)依题意知,每千克原料的进货价为160×75%=120(元).
设该商店调整价格后的标价为x元,则0.8x-120=0.8x×20%,解得x=187.5,187.5×0.8=150(元),所以调整价格后的标价是187.5元,打折后的实际售价是150元.
(2)①描点、画图,如图所示,观察图象,可知这些点的发展趋势近似是一条直线,所以猜想y与x之间存在着一次函数关系.
②根据①中的猜想,设y与x之间的函数表达式为y=kx+b(k≠0),将点(150,500)和(160,480)代入表达式,得解得
所以y与x之间的函数表达式为y=-2x+800.
将点(170,460)和(180,440)代入y=-2x+800,均成立,即这些点都符合y=-2x+800.所以y与x之间为一次函数关系.
所以①中猜想y与x之间存在着一次函数关系是正确的.
③设该商店这个月销售这种原料的利润为w元,
当y=450时,x=175,所以w=(175-120)×450=24750.答:该商店这个月销售这种原料的利润为24750元.
当 堂 检 测
1. 在某次实验中,测得两个变量m和v之间的4组对应数据如下表,则m和v之间的关系最接近于下列关系式中的( )
m
1
2
3
4
v
0.01
2.9
6.03
9.1
A. v=2m-2 B. v=2m-1
C. v=3m-3 D. v=m+1
2. 对于气温,有的地方用摄氏温度表示,有些地方用华氏温度表示,摄氏温度与华氏温度之间存在着某种函数关系,从温度计上可以看出摄氏温度x(℃)与华氏温度y()有如下表所示的对应关系,则确定y与x之间的函数关系是( )
x(℃)
…
-10
0
10
20
30
…
y()
…
14
32
50
68
86
…
A. y=x B. y=1.8x+32
C. y=0.56x2+7.4 x+32 D. y=2.1x+26
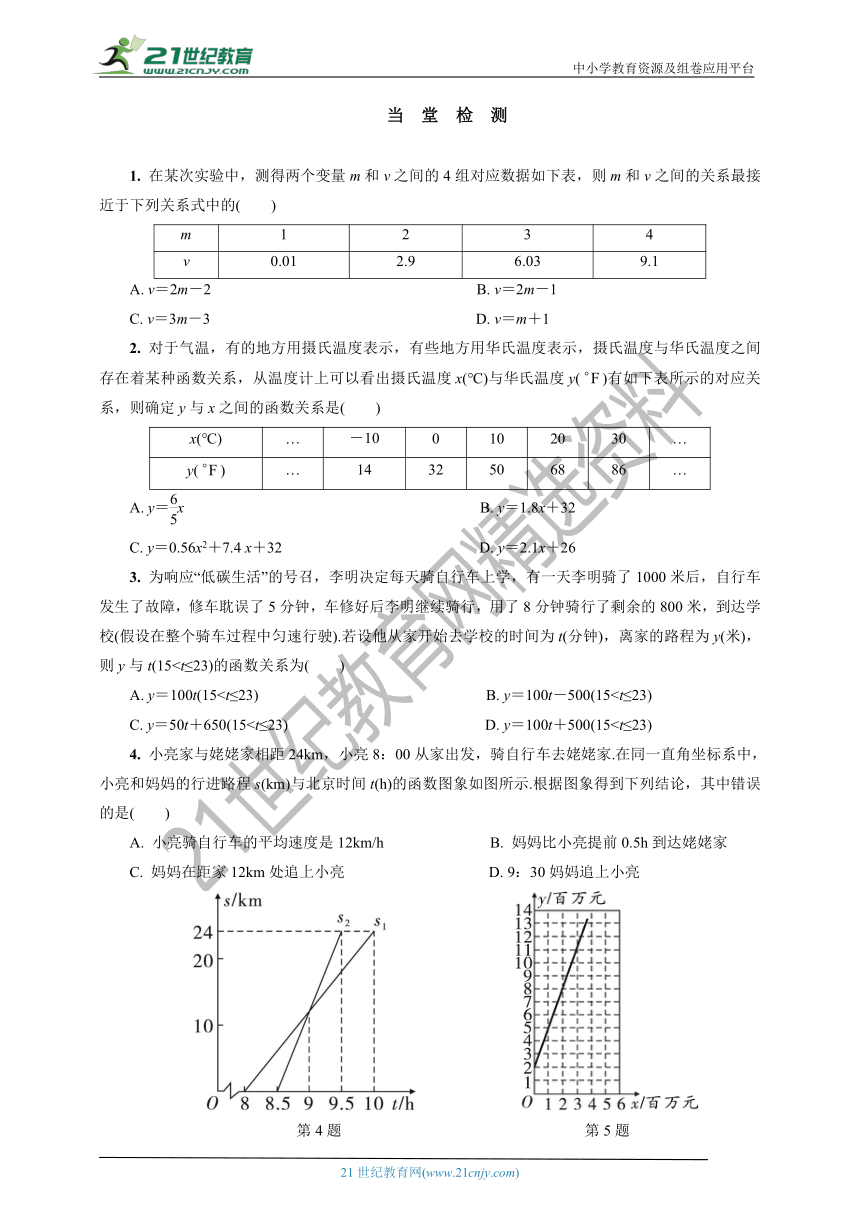
3. 为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在整个骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(米),则y与t(15A. y=100t(15C. y=50t+650(154. 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与北京时间t(h)的函数图象如图所示.根据图象得到下列结论,其中错误的是( )
A. 小亮骑自行车的平均速度是12km/h B. 妈妈比小亮提前0.5h到达姥姥家
C. 妈妈在距家12km处追上小亮 D. 9:30妈妈追上小亮
第4题 第5题
5. 某种产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间的函数关系图象如图所示.则y与x之间的函数表达式是 .
6. 某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如下表:
时间t(天)
1
3
6
10
16
…
日销售量m(件)
94
90
84
76
64
…
通过认真分析上表的数据,用所学过的函数知识:
(1)确定满足这些数据的m(件)与t(天)之间的函数表达式;
(2)判断它是否符合预测函数模型.
7. 健身运动已成为时尚,某公司计划组装A,B两种型号的健身器材共40套,捐赠给社区健身中心.组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A,B两种型号的健身器材时,共有多少种组装方案;
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元.求总组装费用最少的组装方案,最少组装费用是多少?
当堂检测参考答案
1. C 2. B 3. B 4. D
5. y=3x+2
6. 解:(1)设m(件)与t(天)的函数模型为m=kt+b,将(1,94),(3,90)代入可求得k=-2,b=96,所以m=-2t+96.
(2)经检验,其它点的坐标均符合以上表达式,所以符合预测函数模型.
7. 解:(1)设该公司组装A型器材x套,则组装B型器材(40-x)套,依题意,得解得22≤x≤30.因为x为整数,所以x可取22,23,24,25,26,27,28,29,30.所以组装A,B两种型号的健身器材共有9种组装方案.
(2)总组装费用y=20x+18(40-x)=2x+720.因为k=2>0,所以y随x的增大而增大.所以当x=22时,总组装费用最少,总组装费用最少是2×22+720=764(元).所以总组装费用最少的组装方案是:组装A型器材22套,组装B型器材18套,最少组装费用是764元.
第12章 一次函数
12.4 综合与实践 一次函数模型的应用
要 点 讲 解
要点 一次函数模型的应用
建立两个变量之间的函数关系,从实际问题中抽象出一次函数的模型,可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在坐标平面内描出相应的点(若干个).
(2)观察描出的点在坐标平面内的分布情况,从而推测函数图象的大致形状,并据此进一步猜想x与y之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验,必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
经典例题 某商店销售某种新型化工原料,其市场指导价是每千克160元(该商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.
(1)为了扩大销售量,该商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润.那么该商店调整价格后的标价是多少元?打折后的实际售价是多少元?
(2)该商店为了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:
实际售价x(元/千克)
…
150
160
170
180
…
月销售量y(千克)
…
500
480
460
440
…
①请你在所给的平面直角坐标系(如图)中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;
②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;
③若该商店某月按同一实际售价共卖出这种原料450千克,请你求出该商店这个月销售这种原料的利润是多少元.
解:(1)依题意知,每千克原料的进货价为160×75%=120(元).
设该商店调整价格后的标价为x元,则0.8x-120=0.8x×20%,解得x=187.5,187.5×0.8=150(元),所以调整价格后的标价是187.5元,打折后的实际售价是150元.
(2)①描点、画图,如图所示,观察图象,可知这些点的发展趋势近似是一条直线,所以猜想y与x之间存在着一次函数关系.
②根据①中的猜想,设y与x之间的函数表达式为y=kx+b(k≠0),将点(150,500)和(160,480)代入表达式,得解得
所以y与x之间的函数表达式为y=-2x+800.
将点(170,460)和(180,440)代入y=-2x+800,均成立,即这些点都符合y=-2x+800.所以y与x之间为一次函数关系.
所以①中猜想y与x之间存在着一次函数关系是正确的.
③设该商店这个月销售这种原料的利润为w元,
当y=450时,x=175,所以w=(175-120)×450=24750.答:该商店这个月销售这种原料的利润为24750元.
当 堂 检 测
1. 在某次实验中,测得两个变量m和v之间的4组对应数据如下表,则m和v之间的关系最接近于下列关系式中的( )
m
1
2
3
4
v
0.01
2.9
6.03
9.1
A. v=2m-2 B. v=2m-1
C. v=3m-3 D. v=m+1
2. 对于气温,有的地方用摄氏温度表示,有些地方用华氏温度表示,摄氏温度与华氏温度之间存在着某种函数关系,从温度计上可以看出摄氏温度x(℃)与华氏温度y()有如下表所示的对应关系,则确定y与x之间的函数关系是( )
x(℃)
…
-10
0
10
20
30
…
y()
…
14
32
50
68
86
…
A. y=x B. y=1.8x+32
C. y=0.56x2+7.4 x+32 D. y=2.1x+26
3. 为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在整个骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(米),则y与t(15
A. 小亮骑自行车的平均速度是12km/h B. 妈妈比小亮提前0.5h到达姥姥家
C. 妈妈在距家12km处追上小亮 D. 9:30妈妈追上小亮
第4题 第5题
5. 某种产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间的函数关系图象如图所示.则y与x之间的函数表达式是 .
6. 某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如下表:
时间t(天)
1
3
6
10
16
…
日销售量m(件)
94
90
84
76
64
…
通过认真分析上表的数据,用所学过的函数知识:
(1)确定满足这些数据的m(件)与t(天)之间的函数表达式;
(2)判断它是否符合预测函数模型.
7. 健身运动已成为时尚,某公司计划组装A,B两种型号的健身器材共40套,捐赠给社区健身中心.组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A,B两种型号的健身器材时,共有多少种组装方案;
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元.求总组装费用最少的组装方案,最少组装费用是多少?
当堂检测参考答案
1. C 2. B 3. B 4. D
5. y=3x+2
6. 解:(1)设m(件)与t(天)的函数模型为m=kt+b,将(1,94),(3,90)代入可求得k=-2,b=96,所以m=-2t+96.
(2)经检验,其它点的坐标均符合以上表达式,所以符合预测函数模型.
7. 解:(1)设该公司组装A型器材x套,则组装B型器材(40-x)套,依题意,得解得22≤x≤30.因为x为整数,所以x可取22,23,24,25,26,27,28,29,30.所以组装A,B两种型号的健身器材共有9种组装方案.
(2)总组装费用y=20x+18(40-x)=2x+720.因为k=2>0,所以y随x的增大而增大.所以当x=22时,总组装费用最少,总组装费用最少是2×22+720=764(元).所以总组装费用最少的组装方案是:组装A型器材22套,组装B型器材18套,最少组装费用是764元.
