新高考必修2辽宁地区专用 2.3.1 圆的标准方程27张
文档属性
| 名称 | 新高考必修2辽宁地区专用 2.3.1 圆的标准方程27张 |  | |
| 格式 | zip | ||
| 文件大小 | 923.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 19:26:26 | ||
图片预览








文档简介
课件27张PPT。第二章
平面解析几何初步2.3 圆的方程
2.3.1 圆的标准方程预习探究1.设圆的圆心坐标为(a,b),半径为r,则圆的标准方程是 .?
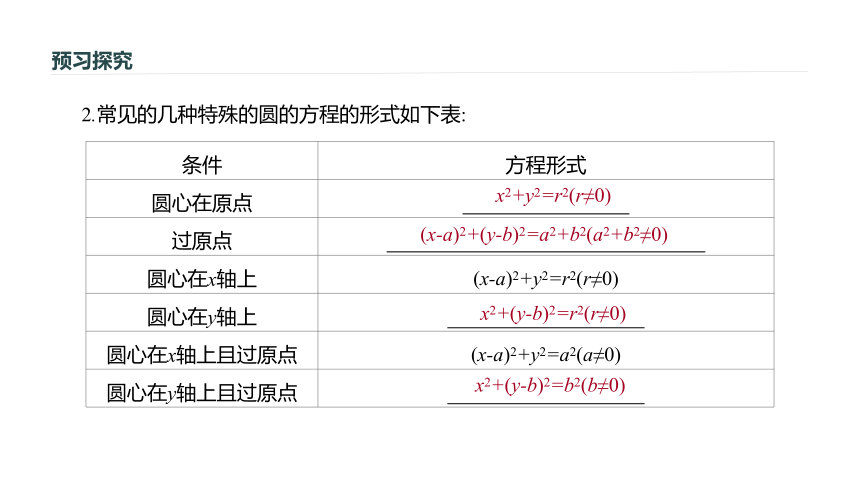
圆的标准方程的两个基本要素: 和 .它们分别确定了圆的位置和大小,从而确定了圆,所以只要a,b,r(r>0)三个量确定了,圆的方程就唯一确定了.?圆的标准方程知识点一(x-a)2+(y-b)2=r2圆心半径预习探究2.常见的几种特殊的圆的方程的形式如下表:x2+y2=r2(r≠0)(x-a)2+(y-b)2=a2+b2(a2+b2≠0)x2+(y-b)2=r2(r≠0)x2+(y-b)2=b2(b≠0)预习探究(续表)(x-a)2+(y-b)2=a2(a≠0)(x-a)2+(y-b)2=a2(|a|=|b|≠0)预习探究[探究] 下列说法正确的是 .?
①圆(x+2)2+(y+1)2=a2(a≠0)的圆心坐标为(2,1);
②方程(x+2)2+y2=25表示圆心坐标为(-2,0),面积为25π的圆;
③方程(x-2)2+(y-1)2=a2(a≠0)表示圆心坐标为(2,1),半径为a的圆;
④方程(x-3)2+(y+a)2=b2(b≠0)表示圆心坐标为(3,-a),半径为|b|的圆.②④预习探究已知点P(x0,y0),圆的标准方程为(x-a)2+(y-b)2=r2.
若点P在圆内,则有(x0-a)2+(y0-b)2 r2;?
若点P在圆上,则有(x0-a)2+(y0-b)2 r2;?
若点P在圆外,则有(x0-a)2+(y0-b)2 r2.?点与圆的位置关系知识点二<=>预习探究[探究] 试判断点(2,2)与圆x2+y2=4的位置关系.解:因为22+22=8>4,所在点(2,2)在圆x2+y2=4的外部.考点类析例1 (1)写出下列方程表示的圆的圆心和半径.
①x2+y2=2;②(x-3)2+y2=4;
③x2+(y-1)2=9;④(x+1)2+(y+2)2=8.
已知圆的标准方程,解决与圆心、半径有关的问题考点一?考点类析(2)①b=0.例1 (2)已知圆的方程为(x-a)2+(y-b)2=r2(r>0),试根据下列条件,分别写出a,b,r应满足的条件:
①圆心在x轴上;
②圆与y轴相切;
③圆过原点且与y轴相切;
④圆与两坐标轴均相切.②r=|a|(a≠0).③r=|a|(a≠0),b=0.④|a|=|b|=r(a≠0,b≠0).考点类析求圆的标准方程[导入] 求解圆的标准方程,本质是求解什么?解:求解圆的标准方程,本质就是求解圆心横坐标、纵坐标和半径三个量.考点二考点类析?x2+y2=25(x-2)2+(y-1)2=3(x-8)2+(y+3)2=25(x-1)2+(y+3)2=29(x-1)2+(y-1)2=4考点类析[解析] 设圆心坐标为(a,a),半径为R,由题意得(a-2)2+(a-2)2=(a-4)2+(a-2)2,解得a=3.
∴R2=(3-2)2+(3-2)2=2,故圆的标准方程为(x-3)2+(y-3)2=2.?A考点类析[小结] 求解圆的标准方程常见的方法有:(1)直接法,直接找出圆心、半径,写出方程;(2)待定系数法,设出圆的标准方程,根据题目条件列出关于a,b,r的方程组求解.考点类析点与圆的位置关系[导入] 如何判断点与圆的位置关系?解:先计算点到圆心的距离,再与半径比较大小即可确定.通常为了计算方便,直接比较二者平方的大小即可.考点三考点类析?例3 求过两点A(1,4),B(3,2),且圆心在直线y=0上的圆的标准方程,并判断点M1(2,3),
M2(2,4)与圆的位置关系.考点类析?考点类析[解析] (1)易知圆的圆心坐标为(2,3),因为(3-2)2+(2-3)2=2<4,所以点P(3,2)在圆内.变式 (1)已知圆的方程是(x-2)2+(y-3)2
=4,则点P(3,2)一定 ( )
A.是圆心 B.在圆上
C.在圆内 D.在圆外C?C?考点类析[小结] 点与圆的位置关系主要有三种题型:一是判断点与圆的位置关系,二是判断多点是否共圆,三是根据位置关系求参数的值.考点类析?拓展 已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,则实数a的取值范围为 .??考点类析圆的方程的应用[导入] 圆的方程主要有哪些应用?解:主要应用在拱桥、隧道、生活中的规划问题、区域问题等方面,利用其计算其中的数据.考点四考点类析例4 一座圆拱桥如图2-3-1所示,当水面在如图位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面的宽约为多少?(精确到0.01 m)图2-3-1?考点类析变式 已知某隧道的截面是半径为4 m的半圆,该隧道内设双行线公路,同方向只有一个车道,车辆只能在道路中心线右侧行驶,则一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?(假设货车顶部为平顶)?考点类析[小结] 圆的方程的应用关键是建立适当的直角坐标系求出圆的方程,然后将实际问题中的数据转化到圆中,利用圆的有关知识解决实际问题,需要注意最后要回扣原题,所求数据要符合实际意义.当堂自测??D当堂自测??D当堂自测[解析] 由题意可设圆心坐标为(a,a),a>0,则半径r=a,
∴圆的方程为(x-a)2+(y-a)2=a2.
又点A(1,2)在圆上,∴(1-a)2+(2-a)2=a2,解得a=1或a=5.
∴所求圆的方程为(x-1)2+(y-1)2=1或(x-5)2+(y-5)2=25.3.过点A(1,2),且与两坐标轴同时相切的圆的方程为 ( )
A.(x-1)2+(y-1)2=1或(x-5)2+(y-5)2=25
B.(x-1)2+(y-3)2=2
C.(x-5)2+(y-5)2=25
D.(x-1)2+(y-1)2=1A 当堂自测?4.圆心既在直线x-y=0上,又在直线x+y-4=0上,且经过原点的圆的方程是 .?(x-2)2+(y-2)2=8
平面解析几何初步2.3 圆的方程
2.3.1 圆的标准方程预习探究1.设圆的圆心坐标为(a,b),半径为r,则圆的标准方程是 .?
圆的标准方程的两个基本要素: 和 .它们分别确定了圆的位置和大小,从而确定了圆,所以只要a,b,r(r>0)三个量确定了,圆的方程就唯一确定了.?圆的标准方程知识点一(x-a)2+(y-b)2=r2圆心半径预习探究2.常见的几种特殊的圆的方程的形式如下表:x2+y2=r2(r≠0)(x-a)2+(y-b)2=a2+b2(a2+b2≠0)x2+(y-b)2=r2(r≠0)x2+(y-b)2=b2(b≠0)预习探究(续表)(x-a)2+(y-b)2=a2(a≠0)(x-a)2+(y-b)2=a2(|a|=|b|≠0)预习探究[探究] 下列说法正确的是 .?
①圆(x+2)2+(y+1)2=a2(a≠0)的圆心坐标为(2,1);
②方程(x+2)2+y2=25表示圆心坐标为(-2,0),面积为25π的圆;
③方程(x-2)2+(y-1)2=a2(a≠0)表示圆心坐标为(2,1),半径为a的圆;
④方程(x-3)2+(y+a)2=b2(b≠0)表示圆心坐标为(3,-a),半径为|b|的圆.②④预习探究已知点P(x0,y0),圆的标准方程为(x-a)2+(y-b)2=r2.
若点P在圆内,则有(x0-a)2+(y0-b)2 r2;?
若点P在圆上,则有(x0-a)2+(y0-b)2 r2;?
若点P在圆外,则有(x0-a)2+(y0-b)2 r2.?点与圆的位置关系知识点二<=>预习探究[探究] 试判断点(2,2)与圆x2+y2=4的位置关系.解:因为22+22=8>4,所在点(2,2)在圆x2+y2=4的外部.考点类析例1 (1)写出下列方程表示的圆的圆心和半径.
①x2+y2=2;②(x-3)2+y2=4;
③x2+(y-1)2=9;④(x+1)2+(y+2)2=8.
已知圆的标准方程,解决与圆心、半径有关的问题考点一?考点类析(2)①b=0.例1 (2)已知圆的方程为(x-a)2+(y-b)2=r2(r>0),试根据下列条件,分别写出a,b,r应满足的条件:
①圆心在x轴上;
②圆与y轴相切;
③圆过原点且与y轴相切;
④圆与两坐标轴均相切.②r=|a|(a≠0).③r=|a|(a≠0),b=0.④|a|=|b|=r(a≠0,b≠0).考点类析求圆的标准方程[导入] 求解圆的标准方程,本质是求解什么?解:求解圆的标准方程,本质就是求解圆心横坐标、纵坐标和半径三个量.考点二考点类析?x2+y2=25(x-2)2+(y-1)2=3(x-8)2+(y+3)2=25(x-1)2+(y+3)2=29(x-1)2+(y-1)2=4考点类析[解析] 设圆心坐标为(a,a),半径为R,由题意得(a-2)2+(a-2)2=(a-4)2+(a-2)2,解得a=3.
∴R2=(3-2)2+(3-2)2=2,故圆的标准方程为(x-3)2+(y-3)2=2.?A考点类析[小结] 求解圆的标准方程常见的方法有:(1)直接法,直接找出圆心、半径,写出方程;(2)待定系数法,设出圆的标准方程,根据题目条件列出关于a,b,r的方程组求解.考点类析点与圆的位置关系[导入] 如何判断点与圆的位置关系?解:先计算点到圆心的距离,再与半径比较大小即可确定.通常为了计算方便,直接比较二者平方的大小即可.考点三考点类析?例3 求过两点A(1,4),B(3,2),且圆心在直线y=0上的圆的标准方程,并判断点M1(2,3),
M2(2,4)与圆的位置关系.考点类析?考点类析[解析] (1)易知圆的圆心坐标为(2,3),因为(3-2)2+(2-3)2=2<4,所以点P(3,2)在圆内.变式 (1)已知圆的方程是(x-2)2+(y-3)2
=4,则点P(3,2)一定 ( )
A.是圆心 B.在圆上
C.在圆内 D.在圆外C?C?考点类析[小结] 点与圆的位置关系主要有三种题型:一是判断点与圆的位置关系,二是判断多点是否共圆,三是根据位置关系求参数的值.考点类析?拓展 已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,则实数a的取值范围为 .??考点类析圆的方程的应用[导入] 圆的方程主要有哪些应用?解:主要应用在拱桥、隧道、生活中的规划问题、区域问题等方面,利用其计算其中的数据.考点四考点类析例4 一座圆拱桥如图2-3-1所示,当水面在如图位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面的宽约为多少?(精确到0.01 m)图2-3-1?考点类析变式 已知某隧道的截面是半径为4 m的半圆,该隧道内设双行线公路,同方向只有一个车道,车辆只能在道路中心线右侧行驶,则一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?(假设货车顶部为平顶)?考点类析[小结] 圆的方程的应用关键是建立适当的直角坐标系求出圆的方程,然后将实际问题中的数据转化到圆中,利用圆的有关知识解决实际问题,需要注意最后要回扣原题,所求数据要符合实际意义.当堂自测??D当堂自测??D当堂自测[解析] 由题意可设圆心坐标为(a,a),a>0,则半径r=a,
∴圆的方程为(x-a)2+(y-a)2=a2.
又点A(1,2)在圆上,∴(1-a)2+(2-a)2=a2,解得a=1或a=5.
∴所求圆的方程为(x-1)2+(y-1)2=1或(x-5)2+(y-5)2=25.3.过点A(1,2),且与两坐标轴同时相切的圆的方程为 ( )
A.(x-1)2+(y-1)2=1或(x-5)2+(y-5)2=25
B.(x-1)2+(y-3)2=2
C.(x-5)2+(y-5)2=25
D.(x-1)2+(y-1)2=1A 当堂自测?4.圆心既在直线x-y=0上,又在直线x+y-4=0上,且经过原点的圆的方程是 .?(x-2)2+(y-2)2=8
