新高考必修2辽宁地区专用 本章总结提升30张
文档属性
| 名称 | 新高考必修2辽宁地区专用 本章总结提升30张 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 19:27:21 | ||
图片预览










文档简介
课件30张PPT。第二章
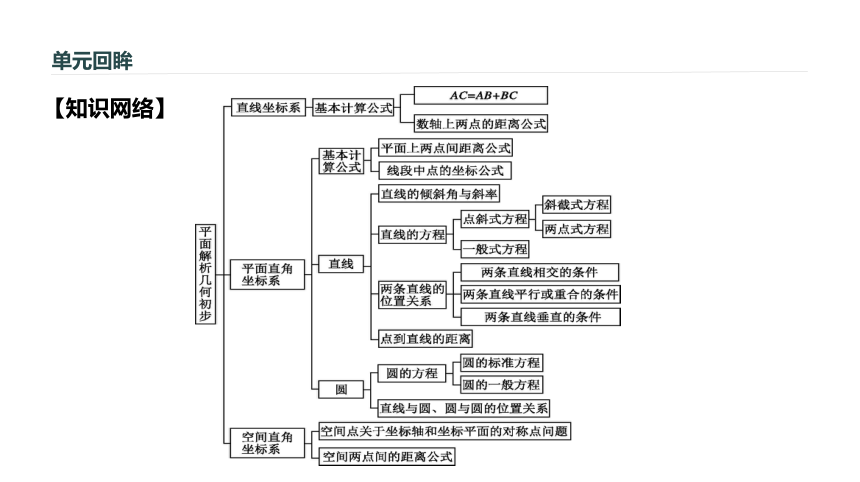
平面解析几何初步本章总结提升单元回眸【知识网络】单元回眸【知识辨析】判断下列说法是否正确.(请在括号中填“√”或“×”)
(1)直线的倾斜角越大,则斜率越大. ( )
(2)直线的斜率越大,则直线越陡. ( )
(3)两直线平行,则斜率相等. ( )×××[解析] (1)钝角比锐角大,但直线倾斜角为钝角时斜率为负,倾斜角为锐角时斜率为正.(2)当直线斜率为负数时,斜率越大,直线越平缓.(3)两直线平行时,若斜率都存在,则斜率相等.若两直线都平行于y轴,则它们的斜率不存在.单元回眸(4)两直线垂直,则斜率乘积等于-1. ( )
(5)过点P(x0,y0)的直线方程可设为
y-y0=k(x-x0). ( )
(6)圆(x-a)2+(y-b)2=m2的半径为m. ( )
(7)方程x2+y2+Dx+Ey+F=0表示圆的条件是D2+E2-4F>0. ( )
(8)若圆心到直线的距离小于半径,则直线与圆相交. ( )×××√√(4)两直线垂直,若斜率都存在,则斜率乘积等于-1;当一条直线斜率为0,另一条直线斜率不存在时也满足两直线垂直.(5)过点P(x0,y0)的直线的斜率存在时才可设其方程为y-y0=k(x-x0).(6)圆(x-a)2+(y-b)2=m2的半径为|m|.单元回眸(9)已知圆x2+y2=r2,则过点P(x0,y0)的圆的切线方程为x0x+y0y=r2. ( )
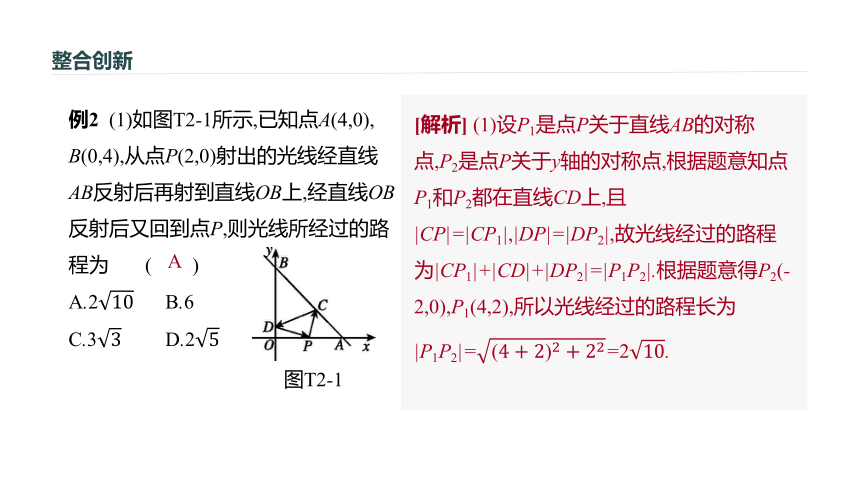
(10)两圆方程相减消去二次项,所得直线方程表示两圆的公共弦所在直线的方程.( )××(9)当点P(x0,y0)在圆x2+y2=r2上时,过点P的切线方程才为x0x+y0y=r2.(10)当两圆相交时,两圆方程相减消去二次项,所得直线方程才是公共弦所在直线的方程.整合创新直线的倾斜角与斜率以及直线方程问题[类型总述] (1)直线方程的求解;(2)直线的几种方程的应用;(3)直线的倾斜角和斜率的关系及求解.题型一整合创新例1 若过点A(0,-1)的直线l与圆C:x2+(y-1)2=1有公共点,求直线l的倾斜角的取值范围.?整合创新??整合创新直线与直线的位置关系问题[类型总述] (1)点到直线的距离公式及两平行线间的距离公式的应用;(2)直线与直线位置关系的判断和应用.题型二整合创新?A?图T2-1整合创新例2 (2)[2018·北京卷] 在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m变化时,d的最大值为 ( )
A.1 B.2 C.3 D.4?C整合创新例2 (2)[2018·北京卷] 在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m变化时,d的最大值为 ( )
A.1 B.2 C.3 D.4C方法二:该题考查圆周上一点到动直线的距离的最值问题,由题知动直线过定点(2,0),观察下图可知,所求距离的最大值为点(2,0)到单位圆上点的距离的最大值,故为3.整合创新变式 光线从点(-1,3)射向x轴,经过x轴反射后过点(4,6),则反射光线所在直线的方程是 .?9x-5y-6=0整合创新圆的方程的求解问题[类型总述] (1)圆的方程的求解;(2)二元二次方程表示圆的条件;(3)圆的方程的简单应用.题型三整合创新??B整合创新例3 (2)[2018·天津卷] 在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .?(2)易知所求圆的圆心既在直线x+y=1上,也在直线x=1上,故圆心坐标为(1,0),进而可得该圆的半径为1,所以所求圆的方程为(x-1)2+y2=1,即x2+y2-2x=0.x2+y2-2x=0整合创新??A整合创新直线与圆的位置关系问题[类型总述] (1)直线与圆的位置关系的判断;(2)利用直线与圆的位置关系的判断方法求解弦长、圆的切线长、直线斜率、参数范围等.题型四整合创新??A整合创新例4 (2)[2018·全国卷Ⅰ] 直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .???整合创新??D整合创新??C整合创新??整合创新??整合创新??整合创新圆与圆的位置关系问题[类型总述] (1)圆与圆位置关系的判断和应用;(2)两圆相交的公共弦问题.题型五整合创新?A?整合创新例6 (2)已知圆x2+y2=10和圆(x-1)2+(y-3)2=20相交于A,B两点,则直线AB的方程是 .?(2)圆(x-1)2+(y-3)2=20可化为x2+y2-2x-6y-10=0,两个圆的方程相减可得-2x-6y=0,即x+3y=0,即为直线AB的方程.x+3y=0整合创新变式 (1)圆O1:x2+y2-2x-2y=0和圆O2: x2+y2-4y=0的位置关系是 .??相交整合创新变式 (2)与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是 .?
?(x-2)2+(y-2)2=2
平面解析几何初步本章总结提升单元回眸【知识网络】单元回眸【知识辨析】判断下列说法是否正确.(请在括号中填“√”或“×”)
(1)直线的倾斜角越大,则斜率越大. ( )
(2)直线的斜率越大,则直线越陡. ( )
(3)两直线平行,则斜率相等. ( )×××[解析] (1)钝角比锐角大,但直线倾斜角为钝角时斜率为负,倾斜角为锐角时斜率为正.(2)当直线斜率为负数时,斜率越大,直线越平缓.(3)两直线平行时,若斜率都存在,则斜率相等.若两直线都平行于y轴,则它们的斜率不存在.单元回眸(4)两直线垂直,则斜率乘积等于-1. ( )
(5)过点P(x0,y0)的直线方程可设为
y-y0=k(x-x0). ( )
(6)圆(x-a)2+(y-b)2=m2的半径为m. ( )
(7)方程x2+y2+Dx+Ey+F=0表示圆的条件是D2+E2-4F>0. ( )
(8)若圆心到直线的距离小于半径,则直线与圆相交. ( )×××√√(4)两直线垂直,若斜率都存在,则斜率乘积等于-1;当一条直线斜率为0,另一条直线斜率不存在时也满足两直线垂直.(5)过点P(x0,y0)的直线的斜率存在时才可设其方程为y-y0=k(x-x0).(6)圆(x-a)2+(y-b)2=m2的半径为|m|.单元回眸(9)已知圆x2+y2=r2,则过点P(x0,y0)的圆的切线方程为x0x+y0y=r2. ( )
(10)两圆方程相减消去二次项,所得直线方程表示两圆的公共弦所在直线的方程.( )××(9)当点P(x0,y0)在圆x2+y2=r2上时,过点P的切线方程才为x0x+y0y=r2.(10)当两圆相交时,两圆方程相减消去二次项,所得直线方程才是公共弦所在直线的方程.整合创新直线的倾斜角与斜率以及直线方程问题[类型总述] (1)直线方程的求解;(2)直线的几种方程的应用;(3)直线的倾斜角和斜率的关系及求解.题型一整合创新例1 若过点A(0,-1)的直线l与圆C:x2+(y-1)2=1有公共点,求直线l的倾斜角的取值范围.?整合创新??整合创新直线与直线的位置关系问题[类型总述] (1)点到直线的距离公式及两平行线间的距离公式的应用;(2)直线与直线位置关系的判断和应用.题型二整合创新?A?图T2-1整合创新例2 (2)[2018·北京卷] 在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m变化时,d的最大值为 ( )
A.1 B.2 C.3 D.4?C整合创新例2 (2)[2018·北京卷] 在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m变化时,d的最大值为 ( )
A.1 B.2 C.3 D.4C方法二:该题考查圆周上一点到动直线的距离的最值问题,由题知动直线过定点(2,0),观察下图可知,所求距离的最大值为点(2,0)到单位圆上点的距离的最大值,故为3.整合创新变式 光线从点(-1,3)射向x轴,经过x轴反射后过点(4,6),则反射光线所在直线的方程是 .?9x-5y-6=0整合创新圆的方程的求解问题[类型总述] (1)圆的方程的求解;(2)二元二次方程表示圆的条件;(3)圆的方程的简单应用.题型三整合创新??B整合创新例3 (2)[2018·天津卷] 在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .?(2)易知所求圆的圆心既在直线x+y=1上,也在直线x=1上,故圆心坐标为(1,0),进而可得该圆的半径为1,所以所求圆的方程为(x-1)2+y2=1,即x2+y2-2x=0.x2+y2-2x=0整合创新??A整合创新直线与圆的位置关系问题[类型总述] (1)直线与圆的位置关系的判断;(2)利用直线与圆的位置关系的判断方法求解弦长、圆的切线长、直线斜率、参数范围等.题型四整合创新??A整合创新例4 (2)[2018·全国卷Ⅰ] 直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .???整合创新??D整合创新??C整合创新??整合创新??整合创新??整合创新圆与圆的位置关系问题[类型总述] (1)圆与圆位置关系的判断和应用;(2)两圆相交的公共弦问题.题型五整合创新?A?整合创新例6 (2)已知圆x2+y2=10和圆(x-1)2+(y-3)2=20相交于A,B两点,则直线AB的方程是 .?(2)圆(x-1)2+(y-3)2=20可化为x2+y2-2x-6y-10=0,两个圆的方程相减可得-2x-6y=0,即x+3y=0,即为直线AB的方程.x+3y=0整合创新变式 (1)圆O1:x2+y2-2x-2y=0和圆O2: x2+y2-4y=0的位置关系是 .??相交整合创新变式 (2)与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是 .?
?(x-2)2+(y-2)2=2
