新高考必修2辽宁地区专用 2.2.1 直线方程的概念与直线的斜率27张
文档属性
| 名称 | 新高考必修2辽宁地区专用 2.2.1 直线方程的概念与直线的斜率27张 |  | |
| 格式 | zip | ||
| 文件大小 | 941.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 19:20:52 | ||
图片预览








文档简介
课件27张PPT。第二章
平面解析几何初步2.2 直线的方程
2.2.1 直线方程的概念与直线的斜率预习探究一般地,如果以 为坐标的点都在某条直线上,且这条直线上点的坐标都是 ,那么这个方程叫作这条直线的方程,这条直线叫作这个方程的直线.?直线的方程与方程的直线定义知识点一一个方程的解这个方程的解预习探究[探究] 画出方程y=2x+1表示的直线.?预习探究直线的斜率知识点二1.直线斜率的定义
我们把直线y=kx+b中的 叫作这条直线的斜率.?
2.斜率公式
经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式是 .?
对于斜率公式,要注意下面三点:系数k?预习探究(1)k与P1,P2的顺序无关, 即y1,y2和x1,x2在公式中的前后次序可以 , 但分子与分母不能交换; ?
(2)当x1=x2时,公式右边无意义,直线与x轴 ,直线的斜率 ;?
(3)当y1=y2时, 直线与x轴 ,斜率k= .?同时交换垂直不存在平行或重合0预习探究[探究] m为何值时,经过A(m,0),B(-5,1-m)两点的直线AB的斜率是-1??预习探究直线的倾斜角知识点三1.定义:? 叫作这条直线的倾斜角,记为α.特别地,当 时,我们规定它的倾斜角为零度角,因此,倾斜角的取值范围是 .?
用运动变化的观点来看,直线的倾斜角是由x轴按逆时针方向旋转到与直线重合时所形成的角.
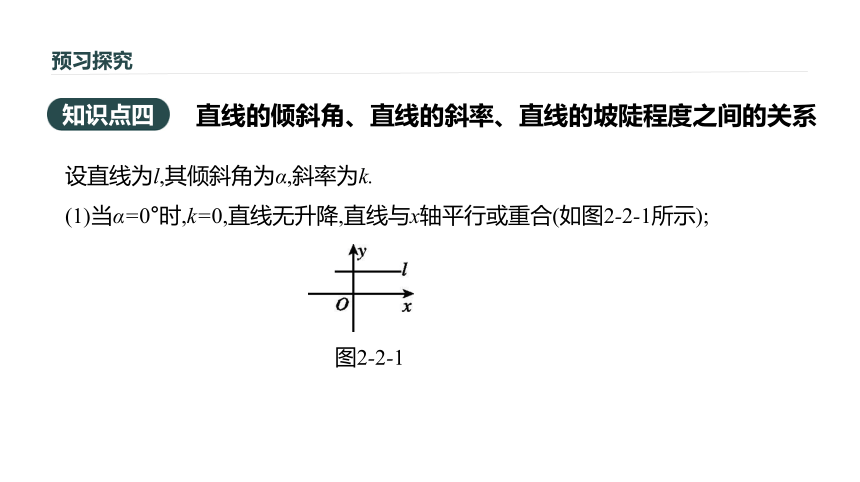
2.所有的直线都有 ,但不是所有的直线都有 ,倾斜角是90°的直线 斜率.x轴正向与直线向上的方向所成的角直线与x轴平行或重合0°≤α<180°倾斜角斜率没有预习探究[探究] 直线y=x的倾斜角为 ;直线y=3的倾斜角为 ;直线x=3的倾斜角为 .?45°0°90°预习探究直线的倾斜角、直线的斜率、直线的坡陡程度之间的关系知识点四图2-2-1设直线为l,其倾斜角为α,斜率为k.
(1)当α=0°时,k=0,直线无升降,直线与x轴平行或重合(如图2-2-1所示);预习探究图2-2-2图2-2-3图2-2-4(2)当0°<α<90°时,k>0,直线从左向右上升,α越大,k越大,直线越陡(如图2-2-2所示);
(3)当α=90°时,k不存在,直线与x轴垂直(如图2-2-3所示);
(4)当90°<α<180°时,k<0,直线从左向右下降,α越大,k越大,直线越平缓(如图2-2-4所示).预习探究[探究] 图2-2-5中三条直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系为 .?k1A.1 B.2 C.3 D.4A当堂自测[解析] ∵0°≤α<180°,∴分两种情况讨论.
当0°≤α<135°时,如图①所示,此时l1的倾斜角为α+45°;
当135°≤α<180°时,如图②所示,此时l1的倾斜角为45°+α-180°=α-135°.故选D.2.设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么下列对直线l1的倾斜角的说法正确的为 ( )
A.倾斜角为α+45°
B.倾斜角为α-135°
C.倾斜角为135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°D当堂自测??C当堂自测4.若经过点A(1-t,1+t)和点B(3,2t)的直线的倾斜角为钝角,则实数t的取值范围是 .?(-2,1)?当堂自测5.若过点A(2,-1)与B(a,1)的直线的倾斜角为锐角,则a的取值范围是 .??(2,+∞)
平面解析几何初步2.2 直线的方程
2.2.1 直线方程的概念与直线的斜率预习探究一般地,如果以 为坐标的点都在某条直线上,且这条直线上点的坐标都是 ,那么这个方程叫作这条直线的方程,这条直线叫作这个方程的直线.?直线的方程与方程的直线定义知识点一一个方程的解这个方程的解预习探究[探究] 画出方程y=2x+1表示的直线.?预习探究直线的斜率知识点二1.直线斜率的定义
我们把直线y=kx+b中的 叫作这条直线的斜率.?
2.斜率公式
经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式是 .?
对于斜率公式,要注意下面三点:系数k?预习探究(1)k与P1,P2的顺序无关, 即y1,y2和x1,x2在公式中的前后次序可以 , 但分子与分母不能交换; ?
(2)当x1=x2时,公式右边无意义,直线与x轴 ,直线的斜率 ;?
(3)当y1=y2时, 直线与x轴 ,斜率k= .?同时交换垂直不存在平行或重合0预习探究[探究] m为何值时,经过A(m,0),B(-5,1-m)两点的直线AB的斜率是-1??预习探究直线的倾斜角知识点三1.定义:? 叫作这条直线的倾斜角,记为α.特别地,当 时,我们规定它的倾斜角为零度角,因此,倾斜角的取值范围是 .?
用运动变化的观点来看,直线的倾斜角是由x轴按逆时针方向旋转到与直线重合时所形成的角.
2.所有的直线都有 ,但不是所有的直线都有 ,倾斜角是90°的直线 斜率.x轴正向与直线向上的方向所成的角直线与x轴平行或重合0°≤α<180°倾斜角斜率没有预习探究[探究] 直线y=x的倾斜角为 ;直线y=3的倾斜角为 ;直线x=3的倾斜角为 .?45°0°90°预习探究直线的倾斜角、直线的斜率、直线的坡陡程度之间的关系知识点四图2-2-1设直线为l,其倾斜角为α,斜率为k.
(1)当α=0°时,k=0,直线无升降,直线与x轴平行或重合(如图2-2-1所示);预习探究图2-2-2图2-2-3图2-2-4(2)当0°<α<90°时,k>0,直线从左向右上升,α越大,k越大,直线越陡(如图2-2-2所示);
(3)当α=90°时,k不存在,直线与x轴垂直(如图2-2-3所示);
(4)当90°<α<180°时,k<0,直线从左向右下降,α越大,k越大,直线越平缓(如图2-2-4所示).预习探究[探究] 图2-2-5中三条直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系为 .?k1
当0°≤α<135°时,如图①所示,此时l1的倾斜角为α+45°;
当135°≤α<180°时,如图②所示,此时l1的倾斜角为45°+α-180°=α-135°.故选D.2.设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么下列对直线l1的倾斜角的说法正确的为 ( )
A.倾斜角为α+45°
B.倾斜角为α-135°
C.倾斜角为135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°D当堂自测??C当堂自测4.若经过点A(1-t,1+t)和点B(3,2t)的直线的倾斜角为钝角,则实数t的取值范围是 .?(-2,1)?当堂自测5.若过点A(2,-1)与B(a,1)的直线的倾斜角为锐角,则a的取值范围是 .??(2,+∞)
