湘教版数学1.3反比例函数的应用课件(15张ppt)
文档属性
| 名称 | 湘教版数学1.3反比例函数的应用课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
1.3 反比例函数的应用
复习回顾
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大.
某校科技小组在一次野外考察途中,遇到一片烂泥湿地.为了安全、迅速地通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利通过了这片湿地.
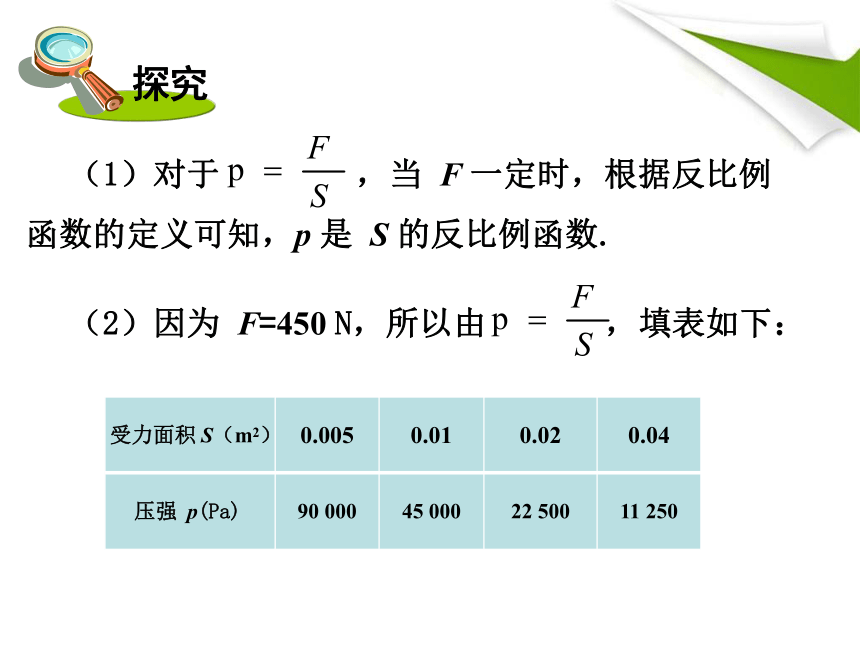
(2)若人对地面的压力 F=450 N,完成下表:
(3)当 F=450 N 时,试画出该函数的图象,并结合图象分析当受力面积 S 增大时,地面所受压强 p是如何变化的.据此,请说出他们铺垫木板(木板受力忽略不计)通过湿地的道理.
受力面积 S(m2) 0.005 0.01 0.02 0.04
压强 p(Pa)
受力面积 S(m2) 0.005 0.01 0.02 0.04
压强 p(Pa) 90 000 45 000 22 500 11 250
已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220V.
(1)写出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200Ω,则通过它的电流是多少?
(3)如果该电路接入的是一个滑动变阻器,怎样调整电阻R,就可以使电路中的电流I增大?
由于该电路的电压U为定值, 即该电路的电阻R与电流I的乘积为定值,因此该电路的电阻R与电流I成反比例函数关系.
(3)根据反比例函数的图象及性质可知,当滑动变阻器的电阻R减小时,就可以使电路中的电流I增大.
1.A、B两城市相距720千米,一列火车从A城去B城.
(2)若到达目的地后,按原路匀速原回,并要求在3小时内回到A城,则返回的速度不能低于____________
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是_____
240千米/小时.
3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为( )
A
4.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;
30
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
有效,因为燃烧时第4分钟含药量开始高于3毫克,当到第16分钟含药量开始低于3毫克,这样含药量不低于3毫克的时间共有16-4=12分钟,故有效.
【答案】
1.3 反比例函数的应用
复习回顾
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大.
某校科技小组在一次野外考察途中,遇到一片烂泥湿地.为了安全、迅速地通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利通过了这片湿地.
(2)若人对地面的压力 F=450 N,完成下表:
(3)当 F=450 N 时,试画出该函数的图象,并结合图象分析当受力面积 S 增大时,地面所受压强 p是如何变化的.据此,请说出他们铺垫木板(木板受力忽略不计)通过湿地的道理.
受力面积 S(m2) 0.005 0.01 0.02 0.04
压强 p(Pa)
受力面积 S(m2) 0.005 0.01 0.02 0.04
压强 p(Pa) 90 000 45 000 22 500 11 250
已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220V.
(1)写出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200Ω,则通过它的电流是多少?
(3)如果该电路接入的是一个滑动变阻器,怎样调整电阻R,就可以使电路中的电流I增大?
由于该电路的电压U为定值, 即该电路的电阻R与电流I的乘积为定值,因此该电路的电阻R与电流I成反比例函数关系.
(3)根据反比例函数的图象及性质可知,当滑动变阻器的电阻R减小时,就可以使电路中的电流I增大.
1.A、B两城市相距720千米,一列火车从A城去B城.
(2)若到达目的地后,按原路匀速原回,并要求在3小时内回到A城,则返回的速度不能低于____________
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是_____
240千米/小时.
3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为( )
A
4.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;
30
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
有效,因为燃烧时第4分钟含药量开始高于3毫克,当到第16分钟含药量开始低于3毫克,这样含药量不低于3毫克的时间共有16-4=12分钟,故有效.
【答案】
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
