12.2.1 用“SSS”判定三角形全等同步练习(含答案)
文档属性
| 名称 | 12.2.1 用“SSS”判定三角形全等同步练习(含答案) | 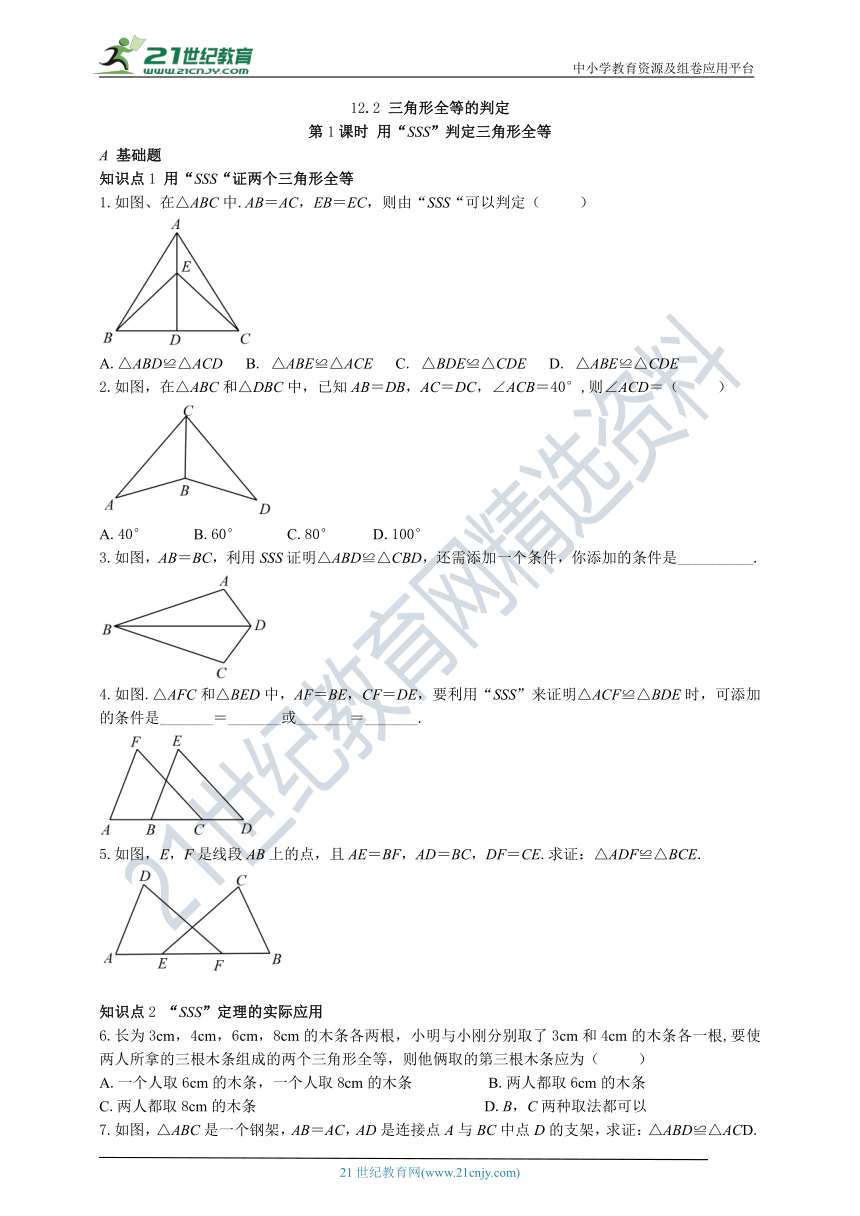 | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 15:26:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.2 三角形全等的判定
第1课时 用“SSS”判定三角形全等
A 基础题
知识点1 用“SSS“证两个三角形全等
1.如图、在△ABC中.AB=AC,EB=EC,则由“SSS“可以判定( )
A.△ABD≌△ACD? B. △ABE≌△ACE? C. △BDE≌△CDE? D. △ABE≌△CDE
2.如图,在△ABC和△DBC中,已知AB=DB,AC=DC,∠ACB=40°,则∠ACD=( )
A.40° B.60° C.80° D.100°
3.如图,AB=BC,利用SSS证明△ABD≌△CBD,还需添加一个条件,你添加的条件是__________.
4.如图.△AFC和△BED中,AF=BE,CF=DE,要利用“SSS”来证明△ACF≌△BDE时,可添加的条件是_______=_______或_______=_______.
5.如图,E,F是线段AB上的点,且AE=BF,AD=BC,DF=CE.求证:△ADF≌△BCE.
知识点2 “SSS”定理的实际应用
6.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的木条各一根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条 B.两人都取6cm的木条
C.两人都取8cm的木条 D.B,C两种取法都可以
7.如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证:△ABD≌△ACD.
B 提升题
8.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD=( )
A.120° B.125° C.127° D.104°
9.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证明△ACE≌△BDF时,需增加一个条件,这个条件可以是( )
A.AB=BC B.DC=BC C.AC=BD D.AB=BD
10.如图,AB=AC,BD=CD,求证:∠1=∠2.
11.如图,已知AB=AC,DB=EC,AD=AE,∠1=20°,求∠2的度数.
12.如图,已知AB=AC,AE=AD,BE=CD.
(1)求证:∠BAE=∠CAD;
(2)探究∠1,∠2,∠3之间的数量关系,并予以证明.
C 拓展题
13.已知AB=AC,AD=AE,BD=CE,且B、D、E三点在一条直线上.
(1)如图1,若B在线段DE上,求证:∠DAE=∠BAC;
(2)如图2,点B在ED的延长线上,请直接写出∠ADE与∠AEC之间的数量关系为.
(3)若点B在线段DE的延长线上(点ADE按逆时针排列),请将备用图补充完整,并直接写出∠ADE与∠AEC之间的数量关系为
参考答案
A基础题
1.B
2.C
3.AD=CD
4.AC BD AB CD
5.证明:∵AE=BF,∴AE+EF=BF+EF,即AF=BE.
在△ADF和△BCE中,
.
∴△ADF≌△BCE(SSS)
6.B
7.∵D为BC的中点,∴BD=CD
在△ABD与△ACD中.
∴△ABD≌△ACD(SSS)
B提升题
8.C
9.C
10.证明:略.
11.解:证△EAAC≌△DAB(SSS),∴∠EAC=∠DAB,∠EAC-∠BAC=∠DAB-∠BAC,即∠2=∠1=20°
12.证明:(1)△ABE≌△ACD(SSS);
(2)∠3=∠1-∠2
C拓展题
13.证:(1)证△ADB≌△AEC(SSS).
(2)证△ADB≌△AEC(SSS),∴∠ADB=∠AEC,∵∠ADE+∠ADB=180°∴∠ADE+∠AEC=180°.
(3)画图略,∠ADE=∠AEC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
