13.1.1 轴对称 同步练习(解析版)
图片预览

文档简介
初中数学人教版八年级上学期 第十三章 13.1.1 轴对称
一、基础巩固
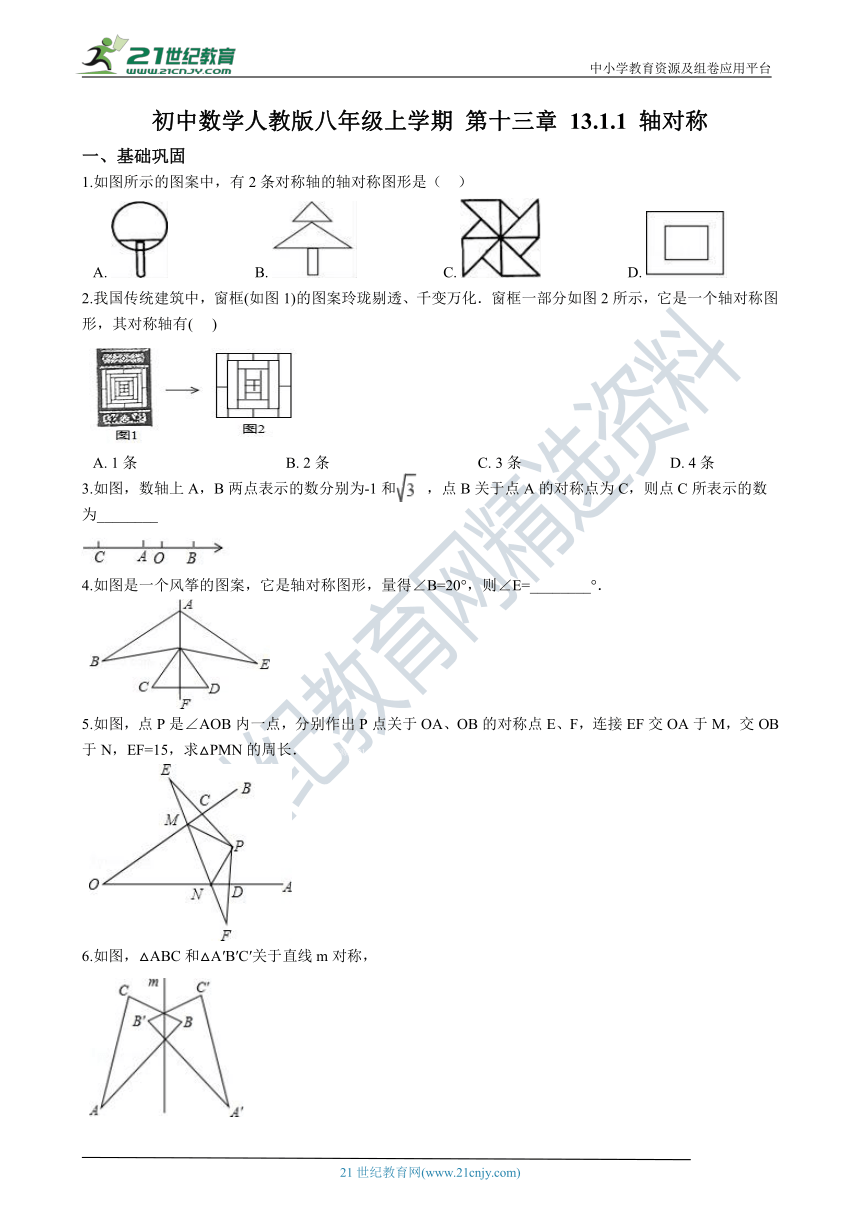
1.如图所示的图案中,有2条对称轴的轴对称图形是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化.窗框一部分如图2所示,它是一个轴对称图形,其对称轴有(??? ) 21cnjy.com
A.?1条???????????????????????????????????????B.?2条???????????????????????????????????????C.?3条???????????????????????????????????????D.?4条
3.如图,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,则点C所表示的数
为________ 2·1·c·n·j·y
4.如图是一个风筝的图案,它是轴对称图形,量得∠B=20°,则∠E=________°.
5.如图,点P是∠AOB内一点,分别作出P点关于OA、OB的对称点E、F,连接EF交OA于M,交OB于N,EF=15,求△PMN的周长. 【来源:21·世纪·教育·网】
6.如图,△ABC和△A′B′C′关于直线m对称,
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样关系?
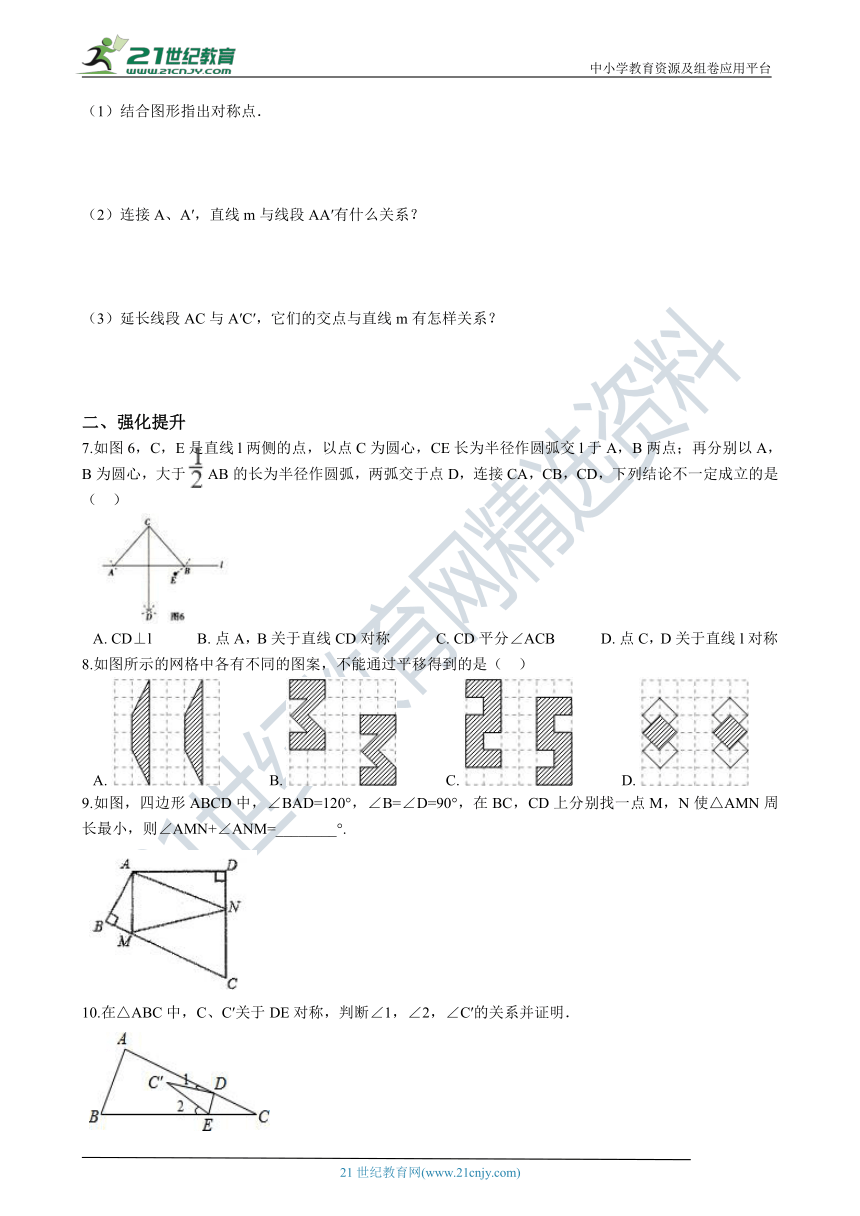
二、强化提升
7.如图6,C,E是直线l两侧的点,以点C为圆心,CE长为半径作圆弧交l于A,B两点;再分别以A,B为圆心,大于 AB的长为半径作圆弧,两弧交于点D,连接CA,CB,CD,下列结论不一定成立的是( ??) 21世纪教育网版权所有
A.?CD⊥l????????????B.?点A,B关于直线CD对称????????????C.?CD平分∠ACB????????????D.?点C,D关于直线l对称
8.如图所示的网格中各有不同的图案,不能通过平移得到的是(?? )
A.??????????????B.??????????????C.??????????????D.?
9.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM=________°. 21·世纪*教育网
10.在△ABC中,C、C′关于DE对称,判断∠1,∠2,∠C′的关系并证明.
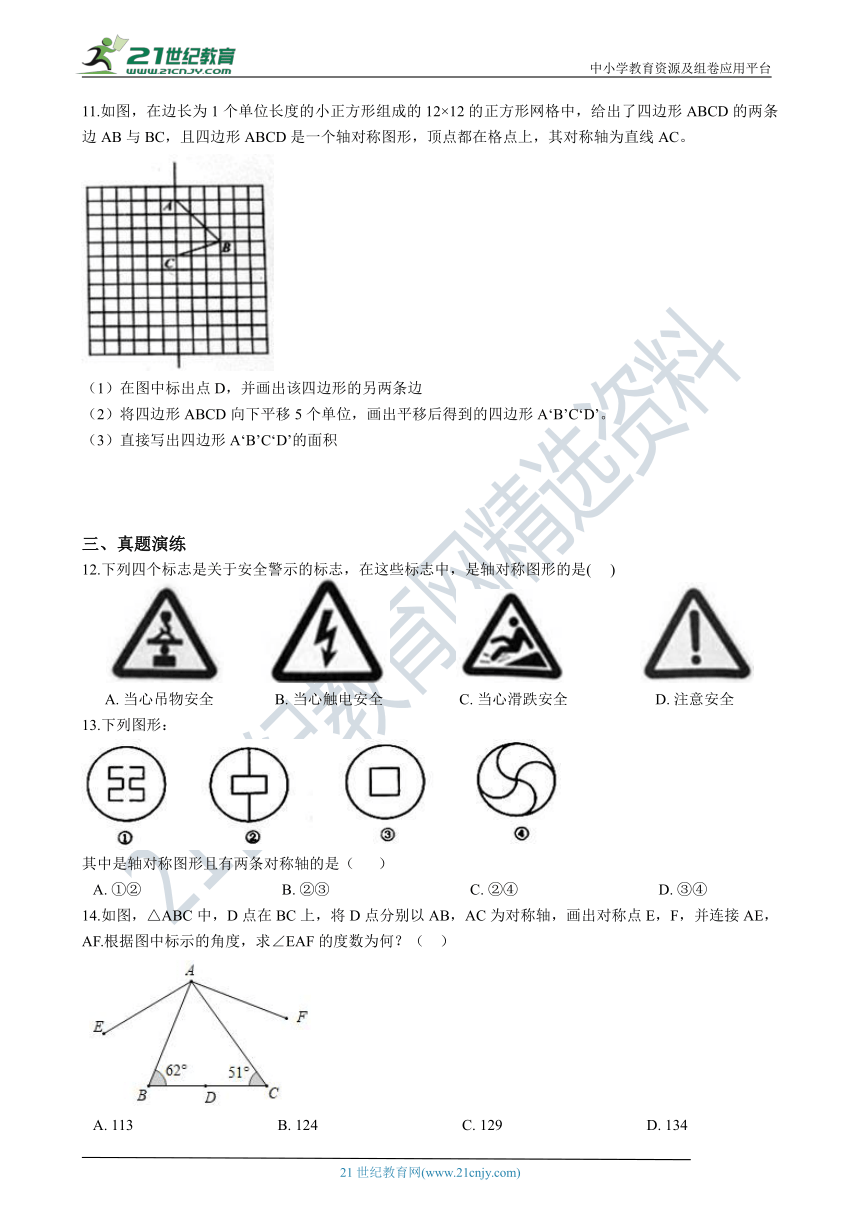
11.如图,在边长为1个单位长度的小正方形组成的12×12的正方形网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,顶点都在格点上,其对称轴为直线AC。
(1)在图中标出点D,并画出该四边形的另两条边
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A‘B’C‘D’。
(3)直接写出四边形A‘B’C‘D’的面积
三、真题演练
12.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是(??? )
A.?当心吊物安全????????????????B.?当心触电安全 C.?当心滑跌安全???????????????????????D.?注意安全
13.下列图形:
其中是轴对称图形且有两条对称轴的是(???? )
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
14.如图,△ABC中,D点在BC上,将D点分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,求∠EAF的度数为何?(?? ) 【出处:21教育名师】
A.?113??????????????????????????????????????B.?124??????????????????????????????????????C.?129??????????????????????????????????????D.?134
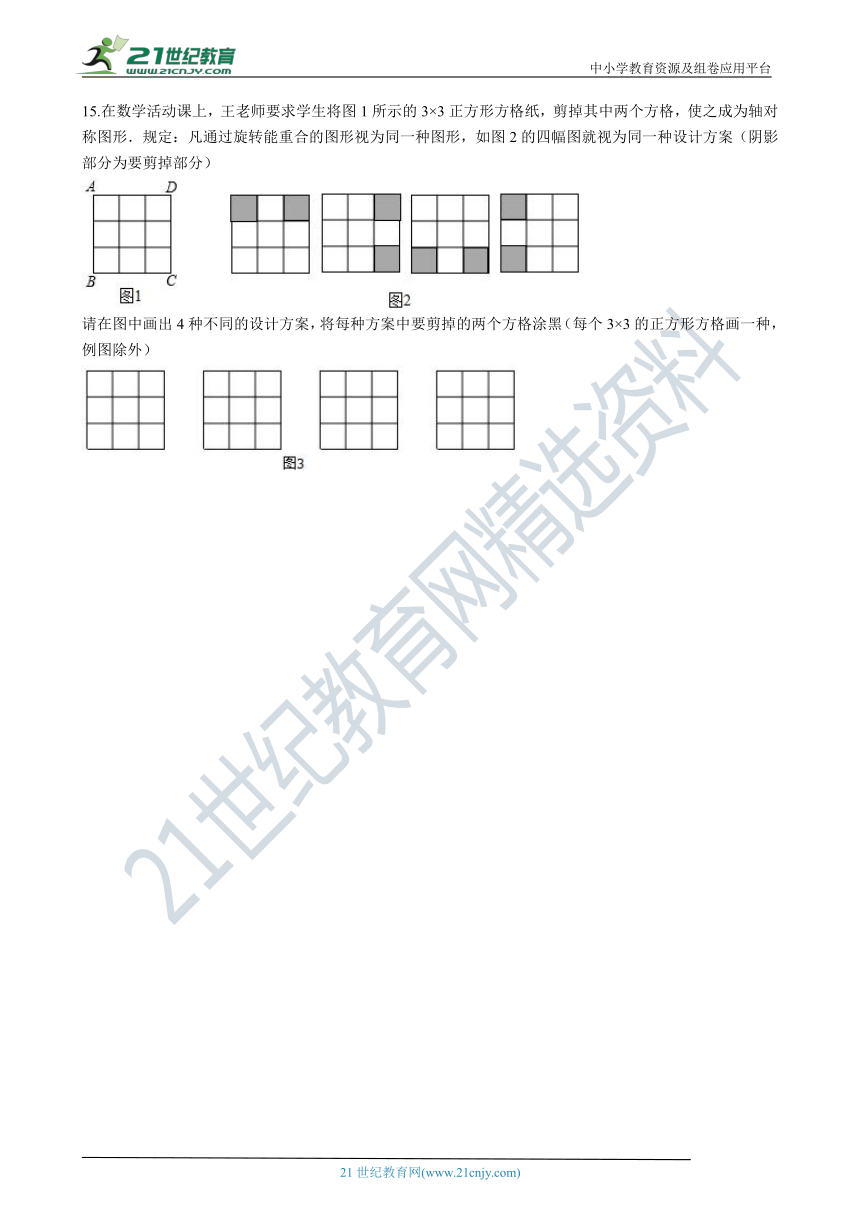
15.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
答案解析部分
一、基础巩固
1. D
解析:A、B各有一条对称轴,故不正确;
C没有对称轴,故不正确;
D有两条对称轴,故正确;
故答案为:D. 【分析】如果两个图形关于某条直线对称,那么这条直线就是对称轴。由对称轴的定义可知:A、B各有一条对称轴;C没有对称轴;D有两条对称轴。2-1-c-n-j-y
2. B
解析:过窗框相对两边中点所在直线折叠,直线两旁的部分就能完全重合,故窗框的对称轴有两条。故答案为:B。
【分析】把一个平面图形沿着某一条直线折叠,直线两旁的部分能完全重合的几何图形就是轴对称图形;沿着对折的这条直线就是轴对称图形的对称轴,由于该图案过窗框相对两边中点所在直线折叠,直线两旁的部分就能完全重合,故窗框的对称轴有两条。
3. - -2
解析:∵ 数轴上A,B两点表示的数分别为-1和 , ∴AB=-(-1)=+1 点B关于点A的对称点为C, ∴AC=AB=+1 ∴点C所表示的数-1-(+1)= 故答案为:
【分析】根据点A、B的坐标求出AB的长,再根据轴对称的性质,由点B关于点A的对称点为C,可知AC=AB,就可求出AC的长,然后就可确定出点C所表示的数。
4. 20
解析:∵风筝的图案是轴对称图形,
∴∠E=∠B=20°.
故答案为:20.
【分析】根据轴对称图形的性质得∠E=∠B,即可求得.
5. 解:∵P点关于OA、OB的对称点分别为E、F,
∴PM=EM,PN=FN,
∴△PMN的周长=PM+MN+FN=ME+MN+FN=EF,
∵EF=15,
∴△PMN的周长=15.
【分析】根据轴对称的性质“ 如果两个图形关于某条直线对称,那么 对称轴是任何一对对应点所连 线段的垂直平分线”可得 PM=EM,PN=FN, 由图可得 △PMN的周长=PM+MN+FN=ME+MN+FN=EF。
6. (1)解:由图可知,对称点有A和A′,B和B′,C和C′ (2)解:连接AA′,直线m是线段AA′的垂直平分线; (3)解:延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或其延长线的交点在对称轴上.
【分析】(1)根据对称图形的性质和△ABC和△A′B′C′关于直线m对称,可得对称点; (2)根据“对称轴是两个对称点的连线的垂直平分线”可得答案; (3)根据轴对称的性质可直接得出结论.【版权所有:21教育】
二、强化提升
7. D
解析:连接AD,BD, ∵AC=BC,AD=BD,CD=CD ∴△ACD≌△BCD(SSS) ∴∠ACD=∠BCD, ∵AC=BC, ∴CD⊥AB,AO=BO, ∴CD垂直l, 点A,B关于直线CD对称 ,故A、B、C不符合题意; ∵CO与DO不一定相等, ∴C、D不一定关于直线l对称,故D符合题意; 故答案为:D. 【分析】根据“SSS”可证△ACD≌△BCD,可得∠ACD=∠BCD,利用等腰三角形三线合一的性质可得CD⊥AB,AO=BO,据此判断A、B、C;由于CO与DO不一定相等,据此可判断D.
8. C
解析: A、可以通过平移得到,不符合题意;
B、可以通过平移得到,不符合题意;
C、先利用轴对称,再通过平移得到,符合题意;
D、可以通过平移得到,不符合题意.
故答案为:C
【分析】平移是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动, 简称平移。根据定义即可判断求解。www.21-cn-jy.com
9. 120
解析:作点A关于BC的对称点G,作点A关于DC的对称点H,连接HG,分别交BC、DC于点M、N。连接AM、AN。则AM=GM,AN=HN ∴∠MAG=∠G,∠NAD=∠H ∴∠AMN+∠ANM=∠MAG+∠G+∠NAD+∠H=2(∠G+∠H) 在△GAH中,∠G+∠H=180°-∠BAD=60° ∴∠AMN+∠ANM=∠MAG+∠G+∠NAD+∠H=2(∠G+∠H)=120°. 故答案为:120. 【分析】先通过作图确定出点M、N的位置,然后根据轴对称的性质得线段相等AM=GM,AN=HN,再由等边对等角得∠MAG=∠G,∠NAD=∠H,继而得∠AMN+∠ANM=2(∠G+∠H),然后在△GAH中利用三角形内角和定理得∠G+∠H=60°,从而得∠AMN+∠ANM。
10. 解:2∠C′=∠1+∠2.
理由:∵∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°,
∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°,
∴∠1+∠2=∠C+∠C′,
∵在△ABC中,C、C′关于DE对称,
∴∠C=∠C′,
∴2∠C′=∠1+∠2.
【分析】根据四边形的内角和和平角的定义可得∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°,∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°,则 ∠1+∠2=∠C+∠C′ ,再由对称的性质可得 ∠C=∠C′, 进而得出答案.www-2-1-cnjy-com
11. (1) (2) (3)12
解析:(1)过点B作点B关于对称轴的对称点D,连接AD和CD即可。 (2)将四边形ABCD的四个顶点分别向下平移5个单位长度,进行连线即可得到新的图形。 (3)将四边形的面积看作两个三角形的面积的和,即可得到答案。 【分析】(1)根据轴对称的性质即可得到D点,连接即可。 (2)根据平移的性质进行作图。 (3)将四边形的面积进行拆分,简便计算即可。【来源:21cnj*y.co*m】
三、真题演练
12. D
解析: D答案的图形是轴对称图形。 故答案为:D。
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可一一判断得出答案。21教育网
13. A
解析:1有两条对称轴;2有两条对称轴;3有四条对称轴;4不是对称图形。故答案为:A. 【分析】根据轴对称图形的特点确定对称轴即可。
14. D
解析:连接AD,
∵D点分别以AB、AC为对称轴,画出对称点E、F,
∴∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠DAC=180°-62°-51°=67°,
∴∠EAF=2∠BAC=134°,
故答案为:D.
【分析】连接AD,根据轴对称的性质得出∠EAB=∠BAD,∠FAC=∠CAD,根据三角形的内角和得出∠BAC=∠BAD+∠DAC=57°,根据角的和差及等量代换得出∠EAF=2∠BAC=134°。21教育名师原创作品
15. 解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
【分析】轴对称图形的定义:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。21*cnjy*com
一、基础巩固
1.如图所示的图案中,有2条对称轴的轴对称图形是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化.窗框一部分如图2所示,它是一个轴对称图形,其对称轴有(??? ) 21cnjy.com
A.?1条???????????????????????????????????????B.?2条???????????????????????????????????????C.?3条???????????????????????????????????????D.?4条
3.如图,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,则点C所表示的数
为________ 2·1·c·n·j·y
4.如图是一个风筝的图案,它是轴对称图形,量得∠B=20°,则∠E=________°.
5.如图,点P是∠AOB内一点,分别作出P点关于OA、OB的对称点E、F,连接EF交OA于M,交OB于N,EF=15,求△PMN的周长. 【来源:21·世纪·教育·网】
6.如图,△ABC和△A′B′C′关于直线m对称,
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样关系?
二、强化提升
7.如图6,C,E是直线l两侧的点,以点C为圆心,CE长为半径作圆弧交l于A,B两点;再分别以A,B为圆心,大于 AB的长为半径作圆弧,两弧交于点D,连接CA,CB,CD,下列结论不一定成立的是( ??) 21世纪教育网版权所有
A.?CD⊥l????????????B.?点A,B关于直线CD对称????????????C.?CD平分∠ACB????????????D.?点C,D关于直线l对称
8.如图所示的网格中各有不同的图案,不能通过平移得到的是(?? )
A.??????????????B.??????????????C.??????????????D.?
9.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM=________°. 21·世纪*教育网
10.在△ABC中,C、C′关于DE对称,判断∠1,∠2,∠C′的关系并证明.
11.如图,在边长为1个单位长度的小正方形组成的12×12的正方形网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,顶点都在格点上,其对称轴为直线AC。
(1)在图中标出点D,并画出该四边形的另两条边
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A‘B’C‘D’。
(3)直接写出四边形A‘B’C‘D’的面积
三、真题演练
12.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是(??? )
A.?当心吊物安全????????????????B.?当心触电安全 C.?当心滑跌安全???????????????????????D.?注意安全
13.下列图形:
其中是轴对称图形且有两条对称轴的是(???? )
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
14.如图,△ABC中,D点在BC上,将D点分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,求∠EAF的度数为何?(?? ) 【出处:21教育名师】
A.?113??????????????????????????????????????B.?124??????????????????????????????????????C.?129??????????????????????????????????????D.?134
15.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
答案解析部分
一、基础巩固
1. D
解析:A、B各有一条对称轴,故不正确;
C没有对称轴,故不正确;
D有两条对称轴,故正确;
故答案为:D. 【分析】如果两个图形关于某条直线对称,那么这条直线就是对称轴。由对称轴的定义可知:A、B各有一条对称轴;C没有对称轴;D有两条对称轴。2-1-c-n-j-y
2. B
解析:过窗框相对两边中点所在直线折叠,直线两旁的部分就能完全重合,故窗框的对称轴有两条。故答案为:B。
【分析】把一个平面图形沿着某一条直线折叠,直线两旁的部分能完全重合的几何图形就是轴对称图形;沿着对折的这条直线就是轴对称图形的对称轴,由于该图案过窗框相对两边中点所在直线折叠,直线两旁的部分就能完全重合,故窗框的对称轴有两条。
3. - -2
解析:∵ 数轴上A,B两点表示的数分别为-1和 , ∴AB=-(-1)=+1 点B关于点A的对称点为C, ∴AC=AB=+1 ∴点C所表示的数-1-(+1)= 故答案为:
【分析】根据点A、B的坐标求出AB的长,再根据轴对称的性质,由点B关于点A的对称点为C,可知AC=AB,就可求出AC的长,然后就可确定出点C所表示的数。
4. 20
解析:∵风筝的图案是轴对称图形,
∴∠E=∠B=20°.
故答案为:20.
【分析】根据轴对称图形的性质得∠E=∠B,即可求得.
5. 解:∵P点关于OA、OB的对称点分别为E、F,
∴PM=EM,PN=FN,
∴△PMN的周长=PM+MN+FN=ME+MN+FN=EF,
∵EF=15,
∴△PMN的周长=15.
【分析】根据轴对称的性质“ 如果两个图形关于某条直线对称,那么 对称轴是任何一对对应点所连 线段的垂直平分线”可得 PM=EM,PN=FN, 由图可得 △PMN的周长=PM+MN+FN=ME+MN+FN=EF。
6. (1)解:由图可知,对称点有A和A′,B和B′,C和C′ (2)解:连接AA′,直线m是线段AA′的垂直平分线; (3)解:延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或其延长线的交点在对称轴上.
【分析】(1)根据对称图形的性质和△ABC和△A′B′C′关于直线m对称,可得对称点; (2)根据“对称轴是两个对称点的连线的垂直平分线”可得答案; (3)根据轴对称的性质可直接得出结论.【版权所有:21教育】
二、强化提升
7. D
解析:连接AD,BD, ∵AC=BC,AD=BD,CD=CD ∴△ACD≌△BCD(SSS) ∴∠ACD=∠BCD, ∵AC=BC, ∴CD⊥AB,AO=BO, ∴CD垂直l, 点A,B关于直线CD对称 ,故A、B、C不符合题意; ∵CO与DO不一定相等, ∴C、D不一定关于直线l对称,故D符合题意; 故答案为:D. 【分析】根据“SSS”可证△ACD≌△BCD,可得∠ACD=∠BCD,利用等腰三角形三线合一的性质可得CD⊥AB,AO=BO,据此判断A、B、C;由于CO与DO不一定相等,据此可判断D.
8. C
解析: A、可以通过平移得到,不符合题意;
B、可以通过平移得到,不符合题意;
C、先利用轴对称,再通过平移得到,符合题意;
D、可以通过平移得到,不符合题意.
故答案为:C
【分析】平移是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动, 简称平移。根据定义即可判断求解。www.21-cn-jy.com
9. 120
解析:作点A关于BC的对称点G,作点A关于DC的对称点H,连接HG,分别交BC、DC于点M、N。连接AM、AN。则AM=GM,AN=HN ∴∠MAG=∠G,∠NAD=∠H ∴∠AMN+∠ANM=∠MAG+∠G+∠NAD+∠H=2(∠G+∠H) 在△GAH中,∠G+∠H=180°-∠BAD=60° ∴∠AMN+∠ANM=∠MAG+∠G+∠NAD+∠H=2(∠G+∠H)=120°. 故答案为:120. 【分析】先通过作图确定出点M、N的位置,然后根据轴对称的性质得线段相等AM=GM,AN=HN,再由等边对等角得∠MAG=∠G,∠NAD=∠H,继而得∠AMN+∠ANM=2(∠G+∠H),然后在△GAH中利用三角形内角和定理得∠G+∠H=60°,从而得∠AMN+∠ANM。
10. 解:2∠C′=∠1+∠2.
理由:∵∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°,
∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°,
∴∠1+∠2=∠C+∠C′,
∵在△ABC中,C、C′关于DE对称,
∴∠C=∠C′,
∴2∠C′=∠1+∠2.
【分析】根据四边形的内角和和平角的定义可得∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°,∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°,则 ∠1+∠2=∠C+∠C′ ,再由对称的性质可得 ∠C=∠C′, 进而得出答案.www-2-1-cnjy-com
11. (1) (2) (3)12
解析:(1)过点B作点B关于对称轴的对称点D,连接AD和CD即可。 (2)将四边形ABCD的四个顶点分别向下平移5个单位长度,进行连线即可得到新的图形。 (3)将四边形的面积看作两个三角形的面积的和,即可得到答案。 【分析】(1)根据轴对称的性质即可得到D点,连接即可。 (2)根据平移的性质进行作图。 (3)将四边形的面积进行拆分,简便计算即可。【来源:21cnj*y.co*m】
三、真题演练
12. D
解析: D答案的图形是轴对称图形。 故答案为:D。
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可一一判断得出答案。21教育网
13. A
解析:1有两条对称轴;2有两条对称轴;3有四条对称轴;4不是对称图形。故答案为:A. 【分析】根据轴对称图形的特点确定对称轴即可。
14. D
解析:连接AD,
∵D点分别以AB、AC为对称轴,画出对称点E、F,
∴∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠DAC=180°-62°-51°=67°,
∴∠EAF=2∠BAC=134°,
故答案为:D.
【分析】连接AD,根据轴对称的性质得出∠EAB=∠BAD,∠FAC=∠CAD,根据三角形的内角和得出∠BAC=∠BAD+∠DAC=57°,根据角的和差及等量代换得出∠EAF=2∠BAC=134°。21教育名师原创作品
15. 解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
【分析】轴对称图形的定义:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。21*cnjy*com
