12.3 角的平分线的性质 同步练习(解析版)
文档属性
| 名称 | 12.3 角的平分线的性质 同步练习(解析版) | 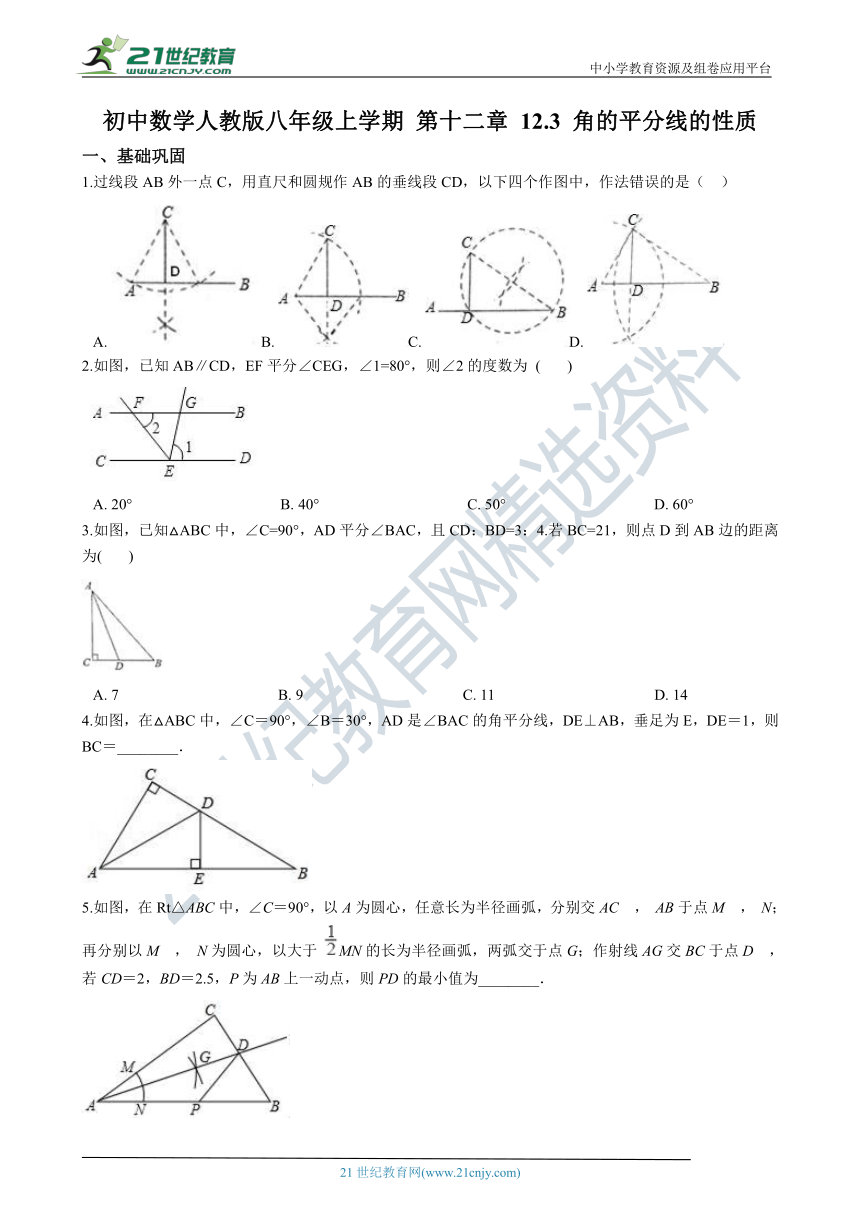 | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 09:16:39 | ||
图片预览





文档简介
初中数学人教版八年级上学期 第十二章 12.3 角的平分线的性质
一、基础巩固
1.过线段AB外一点C,用直尺和圆规作AB的垂线段CD,以下四个作图中,作法错误的是( ??)
A.?B.?C.?D.?
2.如图,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为 (??? )
A.?20°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为(??? ) 21世纪教育网版权所有
A.?7??????????????????????????????????????????B.?9??????????????????????????????????????????C.?11??????????????????????????????????????????D.?14
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=________. 21cnjy.com
5.如图,在Rt△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC , AB于点M , N;再分别以M , N为圆心,以大于 MN的长为半径画弧,两弧交于点G;作射线AG交BC于点D , 若CD=2,BD=2.5,P为AB上一动点,则PD的最小值为________. 2·1·c·n·j·y
6.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为________. 【版权所有:21教育】
7.尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.2-1-c-n-j-y
由步骤①,得____________________
由步骤②,得____________________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由____________________.
??????????
8.如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.
求证:EB=FC.
9.如图AB=AC,BD=CD,DE⊥BA,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
二、强化提升
10.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是( ) 21*cnjy*com
A.?6cm????????????????????????????????????B.?7cm????????????????????????????????????C.?8cm????????????????????????????????????D.?9 cm
11.如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为(?? )
A.?α??????????????????????????????????B.???????????????????????????????????C.?90﹣α??????????????????????????????????D.?90﹣ α
12.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④若AC=4BE,则S△ABC=8S△BDE其中正确的有( ??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有(?? )
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
14.如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=28,则DE=________
15.如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是________; 【来源:21cnj*y.co*m】
16.如图,DE∥BC,DF、BE分别平分∠ADE、∠ABC,求证:∠FDE=∠DEB。
17.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,
求证:
(1)DF∥BC;
(2)FG=FE.
三、真题演练
18.如图.在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为(??? )
A.?40°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
19.如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中符合题意的个数为(??? ). 21教育网
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
20.己知:∠AOB.
? 求作:∠A'O'B',使得A'O'B'=∠AOB.
? 作法:
? ①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
? ②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
? ③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';
? ④过点D'画射线O'B',则∠A'O'B'=∠AOB.
? 根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出∠A'O'B'? (请保留作图痕迹).
(2)完成下面证明∠A'O'B'=∠AOB的过程(注:括号里填写推理的依据).
? 证明:由作法可知O'C'=OC,O'D'=OD,D'C'=________?,
? ∴△C'O'D'≌△COD________
? ∴∠A'O'B'= ∠AOB.________
答案解析部分
一、基础巩固
1. B
解析:A、根据过直线外一点作已知直线的尺规作图可知此选项不符合题意;
B、无法证明CD是AB上的垂线,符合题意.
C、根据直径所对的圆周角是直角的方法可知,CD是AB上的垂线段,不符合题意;
D、根据相交两圆的公共弦的性质可知,CD是AB上的垂线段,不符合题意;
故答案为:B.
【分析】根据过直线外一点作已知直线垂线的方法直接判断A;根据直径所对的圆周角是直角,据此判断C;根据相交两圆的公共弦的性质,可得CD⊥AB,据此判断D,从而求出答案.
2. C
解析:∵∠1=80°,∴∠CEG=100°,又∵ EF平分∠CEG, ∴∠CEF=50°,∵AB∥CD,故∠2=∠CEF=50°. 故答案为:C 【分析】先根据平角的定义和角平分线的定义求得∠CEF的大小,再由平行线的性质即可求出∠2的大小。
3. B
解析:∵CD:BD=3:4.
设CD=3x,则BD=4x,
∴BC=CD+BD=7x,
∵BC=21,
∴7x=21,
∴x=3,
∴CD=9,
过点D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,
∴DE=CD=9,
∴点D到AB边的距离是9,
故答案为:B. 【分析】由题意易求得CD的长,过点D作DE⊥AB于E,根据角平分线上的点到角两边的距离相等即可求得点D到AB边的距离=CD的长。21·cn·jy·com
4. 3
解析:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故答案为:3.
【分析】由角平分线的性质可知CD=DE=1;∠B=30°,DE⊥AB,根据30°所对的直角边等于斜边的一半,即DB=2DE=2,即可求得BC的长。【来源:21·世纪·教育·网】
5. 2
解析:由作法得AD平分∠BAC ,
∴点D到AB的距离等于DC=2,
∴PD的最小值为2.
故答案为:2. 【分析】根据题目可知该作法是∠BAC的角平分线的作法,所以AD平分∠BAC。P是AB上的动点,只有当PD⊥AB时,PD的值最短,则题目转化为求D到AB的距离。根据角平分线的点到角两边距离相等这一性质可推出PD最小值就是CD的值。21*cnjy*com
6. 4
解析:∵BC=10cm,BD:DC=3:2,
∴BD=6cm,CD=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
【分析】因为点D到AB的距离是点D到AB的垂线段的长度,根据角平分线上的点到角两边的距离相等可知CD与点D到AB的距离相等,结合已知可求得CD的长。【出处:21教育名师】
7. PA=PB ;AB=BA' ;根据线段相等,即可证明三角形全等,证明对称 21教育名师原创作品
【分析】根据尺规作图的步骤,写出内容即可,根据线段相等求得点的对称点。
8. 证明:∵AD平分角BAC? DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,
?
∴Rt△BDE≌Rt△CDF,
∴DE=DF.
【分析】根据角平分线上的点到这个角两边的距离相等可得DE=DF, 利用HL判Rt△BDE≌Rt△CDF, 由全等三角形的对应边相等即可证明EB=FC.
9. 证明:在△ABD和△ACD中, ,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵DE⊥BA,DF⊥AC,
∴DE=DF.
【分析】利用SSS证明△ABD≌△ACD,再根据全等三角形的性质,可证得∠BAD=∠CAD,然后根据角平分线的性质,可证得结论。
二、强化提升
10. A
解析:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于E,∴CD=DE.
又∵AD=AD,
∴Rt△ACD≌Rt△AED,∴AC=AE.
又∵AC=BC,
∴△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=6
故答案为:A 【分析】 由角平分线上的点到角两边的距离相等可得CD=DE,然后用HL定理可证
Rt△ACD≌Rt△AED,根据全等三角形的对应边相等可得AC=AE,结合题意可得△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB可求解。
11. C
解析:如图,过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,
∵∠ABD=52°,∠ABC=116°,
∴∠DBC=∠CBE=64°,
∴BC平分∠DBE,
∴CE=CF,
又∵AC平分∠BAD,
∴CE=CG,
∴CF=CG,
又∵CG⊥AD,CF⊥DB,
∴CD平分∠BDG,
∵∠CBE是△ABC的外角,∠DBE是△ABD的外角,
∴∠ACB=∠CBE﹣∠CAB= (∠DBE﹣∠DAB)= ∠ADB,
∴∠ADB=2∠ACB=2α°,
∴∠BDG=180°﹣2α°,
∴∠BDC= ∠BDG=90°﹣α°,
故答案为:C.
【分析】过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,根据角平分线的判定可得到CD平分∠BDG,再根据三角形外角性质,即可得出∠BDC的度数.
12. B
解析:①∵ AD平分∠BAC ,DE⊥AB , ∠C=90°, ∴DC=DE,∠DAE=∠DAC,∠C=∠DEA=90°, 在Rt△ADE和Rt△ADC中, ∵, ∴Rt△ADE≌Rt△ADC(HL), ∴∠ADE=∠ADC,AE=AC, ∴ AD平分∠CDE , 故①正确; ② ∵∠C=90°, ∴∠B+∠BAC=90°, ∵ DE⊥AB , ∴∠DEB=90°, ∴∠B+∠BDE=90°, ∴∠BAC=∠BDE, 故②正确; ③无法证明DE平分∠ADB, 故③错误; ④由①知AE=AC, ∵AB=AE+BE=AC+BE,AC=4BE, ∴AB=5BE, ∴S△ADB=·AB·DE=·5BE·DE=5S△BDE , S△ADC=·AC·DC=·4BE·DE=4S△BDE , ∴S△ABC=S△ADB+S△ADC , =5S△BDE+4S△BDE , =9S△BDE.故④错误; 综上所述:正确的有①②. 故答案为:B. 【分析】①根据角平分线的性质定理可知 DC=DE,由全等三角形的判定HL得Rt△ADE≌Rt△ADC,由全等三角形的性质可得∠ADE=∠ADC,即AD平分 ∠CDE ,从而可得①正确; ② 根据同角的余角相等即可得②正确; ③无法证明DE平分∠ADB, 故③错误; ④由①知AE=AC,结合题意可得AB=5BE,根据线段之间的关系以及三角形的面积公式即可得S△ABC=9S△BDE , 故④错误;
13. A
解析:①正确,因为角平分线上的点到两边的距离相等知;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的补角相等,所以∠BDE=∠BAC;
④正确,因为由△ADC≌△ADE可知,∠ADC=∠ADE,所以AD平分∠CDE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△ABD:S△ACD=AB:AC.
所以正确的有五个,故答案为:A.
【分析】根据角平分线上的点到这个角两边的距离相等可知①正确;根据HL可判定△ADC≌△ADE,由全等三角形的对应边相等可得AC=AE,进而可得AC+BE=AB; 故②正确;根据同角的余角相等可知③正确;由△ADC≌△ADE的对应角相等可得∠BDE=∠BAC; 故④正确;根据 S△ABD与S△ACD的边AB、AC 上的高相等可得S△ABD:S△ACD=AB:AC ;故⑤正确;由此作出判断即可.
14. 4
解析:∵ BD平分∠ABC,DE⊥AB于E,DF⊥BC于F ∴DE=DF ∵ S△ABC=S△ABD+S△ADC=28 ∴, 即 解之:DE=4 故答案为:4
【分析】利用角平分线的性质,易证DE=DF,再根据S△ABC=S△ABD+S△ADC=28 ,建立关于DE的方程,解方程求出DE的长。
15. 11
解析:如图:作PE⊥OB,PG⊥OA,PF⊥MN,连结OP, ∵PM、PN分别平分∠AMN,∠BNM, ∴PF=PG=PE, ∵S△PMN=·MN·PF=2,MN=2, ∴PF=PG=PE=2, 由题易得: △GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP, ∴GM=GF,FN=NE,OG=OE, ∴S△OPG=S△OPE=×(2+2+7)=, 即S△OPG=·OG·PG=, ∴OG=, ∴C△MON=OM+ON+MN, =OM+ON+MF+FN, =OM+ON+MG+NE, =OG+OE, =2OG, =2×, =11. 故答案为:11.
【分析】作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,根据角平分线的性质定理得PF=PG=PE,再由三角形面积公式得PF=PG=PE=2,据条件易得:△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,由全等三角形性质得GM=GF,FN=NE,OG=OE,S△OPG=·OG·PG=得OG=, 由三角形周长和等量代换可得答案.
16. 证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ∠ADE,∠ABE= ∠ABC,
∴∠ADF=∠ABE
∴DF∥BE,
∴∠FDE=∠DEB
【分析】根据直线平行的性质,得到∠ADE=∠ABC,由角的平分线定理,即可证明∠ADF=∠ABE,根据直线平行的判定定理得到DF∥BE,根据直线平行的性质作答即可。www.21-cn-jy.com
17. (1)证明:∵AF平分∠CAB,
∴∠CAF=∠DAF.
在△ACF和△ADF中,
∵ ,
∴△ACF≌△ADF(SAS).
∴∠ACF=∠ADF.
∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠CAE=90°,∠CAE+∠B=90°,
∴∠ACF=∠B,
∴∠ADF=∠B.
∴DF∥BC. (2)证明:∵DF∥BC,BC⊥AC,
∴FG⊥AC.
∵FE⊥AB,
又AF平分∠CAB,
∴FG=FE.
【分析】(1)根据题中条件利用“SAS”判定 △ACF≌△ADF ,由全等三角形对应角相等可得 ∠ACF=∠ADF ,由同角的余角相等得 ∠ACF=∠B ,从而可证 ∠ADF=∠B ,最后根据同位角相等,两直线平行可证 DF∥BC . (2)结合(1)中结论,根据角平分线上的点到角两边的距离相等可证 FG=FE .
三、真题演练
18. C
解析:由作法可知: CG⊥AB ∵AC=BC, ∴CG平分∠ACB,∠A=∠B=40° ∴∠ACB=180°-40°-40°=100° ∴∠BCG=∠ACB=×100°=50° 故答案为:C 【分析】利用等腰三角形的性质和作图可知CG⊥AB,CG平分∠ACB,∠A=∠B,再利用三角形内角和定理求出∠ACB,然后求出∠BCG的度数。21·世纪*教育网
19. B
解析:
解:∵ ,
∴ ,
即 ,
在 和 中, ,
∴ ,
∴ ,①符合题意;
∴ ,
由三角形的外角性质得:
∴ °,②符合题意;
作 于 , 于 ,如图所示:
则 °,
在 和 中, ,
∴ ,
∴ ,
∴ 平分 ,④符合题意;
正确的个数有3个;故答案为:B. 【分析】根据“SAS”可证△AOC≌△BOD,利用全等三角形的性质,可得∠OCA=∠ODB,AC=BD,据此判断①;根据三角形内角和定理,可得∠OAC=∠OBD,根据三角形的外角性质,可得∠AMB=∠AOB=40°,据此判断②;作 于 , 于 ,根据“AAS”可证△OCG≌△ODH,即可OG=OH,利用到角两边距离相等的点在角的平分线上,可得MO平分∠BMC,据此判断③④;
20. (1)解:解:如图所示,∠A'O'B'即为所求;
(2)DC;SSS;全等三角形的对应角相等
解析:证明:由作法可知O'C'=OC,O'D'=OD,D'C'=DC,
? ∴△C'O'D' ≌△COD(SSS)
? ∴∠A'O'B'=∠AOB.(全等三角形的对应角相等)
? 故答案为:DC,SSS,伞等三角形的对应角相等。 【分析】(1)根据题干提供的方法用尺规作出∠ A'O'B'? 即可; (2)根据作图过程可知: O'C'=OC,O'D'=OD,D'C'= DC,然后根据SSS判断出 △C'O'D'≌△COD ,根据全等三角形对应角相等即可得出 ∠A'O'B'= ∠AOB 。www-2-1-cnjy-com
一、基础巩固
1.过线段AB外一点C,用直尺和圆规作AB的垂线段CD,以下四个作图中,作法错误的是( ??)
A.?B.?C.?D.?
2.如图,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为 (??? )
A.?20°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为(??? ) 21世纪教育网版权所有
A.?7??????????????????????????????????????????B.?9??????????????????????????????????????????C.?11??????????????????????????????????????????D.?14
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=________. 21cnjy.com
5.如图,在Rt△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC , AB于点M , N;再分别以M , N为圆心,以大于 MN的长为半径画弧,两弧交于点G;作射线AG交BC于点D , 若CD=2,BD=2.5,P为AB上一动点,则PD的最小值为________. 2·1·c·n·j·y
6.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为________. 【版权所有:21教育】
7.尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.2-1-c-n-j-y
由步骤①,得____________________
由步骤②,得____________________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由____________________.
??????????
8.如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.
求证:EB=FC.
9.如图AB=AC,BD=CD,DE⊥BA,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
二、强化提升
10.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是( ) 21*cnjy*com
A.?6cm????????????????????????????????????B.?7cm????????????????????????????????????C.?8cm????????????????????????????????????D.?9 cm
11.如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为(?? )
A.?α??????????????????????????????????B.???????????????????????????????????C.?90﹣α??????????????????????????????????D.?90﹣ α
12.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④若AC=4BE,则S△ABC=8S△BDE其中正确的有( ??)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有(?? )
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
14.如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=28,则DE=________
15.如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是________; 【来源:21cnj*y.co*m】
16.如图,DE∥BC,DF、BE分别平分∠ADE、∠ABC,求证:∠FDE=∠DEB。
17.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,
求证:
(1)DF∥BC;
(2)FG=FE.
三、真题演练
18.如图.在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为(??? )
A.?40°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
19.如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中符合题意的个数为(??? ). 21教育网
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
20.己知:∠AOB.
? 求作:∠A'O'B',使得A'O'B'=∠AOB.
? 作法:
? ①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
? ②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
? ③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';
? ④过点D'画射线O'B',则∠A'O'B'=∠AOB.
? 根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出∠A'O'B'? (请保留作图痕迹).
(2)完成下面证明∠A'O'B'=∠AOB的过程(注:括号里填写推理的依据).
? 证明:由作法可知O'C'=OC,O'D'=OD,D'C'=________?,
? ∴△C'O'D'≌△COD________
? ∴∠A'O'B'= ∠AOB.________
答案解析部分
一、基础巩固
1. B
解析:A、根据过直线外一点作已知直线的尺规作图可知此选项不符合题意;
B、无法证明CD是AB上的垂线,符合题意.
C、根据直径所对的圆周角是直角的方法可知,CD是AB上的垂线段,不符合题意;
D、根据相交两圆的公共弦的性质可知,CD是AB上的垂线段,不符合题意;
故答案为:B.
【分析】根据过直线外一点作已知直线垂线的方法直接判断A;根据直径所对的圆周角是直角,据此判断C;根据相交两圆的公共弦的性质,可得CD⊥AB,据此判断D,从而求出答案.
2. C
解析:∵∠1=80°,∴∠CEG=100°,又∵ EF平分∠CEG, ∴∠CEF=50°,∵AB∥CD,故∠2=∠CEF=50°. 故答案为:C 【分析】先根据平角的定义和角平分线的定义求得∠CEF的大小,再由平行线的性质即可求出∠2的大小。
3. B
解析:∵CD:BD=3:4.
设CD=3x,则BD=4x,
∴BC=CD+BD=7x,
∵BC=21,
∴7x=21,
∴x=3,
∴CD=9,
过点D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,
∴DE=CD=9,
∴点D到AB边的距离是9,
故答案为:B. 【分析】由题意易求得CD的长,过点D作DE⊥AB于E,根据角平分线上的点到角两边的距离相等即可求得点D到AB边的距离=CD的长。21·cn·jy·com
4. 3
解析:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故答案为:3.
【分析】由角平分线的性质可知CD=DE=1;∠B=30°,DE⊥AB,根据30°所对的直角边等于斜边的一半,即DB=2DE=2,即可求得BC的长。【来源:21·世纪·教育·网】
5. 2
解析:由作法得AD平分∠BAC ,
∴点D到AB的距离等于DC=2,
∴PD的最小值为2.
故答案为:2. 【分析】根据题目可知该作法是∠BAC的角平分线的作法,所以AD平分∠BAC。P是AB上的动点,只有当PD⊥AB时,PD的值最短,则题目转化为求D到AB的距离。根据角平分线的点到角两边距离相等这一性质可推出PD最小值就是CD的值。21*cnjy*com
6. 4
解析:∵BC=10cm,BD:DC=3:2,
∴BD=6cm,CD=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
【分析】因为点D到AB的距离是点D到AB的垂线段的长度,根据角平分线上的点到角两边的距离相等可知CD与点D到AB的距离相等,结合已知可求得CD的长。【出处:21教育名师】
7. PA=PB ;AB=BA' ;根据线段相等,即可证明三角形全等,证明对称 21教育名师原创作品
【分析】根据尺规作图的步骤,写出内容即可,根据线段相等求得点的对称点。
8. 证明:∵AD平分角BAC? DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,
?
∴Rt△BDE≌Rt△CDF,
∴DE=DF.
【分析】根据角平分线上的点到这个角两边的距离相等可得DE=DF, 利用HL判Rt△BDE≌Rt△CDF, 由全等三角形的对应边相等即可证明EB=FC.
9. 证明:在△ABD和△ACD中, ,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵DE⊥BA,DF⊥AC,
∴DE=DF.
【分析】利用SSS证明△ABD≌△ACD,再根据全等三角形的性质,可证得∠BAD=∠CAD,然后根据角平分线的性质,可证得结论。
二、强化提升
10. A
解析:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于E,∴CD=DE.
又∵AD=AD,
∴Rt△ACD≌Rt△AED,∴AC=AE.
又∵AC=BC,
∴△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=6
故答案为:A 【分析】 由角平分线上的点到角两边的距离相等可得CD=DE,然后用HL定理可证
Rt△ACD≌Rt△AED,根据全等三角形的对应边相等可得AC=AE,结合题意可得△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB可求解。
11. C
解析:如图,过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,
∵∠ABD=52°,∠ABC=116°,
∴∠DBC=∠CBE=64°,
∴BC平分∠DBE,
∴CE=CF,
又∵AC平分∠BAD,
∴CE=CG,
∴CF=CG,
又∵CG⊥AD,CF⊥DB,
∴CD平分∠BDG,
∵∠CBE是△ABC的外角,∠DBE是△ABD的外角,
∴∠ACB=∠CBE﹣∠CAB= (∠DBE﹣∠DAB)= ∠ADB,
∴∠ADB=2∠ACB=2α°,
∴∠BDG=180°﹣2α°,
∴∠BDC= ∠BDG=90°﹣α°,
故答案为:C.
【分析】过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,根据角平分线的判定可得到CD平分∠BDG,再根据三角形外角性质,即可得出∠BDC的度数.
12. B
解析:①∵ AD平分∠BAC ,DE⊥AB , ∠C=90°, ∴DC=DE,∠DAE=∠DAC,∠C=∠DEA=90°, 在Rt△ADE和Rt△ADC中, ∵, ∴Rt△ADE≌Rt△ADC(HL), ∴∠ADE=∠ADC,AE=AC, ∴ AD平分∠CDE , 故①正确; ② ∵∠C=90°, ∴∠B+∠BAC=90°, ∵ DE⊥AB , ∴∠DEB=90°, ∴∠B+∠BDE=90°, ∴∠BAC=∠BDE, 故②正确; ③无法证明DE平分∠ADB, 故③错误; ④由①知AE=AC, ∵AB=AE+BE=AC+BE,AC=4BE, ∴AB=5BE, ∴S△ADB=·AB·DE=·5BE·DE=5S△BDE , S△ADC=·AC·DC=·4BE·DE=4S△BDE , ∴S△ABC=S△ADB+S△ADC , =5S△BDE+4S△BDE , =9S△BDE.故④错误; 综上所述:正确的有①②. 故答案为:B. 【分析】①根据角平分线的性质定理可知 DC=DE,由全等三角形的判定HL得Rt△ADE≌Rt△ADC,由全等三角形的性质可得∠ADE=∠ADC,即AD平分 ∠CDE ,从而可得①正确; ② 根据同角的余角相等即可得②正确; ③无法证明DE平分∠ADB, 故③错误; ④由①知AE=AC,结合题意可得AB=5BE,根据线段之间的关系以及三角形的面积公式即可得S△ABC=9S△BDE , 故④错误;
13. A
解析:①正确,因为角平分线上的点到两边的距离相等知;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的补角相等,所以∠BDE=∠BAC;
④正确,因为由△ADC≌△ADE可知,∠ADC=∠ADE,所以AD平分∠CDE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△ABD:S△ACD=AB:AC.
所以正确的有五个,故答案为:A.
【分析】根据角平分线上的点到这个角两边的距离相等可知①正确;根据HL可判定△ADC≌△ADE,由全等三角形的对应边相等可得AC=AE,进而可得AC+BE=AB; 故②正确;根据同角的余角相等可知③正确;由△ADC≌△ADE的对应角相等可得∠BDE=∠BAC; 故④正确;根据 S△ABD与S△ACD的边AB、AC 上的高相等可得S△ABD:S△ACD=AB:AC ;故⑤正确;由此作出判断即可.
14. 4
解析:∵ BD平分∠ABC,DE⊥AB于E,DF⊥BC于F ∴DE=DF ∵ S△ABC=S△ABD+S△ADC=28 ∴, 即 解之:DE=4 故答案为:4
【分析】利用角平分线的性质,易证DE=DF,再根据S△ABC=S△ABD+S△ADC=28 ,建立关于DE的方程,解方程求出DE的长。
15. 11
解析:如图:作PE⊥OB,PG⊥OA,PF⊥MN,连结OP, ∵PM、PN分别平分∠AMN,∠BNM, ∴PF=PG=PE, ∵S△PMN=·MN·PF=2,MN=2, ∴PF=PG=PE=2, 由题易得: △GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP, ∴GM=GF,FN=NE,OG=OE, ∴S△OPG=S△OPE=×(2+2+7)=, 即S△OPG=·OG·PG=, ∴OG=, ∴C△MON=OM+ON+MN, =OM+ON+MF+FN, =OM+ON+MG+NE, =OG+OE, =2OG, =2×, =11. 故答案为:11.
【分析】作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,根据角平分线的性质定理得PF=PG=PE,再由三角形面积公式得PF=PG=PE=2,据条件易得:△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,由全等三角形性质得GM=GF,FN=NE,OG=OE,S△OPG=·OG·PG=得OG=, 由三角形周长和等量代换可得答案.
16. 证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ∠ADE,∠ABE= ∠ABC,
∴∠ADF=∠ABE
∴DF∥BE,
∴∠FDE=∠DEB
【分析】根据直线平行的性质,得到∠ADE=∠ABC,由角的平分线定理,即可证明∠ADF=∠ABE,根据直线平行的判定定理得到DF∥BE,根据直线平行的性质作答即可。www.21-cn-jy.com
17. (1)证明:∵AF平分∠CAB,
∴∠CAF=∠DAF.
在△ACF和△ADF中,
∵ ,
∴△ACF≌△ADF(SAS).
∴∠ACF=∠ADF.
∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠CAE=90°,∠CAE+∠B=90°,
∴∠ACF=∠B,
∴∠ADF=∠B.
∴DF∥BC. (2)证明:∵DF∥BC,BC⊥AC,
∴FG⊥AC.
∵FE⊥AB,
又AF平分∠CAB,
∴FG=FE.
【分析】(1)根据题中条件利用“SAS”判定 △ACF≌△ADF ,由全等三角形对应角相等可得 ∠ACF=∠ADF ,由同角的余角相等得 ∠ACF=∠B ,从而可证 ∠ADF=∠B ,最后根据同位角相等,两直线平行可证 DF∥BC . (2)结合(1)中结论,根据角平分线上的点到角两边的距离相等可证 FG=FE .
三、真题演练
18. C
解析:由作法可知: CG⊥AB ∵AC=BC, ∴CG平分∠ACB,∠A=∠B=40° ∴∠ACB=180°-40°-40°=100° ∴∠BCG=∠ACB=×100°=50° 故答案为:C 【分析】利用等腰三角形的性质和作图可知CG⊥AB,CG平分∠ACB,∠A=∠B,再利用三角形内角和定理求出∠ACB,然后求出∠BCG的度数。21·世纪*教育网
19. B
解析:
解:∵ ,
∴ ,
即 ,
在 和 中, ,
∴ ,
∴ ,①符合题意;
∴ ,
由三角形的外角性质得:
∴ °,②符合题意;
作 于 , 于 ,如图所示:
则 °,
在 和 中, ,
∴ ,
∴ ,
∴ 平分 ,④符合题意;
正确的个数有3个;故答案为:B. 【分析】根据“SAS”可证△AOC≌△BOD,利用全等三角形的性质,可得∠OCA=∠ODB,AC=BD,据此判断①;根据三角形内角和定理,可得∠OAC=∠OBD,根据三角形的外角性质,可得∠AMB=∠AOB=40°,据此判断②;作 于 , 于 ,根据“AAS”可证△OCG≌△ODH,即可OG=OH,利用到角两边距离相等的点在角的平分线上,可得MO平分∠BMC,据此判断③④;
20. (1)解:解:如图所示,∠A'O'B'即为所求;
(2)DC;SSS;全等三角形的对应角相等
解析:证明:由作法可知O'C'=OC,O'D'=OD,D'C'=DC,
? ∴△C'O'D' ≌△COD(SSS)
? ∴∠A'O'B'=∠AOB.(全等三角形的对应角相等)
? 故答案为:DC,SSS,伞等三角形的对应角相等。 【分析】(1)根据题干提供的方法用尺规作出∠ A'O'B'? 即可; (2)根据作图过程可知: O'C'=OC,O'D'=OD,D'C'= DC,然后根据SSS判断出 △C'O'D'≌△COD ,根据全等三角形对应角相等即可得出 ∠A'O'B'= ∠AOB 。www-2-1-cnjy-com
