22.1.1 二次函数 同步练习(解析版)
文档属性
| 名称 | 22.1.1 二次函数 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 00:00:00 | ||
图片预览


文档简介
初中数学人教版九年级上学期 第二十二章 22.1.1 二次函数
一、基础巩固
1.函数 ( 是常数)是二次函数的条件是(?? )
A.?????????????????B.?????????????????C.?????????????????D.?
2.二次函数 的一次项系数是( ??)
A.?1??????????????????????????????????????????B.?-1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?-2
3.下列各式中,y是x的二次函数的是(??? )
A.?xy+x2=2???????????????????????????B.?x2﹣2y+2=0???????????????????????????C.?y= ???????????????? ???????????D.?y2﹣x=0
4.某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为(?? ) www.21-cn-jy.com
A.?y=100(1﹣x)2???????????????????????????????????????????????B.?y=100(1+x)2 C.?y= ??????????????????????????????????????????????????????????D.?y=100+100(1+x)+100(1+x)2
5.若 是关于自变量x的二次函数,则 ________.
6.已知函数y=(m+2)xm(m+1)是二次函数,则m=________.
二、强化提升
7.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(?? ) 21cnjy.com
A.?y=?????????????????????????????B.??? y= ?????????????????????????????C.??? y= ?????????????????????????????D.?y=
8.喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为(?? ) www-2-1-cnjy-com
A.?y=﹣10x2+100x+2000??????????????????????????????????????B.?y=10x2+100x+2000 C.?y=﹣10x2+200x???????????????????????????????????????? ??????D.?y=﹣10x2﹣100x+200021*cnjy*com
9.已知 是x的二次函数,求出它的解析式.
10.如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,求y与x之间的函数表达式. 【出处:21教育名师】
11.已知函数y=﹣(m+2)xm2﹣2(m为常数),求当m为何值时:
(1)y是x的一次函数?
(2)y是x的二次函数?并求出此时纵坐标为﹣8的点的坐标.
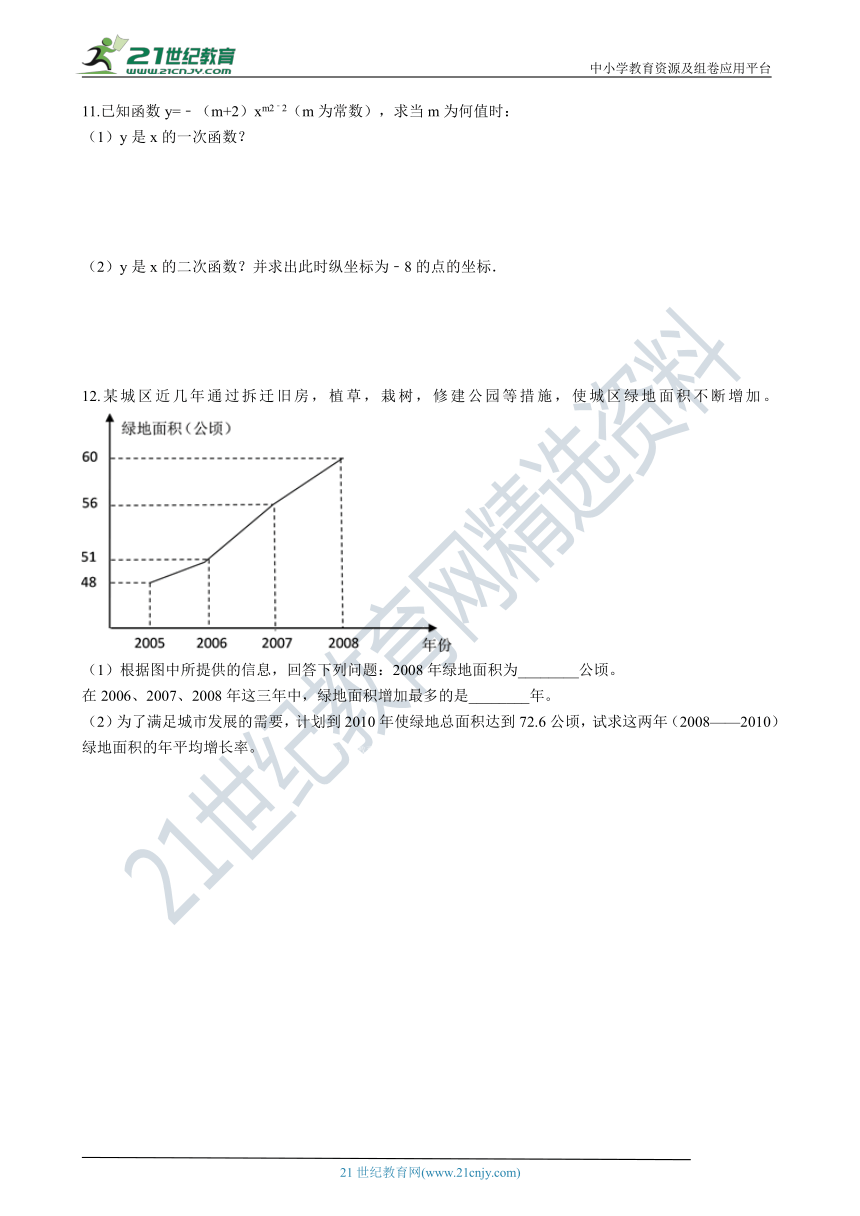
12.某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加。
(1)根据图中所提供的信息,回答下列问题:2008年绿地面积为________公顷。
在2006、2007、2008年这三年中,绿地面积增加最多的是________年。
(2)为了满足城市发展的需要,计划到2010年使绿地总面积达到72.6公顷,试求这两年(2008——2010)绿地面积的年平均增长率。 【版权所有:21教育】
答案解析部分
一、基础巩固
1.D
解析:根据二次函数定义中对常数a,b,c的要求,只要a≠0,b,c可以是任意实数,故答案为:D.21*cnjy*com
【分析】根据二次函数定义中对常数a,b,c的要求,只要a≠0即可。
2. D
解析:∵原二次函数可化为 ?∴其一次项系数是?2.故答案为::D.
【分析】将原函数整理成一般形式,即可得出其一次项的系数。
3.B
解析:A、整理为y= + ,不是二次函数,故不符合题意;
B、x2﹣2y+2=0变形,得y= x2+1,是二次函数,故符合题意;
C、分母中含自变量,不是二次函数,故不符合题意;
D、y的指数是2,不是函数,故不符合题意.
故答案为:B.
【分析】将A中的关系式转化为y是x的函数,即可判断;将B变形,转化为y是x的函数,利用二次函数的定义可作出判断;C中含自变量的式子是分式,不是二次函数;D中y的次数是2次,y不是x的函数,即可得出答案。2·1·c·n·j·y
4. B
解析:根据题意,由“2017年的产量=2015年的产量×(1+年平均增长率)2”得:y关于x的函数关系式为y=100(1+x)2. 故答案为:B. 【分析】根据“2017年的产量=2015年的产量×(1+年平均增长率)2”列出等量即可.
5. 2
解析:根据二次函数的定义,得:m2﹣2=2,解得:m=2或m=﹣2.
又∵m+2≠0,∴m≠﹣2,∴当m=2时,这个函数是二次函数.
故答案为:2.
【分析】根据二次函数的定义:自变量的最高指数为2,且二次项的系数不能为0,从而列出混合组,求解即可。【来源:21cnj*y.co*m】
6.1
解析:∵函数y=(m+2)xm(m+1)是二次函数, ∴ ?,
解得m=1.故答案为:1. 【分析】由于二次函数中自变量的最高指数只能为2,二次项的系数不能为0,从而列出混合组,求解即可。
二、强化提升
7. C
解析:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2 , 即(3a)2+(4a)2=x2 ,
解得:a= ,
∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF
= ×(a+4a)×4a
=10a2= x2 .
故答案为:C.
【分析】作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,利用AAS判定△ABC和△ADE全等,然后利用全等三角形的性质得出BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,利用勾股定理求出a与x的关系,分别用含x的代数式表示出DE、DF、AC,求出梯形AEDC的面积即为四边形ABCD的面积。【来源:21·世纪·教育·网】?
8. A
解析:设每件商品的售价上涨x元(x为正整数),
则每件商品的利润为:(60﹣50+x)元,
总销量为:(200﹣10x)件,
商品利润为:
y=(60﹣50+x)(200﹣10x),
=(10+x)(200﹣10x),
=﹣10x2+100x+2000.
故答案为:A.
【分析】设每件商品的售价上涨x元(x为正整数),则每件商品的利润为:(60﹣50+x)元,总销量为:(200﹣10x)件,根据总利润=每件商品的利润×销售量列出函数关系式即可。21·cn·jy·com?
9. 解:根据二次函数的定义可得:m2﹣2m﹣1=2,且m2﹣m≠0,
解得,m=3或m=﹣1;
当m=3时,y=6x2+9;
当m=﹣1时,y=2x2﹣4x+1;
综上所述,该二次函数的解析式为:y=6x2+9或y=2x2﹣4x+1.
【分析】利用二次函数的定义:自变量的最高次数=2,且二次项系数≠0,建立方程和不等式,求解即可的函数解析式。 21教育网?
10.解:过D作DE⊥AC于E点,如图, 设BC=a,则AC=4a, ∵∠BAD=90°,∠AED=90°, ∴∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3, 而∠ACB=90°,AB=AD, ∴△ABC≌△DAE, ∴AE=BC=a,DE=AC=4a, ∴EC=AC-AE=4a-a=3a, 在Rt△DEC中,DC=5a, ∴x=5a,即a= ?, 又∵四边形ABCD的面积y=三角形ABC的面积+三角形ACD的面积, ∴ ?, 即y与x之间的函数关系式是 . 21·世纪*教育网
【分析】过D作DE⊥AC与E点,设BC=a,则AC=4a,根据等角的余角相等可证得∠1=∠3,再证明△ABC≌△DAE,得出AE=BC=a,DE=AC=4a,就可求出EC的长,在Rt△DEC中,根据勾股定理求得DC=5a,则x=5a,即a=x,然后根据四边形ABCD的面积y=△ABC的面积+△ACD的面积,就可求出y=10a2 , 就可得出y与x之间的函数关系式。
11.(1)解:由y=﹣(m+2)xm2﹣2(m为常数),y是x的一次函数,得
,
解得m= ,
当m= 时,y是x的一次函数; (2)解:y=﹣(m+2)xm2﹣2(m为常数),是二次函数,得
,
解得m=2,m=﹣2(不符合题意的要舍去),
当m=2时,y是x的二次函数,
当y=﹣8时,﹣8=﹣4x2 ,
解得x= ,
故纵坐标为﹣8的点的坐标的坐标是( ,0).
【分析】(1)由已知y是x的一次函数,可得出x的次数=1,且x的系数≠0,就可求出m的值。 (2)根据y是x的二次函数,可知x的次数=2且x的系数≠0,求出m的值,从而可得出函数解析式,再将y=-8代入函数解析式,解关于x的方程,求出x的值,就可得出纵坐标为-8的点的坐标。?
12. (1)60;2007
(2)解:设这两年(2008-2010)绿地面积的年平均增长率为x. 21世纪教育网版权所有
60(1+x)2=72.6,
x=0.1或x=-2.1(舍去).
答:绿地面积的年平均增长率为10%.
解析:(1)从图上可看出2008年对应的绿地面积数据是60;2006年增加面积是51-48=3,2007年为56-51=5,2008年为60-56=4,故增加最多的是2007年. 2-1-c-n-j-y
故答案为60;2007. 【分析】(1)根据图中所给的信息,可得到2008年绿地的面积和增加最多的年份。 (2)根据年增长率与绿地面积的关系,可求得x的取值。21教育名师原创作品
一、基础巩固
1.函数 ( 是常数)是二次函数的条件是(?? )
A.?????????????????B.?????????????????C.?????????????????D.?
2.二次函数 的一次项系数是( ??)
A.?1??????????????????????????????????????????B.?-1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?-2
3.下列各式中,y是x的二次函数的是(??? )
A.?xy+x2=2???????????????????????????B.?x2﹣2y+2=0???????????????????????????C.?y= ???????????????? ???????????D.?y2﹣x=0
4.某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为(?? ) www.21-cn-jy.com
A.?y=100(1﹣x)2???????????????????????????????????????????????B.?y=100(1+x)2 C.?y= ??????????????????????????????????????????????????????????D.?y=100+100(1+x)+100(1+x)2
5.若 是关于自变量x的二次函数,则 ________.
6.已知函数y=(m+2)xm(m+1)是二次函数,则m=________.
二、强化提升
7.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(?? ) 21cnjy.com
A.?y=?????????????????????????????B.??? y= ?????????????????????????????C.??? y= ?????????????????????????????D.?y=
8.喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为(?? ) www-2-1-cnjy-com
A.?y=﹣10x2+100x+2000??????????????????????????????????????B.?y=10x2+100x+2000 C.?y=﹣10x2+200x???????????????????????????????????????? ??????D.?y=﹣10x2﹣100x+200021*cnjy*com
9.已知 是x的二次函数,求出它的解析式.
10.如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,求y与x之间的函数表达式. 【出处:21教育名师】
11.已知函数y=﹣(m+2)xm2﹣2(m为常数),求当m为何值时:
(1)y是x的一次函数?
(2)y是x的二次函数?并求出此时纵坐标为﹣8的点的坐标.
12.某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加。
(1)根据图中所提供的信息,回答下列问题:2008年绿地面积为________公顷。
在2006、2007、2008年这三年中,绿地面积增加最多的是________年。
(2)为了满足城市发展的需要,计划到2010年使绿地总面积达到72.6公顷,试求这两年(2008——2010)绿地面积的年平均增长率。 【版权所有:21教育】
答案解析部分
一、基础巩固
1.D
解析:根据二次函数定义中对常数a,b,c的要求,只要a≠0,b,c可以是任意实数,故答案为:D.21*cnjy*com
【分析】根据二次函数定义中对常数a,b,c的要求,只要a≠0即可。
2. D
解析:∵原二次函数可化为 ?∴其一次项系数是?2.故答案为::D.
【分析】将原函数整理成一般形式,即可得出其一次项的系数。
3.B
解析:A、整理为y= + ,不是二次函数,故不符合题意;
B、x2﹣2y+2=0变形,得y= x2+1,是二次函数,故符合题意;
C、分母中含自变量,不是二次函数,故不符合题意;
D、y的指数是2,不是函数,故不符合题意.
故答案为:B.
【分析】将A中的关系式转化为y是x的函数,即可判断;将B变形,转化为y是x的函数,利用二次函数的定义可作出判断;C中含自变量的式子是分式,不是二次函数;D中y的次数是2次,y不是x的函数,即可得出答案。2·1·c·n·j·y
4. B
解析:根据题意,由“2017年的产量=2015年的产量×(1+年平均增长率)2”得:y关于x的函数关系式为y=100(1+x)2. 故答案为:B. 【分析】根据“2017年的产量=2015年的产量×(1+年平均增长率)2”列出等量即可.
5. 2
解析:根据二次函数的定义,得:m2﹣2=2,解得:m=2或m=﹣2.
又∵m+2≠0,∴m≠﹣2,∴当m=2时,这个函数是二次函数.
故答案为:2.
【分析】根据二次函数的定义:自变量的最高指数为2,且二次项的系数不能为0,从而列出混合组,求解即可。【来源:21cnj*y.co*m】
6.1
解析:∵函数y=(m+2)xm(m+1)是二次函数, ∴ ?,
解得m=1.故答案为:1. 【分析】由于二次函数中自变量的最高指数只能为2,二次项的系数不能为0,从而列出混合组,求解即可。
二、强化提升
7. C
解析:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2 , 即(3a)2+(4a)2=x2 ,
解得:a= ,
∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF
= ×(a+4a)×4a
=10a2= x2 .
故答案为:C.
【分析】作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,利用AAS判定△ABC和△ADE全等,然后利用全等三角形的性质得出BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,利用勾股定理求出a与x的关系,分别用含x的代数式表示出DE、DF、AC,求出梯形AEDC的面积即为四边形ABCD的面积。【来源:21·世纪·教育·网】?
8. A
解析:设每件商品的售价上涨x元(x为正整数),
则每件商品的利润为:(60﹣50+x)元,
总销量为:(200﹣10x)件,
商品利润为:
y=(60﹣50+x)(200﹣10x),
=(10+x)(200﹣10x),
=﹣10x2+100x+2000.
故答案为:A.
【分析】设每件商品的售价上涨x元(x为正整数),则每件商品的利润为:(60﹣50+x)元,总销量为:(200﹣10x)件,根据总利润=每件商品的利润×销售量列出函数关系式即可。21·cn·jy·com?
9. 解:根据二次函数的定义可得:m2﹣2m﹣1=2,且m2﹣m≠0,
解得,m=3或m=﹣1;
当m=3时,y=6x2+9;
当m=﹣1时,y=2x2﹣4x+1;
综上所述,该二次函数的解析式为:y=6x2+9或y=2x2﹣4x+1.
【分析】利用二次函数的定义:自变量的最高次数=2,且二次项系数≠0,建立方程和不等式,求解即可的函数解析式。 21教育网?
10.解:过D作DE⊥AC于E点,如图, 设BC=a,则AC=4a, ∵∠BAD=90°,∠AED=90°, ∴∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3, 而∠ACB=90°,AB=AD, ∴△ABC≌△DAE, ∴AE=BC=a,DE=AC=4a, ∴EC=AC-AE=4a-a=3a, 在Rt△DEC中,DC=5a, ∴x=5a,即a= ?, 又∵四边形ABCD的面积y=三角形ABC的面积+三角形ACD的面积, ∴ ?, 即y与x之间的函数关系式是 . 21·世纪*教育网
【分析】过D作DE⊥AC与E点,设BC=a,则AC=4a,根据等角的余角相等可证得∠1=∠3,再证明△ABC≌△DAE,得出AE=BC=a,DE=AC=4a,就可求出EC的长,在Rt△DEC中,根据勾股定理求得DC=5a,则x=5a,即a=x,然后根据四边形ABCD的面积y=△ABC的面积+△ACD的面积,就可求出y=10a2 , 就可得出y与x之间的函数关系式。
11.(1)解:由y=﹣(m+2)xm2﹣2(m为常数),y是x的一次函数,得
,
解得m= ,
当m= 时,y是x的一次函数; (2)解:y=﹣(m+2)xm2﹣2(m为常数),是二次函数,得
,
解得m=2,m=﹣2(不符合题意的要舍去),
当m=2时,y是x的二次函数,
当y=﹣8时,﹣8=﹣4x2 ,
解得x= ,
故纵坐标为﹣8的点的坐标的坐标是( ,0).
【分析】(1)由已知y是x的一次函数,可得出x的次数=1,且x的系数≠0,就可求出m的值。 (2)根据y是x的二次函数,可知x的次数=2且x的系数≠0,求出m的值,从而可得出函数解析式,再将y=-8代入函数解析式,解关于x的方程,求出x的值,就可得出纵坐标为-8的点的坐标。?
12. (1)60;2007
(2)解:设这两年(2008-2010)绿地面积的年平均增长率为x. 21世纪教育网版权所有
60(1+x)2=72.6,
x=0.1或x=-2.1(舍去).
答:绿地面积的年平均增长率为10%.
解析:(1)从图上可看出2008年对应的绿地面积数据是60;2006年增加面积是51-48=3,2007年为56-51=5,2008年为60-56=4,故增加最多的是2007年. 2-1-c-n-j-y
故答案为60;2007. 【分析】(1)根据图中所给的信息,可得到2008年绿地的面积和增加最多的年份。 (2)根据年增长率与绿地面积的关系,可求得x的取值。21教育名师原创作品
同课章节目录
