人教版数学八年级上册课件 11.2.1三角形的内角和 课件(35张PPT)
文档属性
| 名称 | 人教版数学八年级上册课件 11.2.1三角形的内角和 课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 611.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 17:27:00 | ||
图片预览



文档简介
课件35张PPT。﹙一﹚什么是三角形与三角形的表示方法。
﹙二﹚三角形中的主要线段。
﹙三﹚三角形三边的关系。
知识回顾请同学们自己任意画一个三角形,三个内角的度数是多少度?小组交流猜猜看?如何证明这个结论的正确性?结论:三角形的内角和等于180 °已知:△A B C.
求证:∠A +∠B +∠C =180°证法一证法三证法二证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一A.B.已知:△A B C.
求证:∠A +∠B +∠C=180°证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.E.D.证法一返回证法一 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚已知:△A B C.
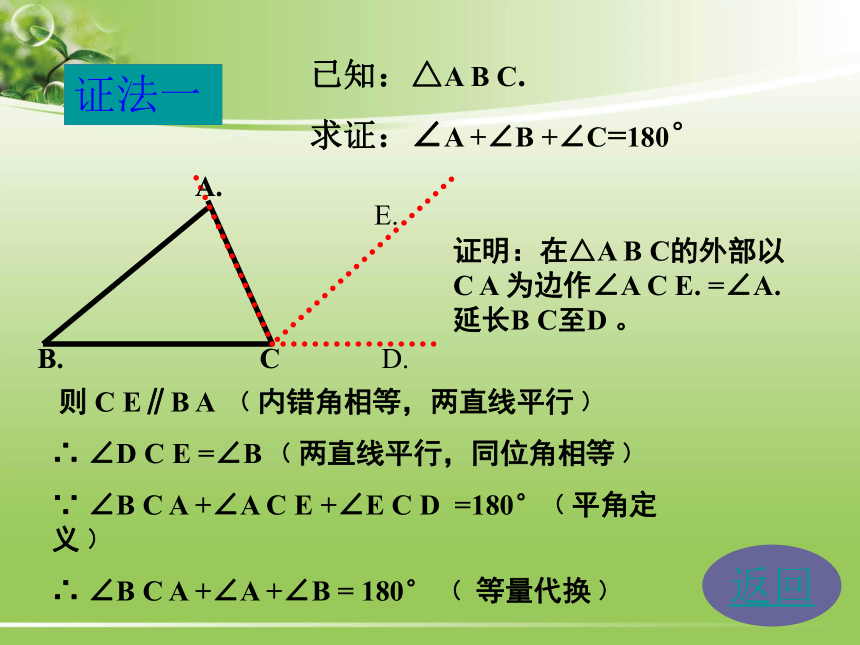
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E. =∠A. 延长B C至D 。A.B.E.D.证法一返回证法一已知:△A B C.
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E. =∠A. 延长B C至D 。 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚A.B.证法二返回已知:△A B C.
求证:∠A +∠B +∠C =180°E. 证明:延长B C至D ,过C作C E∥B A. 则∠ A =∠A C E ﹙两直线平行,内错角相等﹚
∠ B =∠E C D ﹙两直线平行,同位角相等﹚
∵ ∠ B C A +∠A C E +∠E C D =180° ﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚ A.B.证法二返回已知:△A B C.
求证:∠A +∠B +∠C =180°E. 证明:延长B C至D ,过C作C E∥B A. 则∠ A =∠A C E ﹙两直线平行,内错角相等﹚
∠ B =∠E C D ﹙两直线平行,同位角相等﹚
∵ ∠ B C A +∠A C E +∠E C D =180° ﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚ A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.E.证法三证明:过A 作E F∥B C.
则∠E A B =∠B.
∠F A C = ∠C ﹙两直线平行,内错角相等﹚ ∵∠E A B +∠B A C +∠C A F =180°
∴ ∠B +∠B A C +∠C= 180° ﹙ 等量代换﹚ F 返回已知:△A B C.
求证:∠A +∠B +∠C =180°1.三角形内角和定理: 三角形的内角和等于180°。
即:△ABC中, ∠A +∠B +∠C=180 °
2.推论: 直角三角形中,两锐角互余。
即: 直角 △A B C 中∠C =90°,
则∠A +∠B =90 °定理应用 三角形的三内角和是180o ,所以三内角可能出现的情况:一个钝角 两个锐角钝角三角形锐角三角形一个直角 两个锐角直角三角形三个都为锐角例1.在△ABC中:①∠A=35°, ∠C=90 °,则∠B=?
②∠A=50°,∠B=∠C,则∠B=?
③ ∠A : ∠B :∠C=3:2:1,问 △ABC是什么三角形?
④ ∠A -∠C =35 °,∠B -∠C =10 °, 则∠B =?例2.在△ABC中, ∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。解:△A B C 中,设∠A = x ,则
∠C =∠A B C = 2x
x + 2x + 2x =180°(三角形内角和为180 °)
x=36 °
∠C =2x = 72 °
在△B C D 中,∠B D C =90 °
则∠ D B C = 90 °- ∠C =18 °
﹙直角三角形两锐角互余﹚A. BCDB.CD.1、一个三角形最多有 个直角,最多有 个
钝角。
2、在△ABC中,若∠A+∠B=2∠C,则∠C= 。
3、若一个三角形的三个内角之比为2:3:4,则
这三个内角的度数为 。
4、如图:∠α= 。
13201440α480600400,600,800280课堂反馈1.在△ABC中,∠BAC=90°,AD⊥BC,则图中互为余角的角有几对?自我挑战2.△A B C中,∠A =∠B +∠C,问△A B C是什么三角形?3. △A B C 中,∠C =2 (∠B +∠A ), 求∠C 的度数。自我挑战对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?畅所欲言小结作业:
第3、4题
1.三角形内角和定理的证明。
2.三角形内角和定理与推论。
3.三角形内角和定理与推论的运用。谢谢 再见
﹙二﹚三角形中的主要线段。
﹙三﹚三角形三边的关系。
知识回顾请同学们自己任意画一个三角形,三个内角的度数是多少度?小组交流猜猜看?如何证明这个结论的正确性?结论:三角形的内角和等于180 °已知:△A B C.
求证:∠A +∠B +∠C =180°证法一证法三证法二证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一A.B.已知:△A B C.
求证:∠A +∠B +∠C=180°证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.证法一已知:△A B C.
求证:∠A +∠B +∠C=180°A.B.E.D.证法一返回证法一 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚已知:△A B C.
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E. =∠A. 延长B C至D 。A.B.E.D.证法一返回证法一已知:△A B C.
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E. =∠A. 延长B C至D 。 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚A.B.证法二返回已知:△A B C.
求证:∠A +∠B +∠C =180°E. 证明:延长B C至D ,过C作C E∥B A. 则∠ A =∠A C E ﹙两直线平行,内错角相等﹚
∠ B =∠E C D ﹙两直线平行,同位角相等﹚
∵ ∠ B C A +∠A C E +∠E C D =180° ﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚ A.B.证法二返回已知:△A B C.
求证:∠A +∠B +∠C =180°E. 证明:延长B C至D ,过C作C E∥B A. 则∠ A =∠A C E ﹙两直线平行,内错角相等﹚
∠ B =∠E C D ﹙两直线平行,同位角相等﹚
∵ ∠ B C A +∠A C E +∠E C D =180° ﹙平角定义﹚
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚ A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.已知:△A B C.
求证:∠A +∠B +∠C =180°证法三A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.证法三已知:△A B C.
求证:∠A +∠B +∠C =180°A.B.E.证法三证明:过A 作E F∥B C.
则∠E A B =∠B.
∠F A C = ∠C ﹙两直线平行,内错角相等﹚ ∵∠E A B +∠B A C +∠C A F =180°
∴ ∠B +∠B A C +∠C= 180° ﹙ 等量代换﹚ F 返回已知:△A B C.
求证:∠A +∠B +∠C =180°1.三角形内角和定理: 三角形的内角和等于180°。
即:△ABC中, ∠A +∠B +∠C=180 °
2.推论: 直角三角形中,两锐角互余。
即: 直角 △A B C 中∠C =90°,
则∠A +∠B =90 °定理应用 三角形的三内角和是180o ,所以三内角可能出现的情况:一个钝角 两个锐角钝角三角形锐角三角形一个直角 两个锐角直角三角形三个都为锐角例1.在△ABC中:①∠A=35°, ∠C=90 °,则∠B=?
②∠A=50°,∠B=∠C,则∠B=?
③ ∠A : ∠B :∠C=3:2:1,问 △ABC是什么三角形?
④ ∠A -∠C =35 °,∠B -∠C =10 °, 则∠B =?例2.在△ABC中, ∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。解:△A B C 中,设∠A = x ,则
∠C =∠A B C = 2x
x + 2x + 2x =180°(三角形内角和为180 °)
x=36 °
∠C =2x = 72 °
在△B C D 中,∠B D C =90 °
则∠ D B C = 90 °- ∠C =18 °
﹙直角三角形两锐角互余﹚A. BCDB.CD.1、一个三角形最多有 个直角,最多有 个
钝角。
2、在△ABC中,若∠A+∠B=2∠C,则∠C= 。
3、若一个三角形的三个内角之比为2:3:4,则
这三个内角的度数为 。
4、如图:∠α= 。
13201440α480600400,600,800280课堂反馈1.在△ABC中,∠BAC=90°,AD⊥BC,则图中互为余角的角有几对?自我挑战2.△A B C中,∠A =∠B +∠C,问△A B C是什么三角形?3. △A B C 中,∠C =2 (∠B +∠A ), 求∠C 的度数。自我挑战对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?畅所欲言小结作业:
第3、4题
1.三角形内角和定理的证明。
2.三角形内角和定理与推论。
3.三角形内角和定理与推论的运用。谢谢 再见
