人教版八年级数学上册第十一章三角形 11.2.2三角形的外角课件(共27张)
文档属性
| 名称 | 人教版八年级数学上册第十一章三角形 11.2.2三角形的外角课件(共27张) | 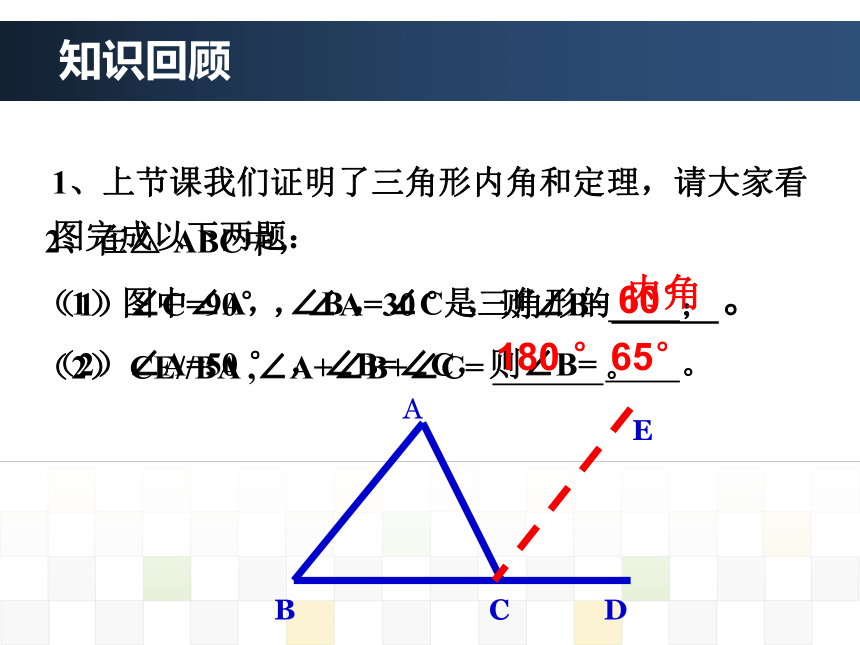 | |
| 格式 | zip | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 07:14:13 | ||
图片预览



文档简介
课件27张PPT。2、在△ ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= 。(1)图中∠A, ∠B ,∠C是三角形的 。
(2) CE//BA ,∠A+∠B+∠C= 。
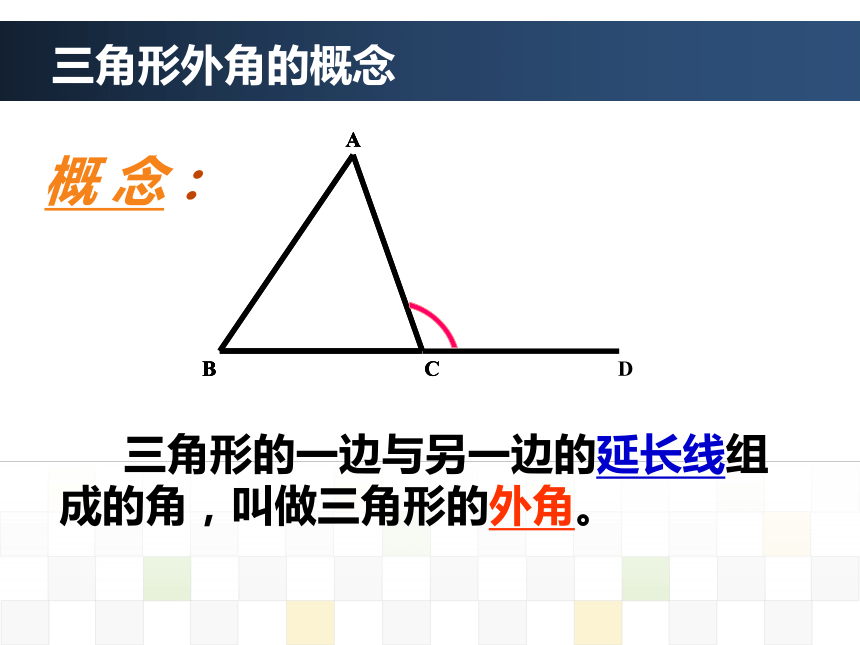
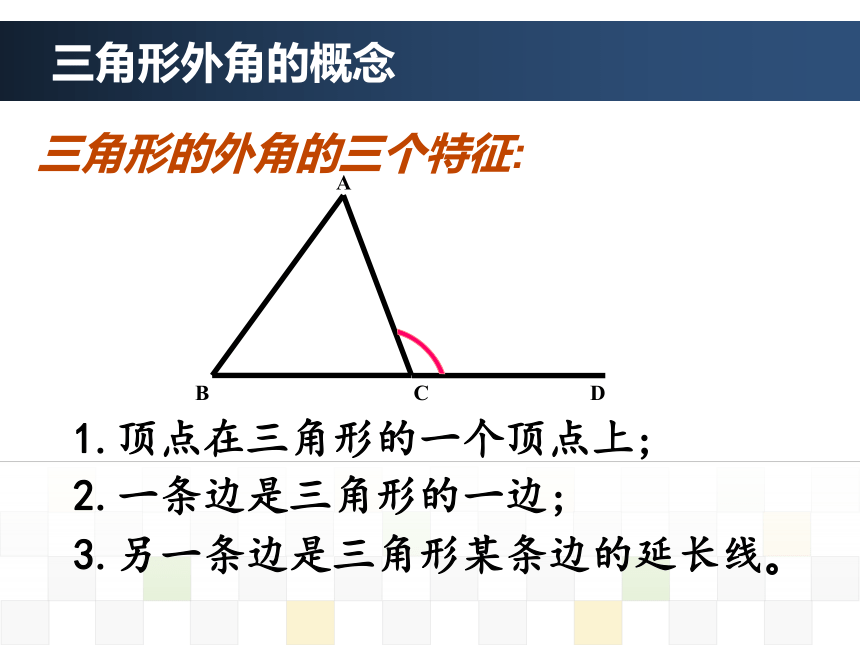
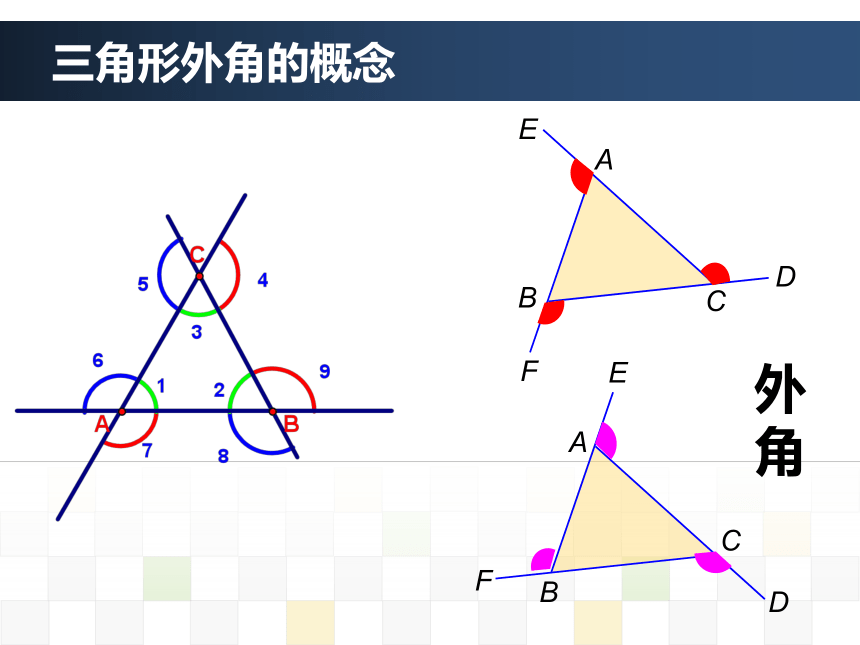
知识回顾1、上节课我们证明了三角形内角和定理,请大家看图完成以下两题: 内角180 °60°65°教材版本:2013年人教版 年 级:八年级(上) 主讲教师:张 丽 萍11.2.2 三角形的外角大名县回民中学学习内容1 三角形外角的概念三角形外角的概念ABCDABCAB 三角形的一边与另一边的延长线组成的角,叫做三角形的外角。概 念:三角形的外角的三个特征:
1.顶点在三角形的一个顶点上;
2.一条边是三角形的一边;
3.另一条边是三角形某条边的延长线。三角形外角的概念画一个三角形,再画出它所有的外角。想一想:
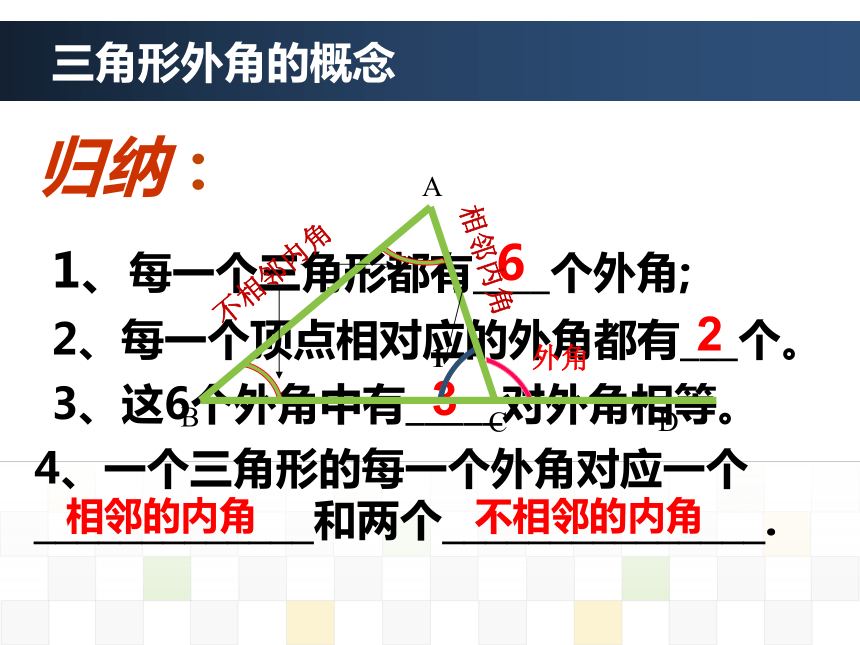
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几对外角相等? 4、三角形的每一个外角与三角形的三个内角有怎样的位置关系?三角形外角的概念外角三角形外角的概念1、每一个三角形都有____个外角;62、每一个顶点相对应的外角都有___个。23、这6个外角中有_____对外角相等。3 4、一个三角形的每一个外角对应一个
_____________和两个_______________.相邻的内角不相邻的内角归纳:三角形外角的概念学习内容2 三角形外角的性质
∠ACD和∠ACB有什么位置关系?
∠ACD和∠ACB有什么数量关系?
∠ACD与∠BAC, ∠B的位置是怎样的?
∠ACD与∠BAC, ∠B的大小有什么关系?三角形的一个外角等于与它不相邻的两个内角的和。探索与证明三角形外角的性质图中哪些角是三角形的内角,
哪些角是三角形的外角?115°125°65°算一算:看一看:∠ACB ,∠ACD ,∠CAE想一想:结论:已知:如图: △ABC中,点D在BC的延长上。
求证:∠ACD =∠A+∠B。探索与证明三角形外角的性质探究:你能用推理的方法来论证∠ACD= ∠A + ∠B 吗?你能用几种方法呢?相信你一定能行!探索与证明三角形外角的性质 ∵∠ACD+ ∠ACB=180°又∵∠A+ ∠B+ ∠ACB=180° ∴ ∠ACD = ∠A+ ∠B解:∴∠ACD =180 ° -∠ACB ∴∠A+ ∠B =180 °-∠ACB(邻补角的定义)(三角形内角和定理 )(等量代换)方法一:探索与证明三角形外角的性质方法二:擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?ABCD(CE//BA)E探索与证明三角形外角的性质∵∠ACD= ∠A+ ∠B∴ ∠ACD ∠A (<、>)
∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相邻的内角。议一议:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?与同桌交流一下。>>探索与证明三角形外角的性质三角形外角的性质:归 纳★ ★三角形的一个外角等于与它不相邻的两个内角的和。 ∠ACD= ∠A+ ∠B★ ★三角形的一个外角大于任何一个与它不相邻的内角。
∠ACD > ∠A ,∠ACD > ∠B。 学习内容3 三角形外角性质的应用 三角形外角性质的应用例 4:如图, ∠BAE, ∠CBF, ∠ACD是△ ABC的三个外角,它们的和是多少?解:由三角形的一个外角等于与它∠BAE=
∠CBF=
∠ACD=∠BAE+ ∠CBF+ ∠ACD=
所以由∠1+ ∠2 + ∠3 = 180°,得
∠BAE+ ∠CBF+ ∠ACD= 2× 180°=360°
不相邻的两个内角的和,得
三角形外角和等于360°∠2 +∠3∠1 +∠3∠1 +∠22(∠1+ ∠2 + ∠3 )练习巩固1.求下列各图中∠1的度数。∠1= ∠1= 85o95o练一练:2. 如图所示, ∠A=37°,∠CBE=155°,
求∠1,∠2,∠3的度数。∠1=25°,∠2=62°,∠3=118°练习巩固3.把图中∠1、∠2、∠3按由大到小的顺序排列。∠1>>∠2∠3练习巩固 4.在三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠ 1, ∠ 2,∠ 3),那么回到原来位置时,一共转了几度?
练习巩固 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。国旗上的数学拓展与思考:练习巩固学习内容 小 结 课堂小结1.三角形外角的概念;
2.三角形外角的两个性质;3.三角形的外角和等于360o。作业教材书习题11.2第6、8题作业布置谢谢
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= 。(1)图中∠A, ∠B ,∠C是三角形的 。
(2) CE//BA ,∠A+∠B+∠C= 。
知识回顾1、上节课我们证明了三角形内角和定理,请大家看图完成以下两题: 内角180 °60°65°教材版本:2013年人教版 年 级:八年级(上) 主讲教师:张 丽 萍11.2.2 三角形的外角大名县回民中学学习内容1 三角形外角的概念三角形外角的概念ABCDABCAB 三角形的一边与另一边的延长线组成的角,叫做三角形的外角。概 念:三角形的外角的三个特征:
1.顶点在三角形的一个顶点上;
2.一条边是三角形的一边;
3.另一条边是三角形某条边的延长线。三角形外角的概念画一个三角形,再画出它所有的外角。想一想:
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几对外角相等? 4、三角形的每一个外角与三角形的三个内角有怎样的位置关系?三角形外角的概念外角三角形外角的概念1、每一个三角形都有____个外角;62、每一个顶点相对应的外角都有___个。23、这6个外角中有_____对外角相等。3 4、一个三角形的每一个外角对应一个
_____________和两个_______________.相邻的内角不相邻的内角归纳:三角形外角的概念学习内容2 三角形外角的性质
∠ACD和∠ACB有什么位置关系?
∠ACD和∠ACB有什么数量关系?
∠ACD与∠BAC, ∠B的位置是怎样的?
∠ACD与∠BAC, ∠B的大小有什么关系?三角形的一个外角等于与它不相邻的两个内角的和。探索与证明三角形外角的性质图中哪些角是三角形的内角,
哪些角是三角形的外角?115°125°65°算一算:看一看:∠ACB ,∠ACD ,∠CAE想一想:结论:已知:如图: △ABC中,点D在BC的延长上。
求证:∠ACD =∠A+∠B。探索与证明三角形外角的性质探究:你能用推理的方法来论证∠ACD= ∠A + ∠B 吗?你能用几种方法呢?相信你一定能行!探索与证明三角形外角的性质 ∵∠ACD+ ∠ACB=180°又∵∠A+ ∠B+ ∠ACB=180° ∴ ∠ACD = ∠A+ ∠B解:∴∠ACD =180 ° -∠ACB ∴∠A+ ∠B =180 °-∠ACB(邻补角的定义)(三角形内角和定理 )(等量代换)方法一:探索与证明三角形外角的性质方法二:擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?ABCD(CE//BA)E探索与证明三角形外角的性质∵∠ACD= ∠A+ ∠B∴ ∠ACD ∠A (<、>)
∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相邻的内角。议一议:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?与同桌交流一下。>>探索与证明三角形外角的性质三角形外角的性质:归 纳★ ★三角形的一个外角等于与它不相邻的两个内角的和。 ∠ACD= ∠A+ ∠B★ ★三角形的一个外角大于任何一个与它不相邻的内角。
∠ACD > ∠A ,∠ACD > ∠B。 学习内容3 三角形外角性质的应用 三角形外角性质的应用例 4:如图, ∠BAE, ∠CBF, ∠ACD是△ ABC的三个外角,它们的和是多少?解:由三角形的一个外角等于与它∠BAE=
∠CBF=
∠ACD=∠BAE+ ∠CBF+ ∠ACD=
所以由∠1+ ∠2 + ∠3 = 180°,得
∠BAE+ ∠CBF+ ∠ACD= 2× 180°=360°
不相邻的两个内角的和,得
三角形外角和等于360°∠2 +∠3∠1 +∠3∠1 +∠22(∠1+ ∠2 + ∠3 )练习巩固1.求下列各图中∠1的度数。∠1= ∠1= 85o95o练一练:2. 如图所示, ∠A=37°,∠CBE=155°,
求∠1,∠2,∠3的度数。∠1=25°,∠2=62°,∠3=118°练习巩固3.把图中∠1、∠2、∠3按由大到小的顺序排列。∠1>>∠2∠3练习巩固 4.在三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠ 1, ∠ 2,∠ 3),那么回到原来位置时,一共转了几度?
练习巩固 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。国旗上的数学拓展与思考:练习巩固学习内容 小 结 课堂小结1.三角形外角的概念;
2.三角形外角的两个性质;3.三角形的外角和等于360o。作业教材书习题11.2第6、8题作业布置谢谢
