2019-2020学年高中数学新人教B版必修1课件:第1章集合1.1.1集合的概念(27张)
文档属性
| 名称 | 2019-2020学年高中数学新人教B版必修1课件:第1章集合1.1.1集合的概念(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览








文档简介
课件27张PPT。第一章 集合1.1 集合与集合的表示方法1.1.1 集合的概念1.了解集合的含义,会用符号“∈”或“?”表示元素与集合之间的关系.
2.理解集合中元素的特性,重点理解其确定性与互异性.
3.熟悉常用数集的符号,尤其要注意空集的含义及表示.123451.集合的有关概念
一般地,把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集),通常用英语大写字母A,B,C,…来表示.构成集合的每个对象叫做这个集合的元素(或成员),通常用英语小写字母a,b,c,…来表示.
名师点拨集合是现代数学中不加定义的基本概念,学习这个概念应注意以下两点:
(1)集合是一个“整体”;
(2)构成集合的对象必须是“确定”且“不同”的.12345【做一做1】 下列各组对象不能构成集合的是( )
A.著名的中国数学家
B.所有的负数
C.清华大学招收的2016级本科生
D.某次会议所有的代表
解析:因为选项B,C,D中所给的对象都是确定的,所以可以构成集合;而选项A中所给对象不确定,原因是没有具体的标准来衡量一位数学家怎样才算著名,故不能构成集合.
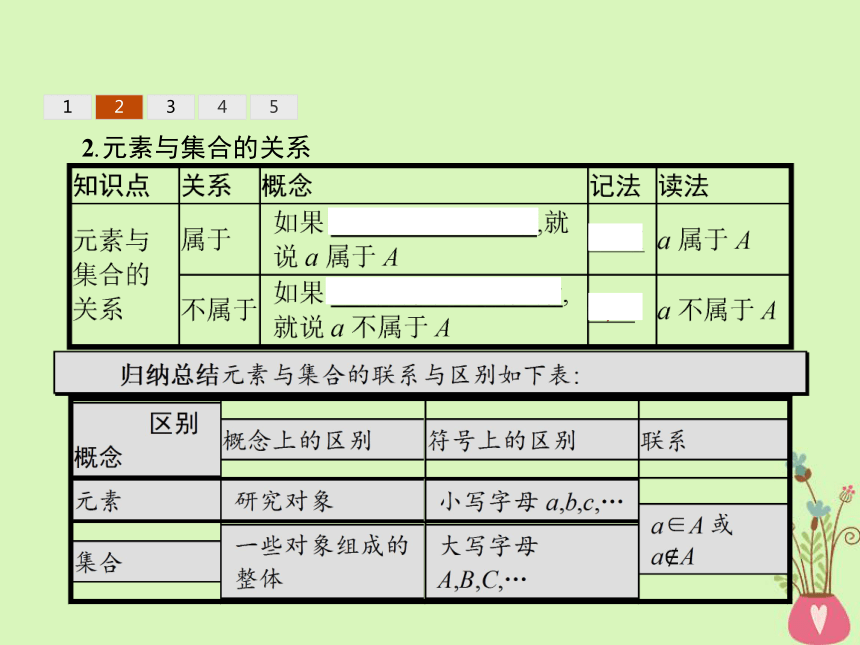
答案:A123452.元素与集合的关系 12345123453.集合中元素的性质特征
(1)确定性;(2)互异性;(3)无序性.
名师点拨在处理集合中有关元素的问题时,求得其中元素(或字母)的值以后,要充分考虑集合元素的互异性与分类讨论思想的应用,要进行代入检验,舍去不符合要求的值.12345【做一做3-1】 若a,a,b,b,a2,b2构成集合M,则M中的元素最多有( )个.
A.6 B.5
C.4 D.3
解析:由集合元素的互异性可知,当a,b,a2,b2互不相等时,集合M中的元素最多,即集合M最多有4个元素.
答案:C
【做一做3-2】 方程x2-2x+1=0的解集中有 个元素.?
答案:1124354.集合的分类
【做一做4】 指出下列集合是有限集还是无限集:
(1)满足2 015(2)数轴上所有的实数对应的点构成的集合.
解:(1)满足2 015(2)数轴上实数对应的点有无穷多个,故此集合是无限集.124355.常用数集及表示符号
【做一做5】 下列关系表示正确的是( )
A.0∈N+ B.π?R
C.1?Q D.0∈Z
答案:D一、集合中元素的特性
剖析:确定性:作为一个集合的元素,必须是确定的.这就是说,不能确定的对象就不能构成集合.也就是说,给定一个集合,任何一个对象是不是这个集合的元素也就确定了.
互异性:对于一个给定的集合,集合中的元素一定是不同的(或说是互异的).这就是说,集合中的任何两个元素都是不同的对象,相同的对象归入同一个集合时只能算作集合的一个元素.
无序性:集合中的元素没有顺序,在表示集合时先写哪个元素都可以.
二、特殊集合——空集
剖析:我们把不含任何元素的集合叫做空集,记作?.空集是一个实实在在的集合,只不过此集合中没有任何元素,故称为空集.例如,由“方程x2+2=0的实数根”构成的集合,因为没有适合该集合的元素,所以它是空集.名师点拨1.空集的本质是其不含有任何元素,它的表现形式是多种多样的.例如,由所有平方等于-1的实数构成的集合;由所有大于-3且小于0的自然数构成的集合;由所有的有两个内角是直角的三角形构成的集合等都是空集.
2.不要将实数0或只含一个元素0的集合与空集?混为一谈.实数0只能作为元素出现,它不是集合,只含一个元素0的集合不等同于?,因为它含有元素.三、教材中的“思考与讨论”
1.你能否确定,你所在班级中,高个子同学构成的集合?并说明理由.
剖析:不能确定.原因是对高个子同学“高”的程度没有确定的标准,所以无法判定哪些同学符合要求,因此不能构成集合.
2.你能否确定,你所在班级中,最高的3位同学构成的集合?
剖析:能确定.因为班里最高的3位同学是确定的(只要按身高从高到低取前三名即可),将他们作为元素放在一起即构成所要求的集合.【例1】 下列各组对象能构成集合吗?
(1)你所在班级的男生;
(2)参加2016年第31届夏季奥林匹克运动会的高大运动员;
(3)关于x的方程x2+5=0的实数解;
(4)所有小的正数;
(5)到两定点距离的和等于两定点间的距离的点.
解:(1)(3)(5)可以构成集合;(2)(4)不能构成集合.
反思看一组对象能否构成一个集合,只要看这组对象是不是确定的,即任何一个对象,要么在这一组对象中,要么不在这组对象中,而没有第三种情况出现.题型一题型二题型三题型一题型二题型三【变式训练1】 给出以下各组对象:①较大的正整数;②北京市所有身高为1.75米的人;③美国NBA的著名球星;④方程x2=4的所有实数解;⑤小于1的正整数.其中能构成集合的对象的组数为( )
A.2 B.3
C.4 D.5
解析:“较大”和“著名”没有确定的标准,所以①和③不能构成集合,②④⑤均可构成集合.
答案:B题型一题型二题型三【例2】 由元素3,x,x2-2x构成集合M,则x应满足的条件是 .?
答案:x≠3,且x≠0,且x≠-1
反思互异性是集合元素的重要性质,在解决集合中有关元素的问题时,一定要注意利用元素的互异性进行验证.题型一题型二题型三【变式训练2】 由方程x2-5x+6=0和方程x2-x-2=0的所有实数根构成的集合中,元素的个数为( )
A.1 B.2
C.3 D.4
解析:方程x2-5x+6=0的根是2和3,方程x2-x-2=0的根是2和-1,因此两个方程的所有实数根构成的集合中含有3个元素2,3,-1.
答案:C题型一题型二题型三【例3】 已知集合P中有三个元素a-3,2a-1,a2+4,且-3∈P,求实数a的值.
分析:利用-3是集合P中的元素,可列方程求a的值,最后需验证集合中元素的互异性.
解:因为-3∈P,a2+4≥4,
所以a-3=-3或2a-1=-3,
解得a=0或a=-1.
经检验,当a=0时,P中三个元素为-3,-1,4,满足集合中元素的互异性;
当a=-1时,P中三个元素为-4,-3,5,也满足集合中元素的互异性.
综上可知,a的值为0或-1.
反思在根据元素与集合的关系解题时,要注意将求得的参数值代入检验,看是否符合题意及元素的互异性等性质.题型一题型二题型三【变式训练3】 在例3所给的集合P中,是否含有元素-5?
解:不含有元素-5.理由如下:
若-5∈P,由于a2+4≥4,
故只能有a-3=-5或2a-1=-5,
这时a=-2,但a-3=2a-1=-5,不满足集合中元素的互异性.
因此,集合P中不可能含有元素-5.1 2 3 4 5 61下列各组对象,能构成集合的是( )
A.平面直角坐标系内x轴上方的y轴附近的点
B.平面内两边之和小于第三边的三角形
C.某书店中有意义的小说
D.π(π=3.141…)的近似值的全体
解析:选项A,C,D中的对象不具有确定性,故不能构成集合;而选项B为?,故能构成集合.
答案:B1 2 3 4 5 6
其中正确的个数为( )
A.1 B.2 C.3 D.4
解析:①②正确,③④错误.
答案:B1 2 3 4 5 63由a2,2-a,4组成一个集合A,且集合A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2
C.6 D.2
解析:代入验证如下:当a=1时,a2=2-a;
当a=-2时,a2=2-a=4;
当a=2时,a2=4;故1,-2,2均不能满足集合A中元素的互异性,排除选项A,B,D;当a=6时,a2=36,2-a=-4,符合要求,故选C.
答案:C1 2 3 4 5 64集合A是由点(2 017,2 016)和点(2 016,2 017)构成的,则A中有 个元素.?
解析:因为点的坐标是有顺序性的,所以集合A中有2个点,即A中有2个元素.
答案:21 2 3 4 5 65设L(A,B)表示直线AB上所有点组成的集合,“P是直线AB上的一个点”这句话就可以简单地写成P L(A,B).?
答案:∈1 2 3 4 5 66已知集合A由三个元素a2,a+1,0构成,且1∈A,试求实数a的值.
解:因为1∈A,所以a2=1或a+1=1.
若a2=1,则a=±1.
当a=1时,集合A中的元素是1,2,0,符合要求;
当a=-1时,集合A中的元素是1,0,0,不符合元素的互异性.
若a+1=1,则a=0,集合A中的元素是0,1,0,不符合元素的互异性.
综上可知,实数a的值为1.
2.理解集合中元素的特性,重点理解其确定性与互异性.
3.熟悉常用数集的符号,尤其要注意空集的含义及表示.123451.集合的有关概念
一般地,把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集),通常用英语大写字母A,B,C,…来表示.构成集合的每个对象叫做这个集合的元素(或成员),通常用英语小写字母a,b,c,…来表示.
名师点拨集合是现代数学中不加定义的基本概念,学习这个概念应注意以下两点:
(1)集合是一个“整体”;
(2)构成集合的对象必须是“确定”且“不同”的.12345【做一做1】 下列各组对象不能构成集合的是( )
A.著名的中国数学家
B.所有的负数
C.清华大学招收的2016级本科生
D.某次会议所有的代表
解析:因为选项B,C,D中所给的对象都是确定的,所以可以构成集合;而选项A中所给对象不确定,原因是没有具体的标准来衡量一位数学家怎样才算著名,故不能构成集合.
答案:A123452.元素与集合的关系 12345123453.集合中元素的性质特征
(1)确定性;(2)互异性;(3)无序性.
名师点拨在处理集合中有关元素的问题时,求得其中元素(或字母)的值以后,要充分考虑集合元素的互异性与分类讨论思想的应用,要进行代入检验,舍去不符合要求的值.12345【做一做3-1】 若a,a,b,b,a2,b2构成集合M,则M中的元素最多有( )个.
A.6 B.5
C.4 D.3
解析:由集合元素的互异性可知,当a,b,a2,b2互不相等时,集合M中的元素最多,即集合M最多有4个元素.
答案:C
【做一做3-2】 方程x2-2x+1=0的解集中有 个元素.?
答案:1124354.集合的分类
【做一做4】 指出下列集合是有限集还是无限集:
(1)满足2 015
解:(1)满足2 015
【做一做5】 下列关系表示正确的是( )
A.0∈N+ B.π?R
C.1?Q D.0∈Z
答案:D一、集合中元素的特性
剖析:确定性:作为一个集合的元素,必须是确定的.这就是说,不能确定的对象就不能构成集合.也就是说,给定一个集合,任何一个对象是不是这个集合的元素也就确定了.
互异性:对于一个给定的集合,集合中的元素一定是不同的(或说是互异的).这就是说,集合中的任何两个元素都是不同的对象,相同的对象归入同一个集合时只能算作集合的一个元素.
无序性:集合中的元素没有顺序,在表示集合时先写哪个元素都可以.
二、特殊集合——空集
剖析:我们把不含任何元素的集合叫做空集,记作?.空集是一个实实在在的集合,只不过此集合中没有任何元素,故称为空集.例如,由“方程x2+2=0的实数根”构成的集合,因为没有适合该集合的元素,所以它是空集.名师点拨1.空集的本质是其不含有任何元素,它的表现形式是多种多样的.例如,由所有平方等于-1的实数构成的集合;由所有大于-3且小于0的自然数构成的集合;由所有的有两个内角是直角的三角形构成的集合等都是空集.
2.不要将实数0或只含一个元素0的集合与空集?混为一谈.实数0只能作为元素出现,它不是集合,只含一个元素0的集合不等同于?,因为它含有元素.三、教材中的“思考与讨论”
1.你能否确定,你所在班级中,高个子同学构成的集合?并说明理由.
剖析:不能确定.原因是对高个子同学“高”的程度没有确定的标准,所以无法判定哪些同学符合要求,因此不能构成集合.
2.你能否确定,你所在班级中,最高的3位同学构成的集合?
剖析:能确定.因为班里最高的3位同学是确定的(只要按身高从高到低取前三名即可),将他们作为元素放在一起即构成所要求的集合.【例1】 下列各组对象能构成集合吗?
(1)你所在班级的男生;
(2)参加2016年第31届夏季奥林匹克运动会的高大运动员;
(3)关于x的方程x2+5=0的实数解;
(4)所有小的正数;
(5)到两定点距离的和等于两定点间的距离的点.
解:(1)(3)(5)可以构成集合;(2)(4)不能构成集合.
反思看一组对象能否构成一个集合,只要看这组对象是不是确定的,即任何一个对象,要么在这一组对象中,要么不在这组对象中,而没有第三种情况出现.题型一题型二题型三题型一题型二题型三【变式训练1】 给出以下各组对象:①较大的正整数;②北京市所有身高为1.75米的人;③美国NBA的著名球星;④方程x2=4的所有实数解;⑤小于1的正整数.其中能构成集合的对象的组数为( )
A.2 B.3
C.4 D.5
解析:“较大”和“著名”没有确定的标准,所以①和③不能构成集合,②④⑤均可构成集合.
答案:B题型一题型二题型三【例2】 由元素3,x,x2-2x构成集合M,则x应满足的条件是 .?
答案:x≠3,且x≠0,且x≠-1
反思互异性是集合元素的重要性质,在解决集合中有关元素的问题时,一定要注意利用元素的互异性进行验证.题型一题型二题型三【变式训练2】 由方程x2-5x+6=0和方程x2-x-2=0的所有实数根构成的集合中,元素的个数为( )
A.1 B.2
C.3 D.4
解析:方程x2-5x+6=0的根是2和3,方程x2-x-2=0的根是2和-1,因此两个方程的所有实数根构成的集合中含有3个元素2,3,-1.
答案:C题型一题型二题型三【例3】 已知集合P中有三个元素a-3,2a-1,a2+4,且-3∈P,求实数a的值.
分析:利用-3是集合P中的元素,可列方程求a的值,最后需验证集合中元素的互异性.
解:因为-3∈P,a2+4≥4,
所以a-3=-3或2a-1=-3,
解得a=0或a=-1.
经检验,当a=0时,P中三个元素为-3,-1,4,满足集合中元素的互异性;
当a=-1时,P中三个元素为-4,-3,5,也满足集合中元素的互异性.
综上可知,a的值为0或-1.
反思在根据元素与集合的关系解题时,要注意将求得的参数值代入检验,看是否符合题意及元素的互异性等性质.题型一题型二题型三【变式训练3】 在例3所给的集合P中,是否含有元素-5?
解:不含有元素-5.理由如下:
若-5∈P,由于a2+4≥4,
故只能有a-3=-5或2a-1=-5,
这时a=-2,但a-3=2a-1=-5,不满足集合中元素的互异性.
因此,集合P中不可能含有元素-5.1 2 3 4 5 61下列各组对象,能构成集合的是( )
A.平面直角坐标系内x轴上方的y轴附近的点
B.平面内两边之和小于第三边的三角形
C.某书店中有意义的小说
D.π(π=3.141…)的近似值的全体
解析:选项A,C,D中的对象不具有确定性,故不能构成集合;而选项B为?,故能构成集合.
答案:B1 2 3 4 5 6
其中正确的个数为( )
A.1 B.2 C.3 D.4
解析:①②正确,③④错误.
答案:B1 2 3 4 5 63由a2,2-a,4组成一个集合A,且集合A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2
C.6 D.2
解析:代入验证如下:当a=1时,a2=2-a;
当a=-2时,a2=2-a=4;
当a=2时,a2=4;故1,-2,2均不能满足集合A中元素的互异性,排除选项A,B,D;当a=6时,a2=36,2-a=-4,符合要求,故选C.
答案:C1 2 3 4 5 64集合A是由点(2 017,2 016)和点(2 016,2 017)构成的,则A中有 个元素.?
解析:因为点的坐标是有顺序性的,所以集合A中有2个点,即A中有2个元素.
答案:21 2 3 4 5 65设L(A,B)表示直线AB上所有点组成的集合,“P是直线AB上的一个点”这句话就可以简单地写成P L(A,B).?
答案:∈1 2 3 4 5 66已知集合A由三个元素a2,a+1,0构成,且1∈A,试求实数a的值.
解:因为1∈A,所以a2=1或a+1=1.
若a2=1,则a=±1.
当a=1时,集合A中的元素是1,2,0,符合要求;
当a=-1时,集合A中的元素是1,0,0,不符合元素的互异性.
若a+1=1,则a=0,集合A中的元素是0,1,0,不符合元素的互异性.
综上可知,实数a的值为1.
