2019-2020学年高中数学新人教B版必修1课件:第1章集合1.2.2.2补集(31张)
文档属性
| 名称 | 2019-2020学年高中数学新人教B版必修1课件:第1章集合1.2.2.2补集(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 488.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览










文档简介
课件31张PPT。第2课时 补集1.在具体情境中,了解全集的含义.
2.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
3.重视补集思想在解题中的应用.121.全集与补集
如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示.
如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记作?UA,读作“A在U中的补集”.12归纳总结1.补集的符号语言为:?UA={x|x∈U,且x?A};
2.补集的维恩(Venn)图表示如图所示;
3.全集具有相对性,即研究某个问题时的全集可能在研究另一个问题时就不是全集.补集是相对于全集而言的,由于全集具有相对性,那么补集也具有相对性,在不同的全集下,一个集合的补集可能不相同.
4.设U是全集,A是U的一个子集,那么对于U中的任何一个元素x,要么x∈A,要么x∈?UA.12【做一做1-1】 若集合U={1,2,3,4,5},A={2,4,5},则?UA等于( )
A.{2,4,5} B.{1,3}
C.{1,2,3} D.{1,2,3,4,5}
答案:B12【做一做1-2】 已知全集U=R,若集合M={x|-1≤x≤3},则?UM等于( )
A.{x|-1B.{x|-1≤x≤3}
C.{x|x<-1或x>3}
D.{x|x≤-1或x≥3}
解析:集合M的数轴表示如图所示,
由补集的定义,并结合数轴解题.
因为M={x|-1≤x≤3},
所以?UM={x|x<-1或x>3}.
答案:C122.补集的性质
对于任意集合A,有
A∪?UA=U,A∩?UA=?,?U(?UA)=A,?UU=?,?U?=U.
【做一做2-1】 已知全集U={x∈Z|-2 017解析:根据补集的性质?U(?UA)=A,可知?U(?UA)={0}.
答案:{0}12【做一做2-2】 有下列叙述:
①?UA={x|x?A};
②?U?=U;
③A∪?UA=?;
④若U={1,2,3},A={2,3,4},则?UA={1}.
其中正确的序号是 .?
解析:①应为?UA={x|x∈U,且x?A};
②正确;
③应为A∪?UA=U;
④因为A?U,所以?UA无意义.
答案:②一、子集A在全集U中的补集的求法
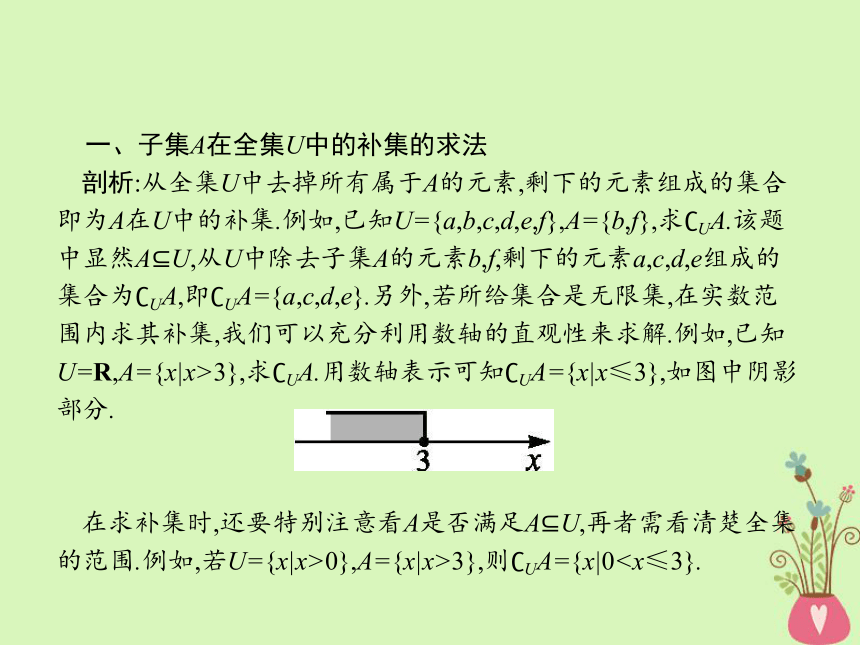
剖析:从全集U中去掉所有属于A的元素,剩下的元素组成的集合即为A在U中的补集.例如,已知U={a,b,c,d,e,f},A={b,f},求?UA.该题中显然A?U,从U中除去子集A的元素b,f,剩下的元素a,c,d,e组成的集合为?UA,即?UA={a,c,d,e}.另外,若所给集合是无限集,在实数范围内求其补集,我们可以充分利用数轴的直观性来求解.例如,已知U=R,A={x|x>3},求?UA.用数轴表示可知?UA={x|x≤3},如图中阴影部分.
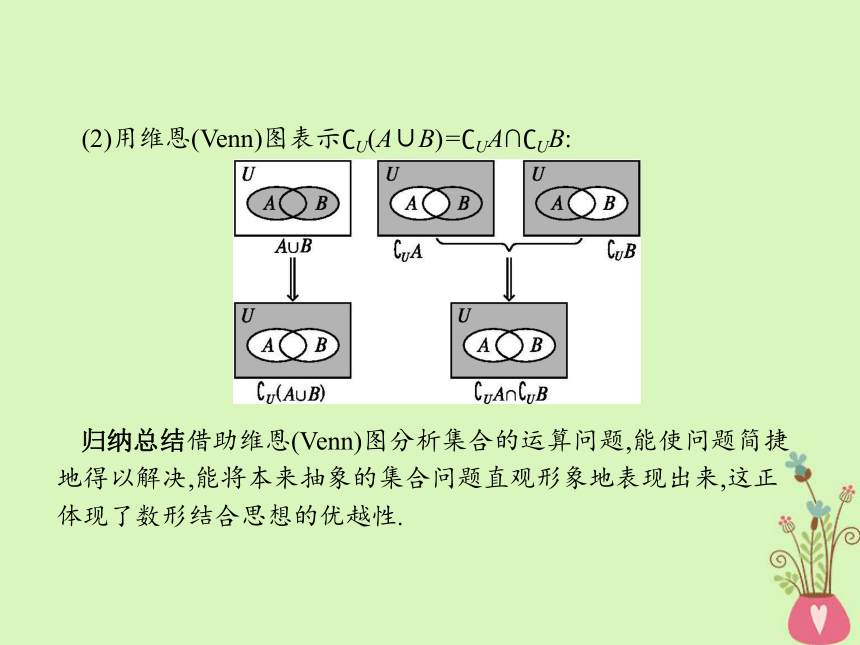
在求补集时,还要特别注意看A是否满足A?U,再者需看清楚全集的范围.例如,若U={x|x>0},A={x|x>3},则?UA={x|0剖析:(1)用维恩(Venn)图表示?U(A∩B)=?UA∪?UB:(2)用维恩(Venn)图表示?U(A∪B)=?UA∩?UB:
归纳总结借助维恩(Venn)图分析集合的运算问题,能使问题简捷地得以解决,能将本来抽象的集合问题直观形象地表现出来,这正体现了数形结合思想的优越性.题型一题型二题型三题型四【例1】 (1)已知全集U={三角形},集合A={直角三角形},求?UA;
(2)已知全集U={1,2,3,4,5,6,7,8,9},集合A={2,4,5},B={1,4,5},求?UA,?UA∪?UB;
(3)已知全集U={x|x≤4},集合A={x|-2≤x≤3},B={x|-3≤x≤2},求A∩?UB,?UA∪B,?UA∪?UB.
分析:这是一类涉及集合补集关系的运算,解题的关键是先明确全集,根据补集的定义求出集合的补集,再根据交集、并集的定义进行运算.题型一题型二题型三题型四解:(1)因为U={三角形},A={直角三角形},所以?UA={锐角三角形或钝角三角形}.
(2)因为全集U={1,2,3,4,5,6,7,8,9},集合A={2,4,5},所以?UA={1,3,6,7,8,9}.
又因为B={1,4,5},所以?UB={2,3,6,7,8,9}.
所以?UA∪?UB={1,2,3,6,7,8,9}.
(3)首先在数轴上表示出全集U和集合A,B(如图所示),
则?UA={x|x<-2或3(2)已知全集U={0,1,2,3,4,5,6},集合A满足?UA={0,1,3,5},求A;
(3)已知全集U=R,集合A={x|x≥4},B={x|-2解:(1)依题意可得?UM={奇数};
(2)因为?UA={0,1,3,5},所以A={2,4,6};
(3)由已知得?UB={x|x≤-2或x≥3},
所以A∩?UB={x|x≥4}.
又因为?UA={x|x<4},所以?UA∪B={x|x<4}.题型一题型二题型三题型四【例2】 设全集U={2,3,a2+2a-3},集合A={|a+1|,2},?UA={5},求a的值.
分析:由条件?UA={5},得5∈U,注意验证结果是否满足题意.
解:由?UA={5},知a2+2a-3=5,解得a=-4或a=2.
当a=-4时,U={2,3,5},A={3,2},满足条件?UA={5};
当a=2时,U={2,3,5},A={3,2},满足条件?UA={5}.
所以a的值为-4或2.
反思通过本题的解决,我们必须认识到找准解决问题的切入点是解题的关键,此题5∈U就是切入点,另外还要注意对A?U及?UA={5}的检验.题型一题型二题型三题型四【变式训练2】 已知集合A={x|x>a},B={x|1解析:因为B={x|1又A∪?RB=R,结合数轴分析,可得a≤1.
答案:a≤1题型一题型二题型三题型四【例3】 已知A={x|x2-2x-8=0},B={x|x2+ax+a2-12=0}.若B∪A≠A,求实数a的取值范围.
分析:B∪A≠A说明B不是A的子集,方程x2-2x-8=0的解为-2,4,则方程x2+ax+a2-12=0的实数解组成的集合可能出现以下几种情况:①-2是解,4不是解;②4是解,-2不是解;③-2和4都不是解.分别求解十分烦琐,这时我们先由B∪A=A,求出a的取值范围,再利用补集思想求解.题型一题型二题型三题型四解:若B∪A=A,则B?A.
因为A={x|x2-2x-8=0}={-2,4},
所以集合B有以下三种情况:
①当B=?时,Δ=a2-4(a2-12)<0,即a2>16,
所以a<-4或a>4.
②当B是单元素集时,Δ=a2-4(a2-12)=0,
所以a=-4或a=4.
若a=-4,则B={2}?A;若a=4,则B={-2}?A.
③当B={-2,4}时,-2,4是方程x2+ax+a2-12=0的两根,
综上可知,当B∪A=A时,a的取值范围为a<-4或a=-2或a≥4.
所以满足B∪A≠A的实数a的取值范围为{a|-4≤a<4,且a≠-2}.题型一题型二题型三题型四反思对于一些比较复杂、比较抽象、条件和结论之间的关系不明确、难以从正面入手的问题,在解题时,应及时调整思路,从问题的反面入手,探求已知和未知的关系,这样能化难为易,化隐为显,从而解决问题.题型一题型二题型三题型四【变式训练3】 已知集合P={x|2x3-x2+2ax-3a≥0},若-1?P,则实数a的取值范围是 .?题型一题型二题型三题型四题型一题型二题型三题型四
所以?UA={x|x≥1}.
由图可知,
当a<1时,?UA?B;
当a≥1时,?UA?B.
所以实数a的取值范围是{a|a<1}.
反思求某一集合的补集,首先应明确这一集合,最好不要急于对集合中的方程、不等式等进行对立面的转化,这样易出现转化不等价的情况,再就是要充分利用维恩(Venn)图或数轴表示集合来解决问题.题型一题型二题型三题型四答案:m≤2 1 2 3 4 5 61若集合U={1,2,3,4,5},A={1,2},B={2,3,4},则?U(A∪B)等于( )
A.{2} B.{5}
C.{1,2,3,4} D.{1,3,4,5}
解析:A∪B={1,2,3,4},则?U(A∪B)={5}.
答案:B1 2 3 4 5 62已知集合A={x∈R|-2A.{x|x<6} B.{x|-2C.{x|x>-2} D.{x|2≤x<6}
解析:由B={x∈R|x<2},
得?RB={x|x≥2}.
因为A={x∈R|-2所以A∪?RB={x|x>-2}.
答案:C1 2 3 4 5 63若集合A,B都是全集U的子集,给出下列命题:
①若A∩B=U,则A=B=U;
②若A∪B=?,则A=B=?;
③若A∪B=U,则?UA∩?UB=?;
④若A∩B=?,则A=B=?;
⑤若A∩B=?,则?UA∪?UB=U;
⑥若A∪B=U,则A=B=U.
其中不正确命题的个数是( )
A.0 B.2 C.4 D.61 2 3 4 5 6解析:①如果集合A,B中有一个为U的真子集,那么A∩B≠U,故A=B=U;②若集合A,B中有一个不为空集,则A∪B≠?,故A=B=?;③因为?UA∩?UB=?U(A∪B),而A∪B=U,所以?UA∩?UB=?U(A∪B)=?;④当集合A,B中只要有一个为空集或两个集合中没有共同的元素,就有A∩B=?,故不一定有A=B=?;⑤因为?UA∪?UB=?U(A∩B),而A∩B=?,所以?UA∪?UB=?U(A∩B)=U;⑥A∪B=U时,还有可能是A=?,B=U等情况,不一定有A=B=U.因此,不正确的为④⑥.
答案:B1 2 3 4 5 64若集合M={(x,y)|2x+3y>5a},且(-1,2)?M,则实数a的取值范围是 .?1 2 3 4 5 65设全集为U,用集合A,B的交集、并集、补集符号表示图中的阴影部分.
答案:(1)?U(A∪B) (2)?UA∩B1 2 3 4 5 66已知全集U={2,0,3-a2},U的子集P={2,a2-a-2},?UP={-1},求实数a的值.
分析:根据补集的定义及元素的互异性列出方程组,然后解得a的值.
2.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
3.重视补集思想在解题中的应用.121.全集与补集
如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示.
如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记作?UA,读作“A在U中的补集”.12归纳总结1.补集的符号语言为:?UA={x|x∈U,且x?A};
2.补集的维恩(Venn)图表示如图所示;
3.全集具有相对性,即研究某个问题时的全集可能在研究另一个问题时就不是全集.补集是相对于全集而言的,由于全集具有相对性,那么补集也具有相对性,在不同的全集下,一个集合的补集可能不相同.
4.设U是全集,A是U的一个子集,那么对于U中的任何一个元素x,要么x∈A,要么x∈?UA.12【做一做1-1】 若集合U={1,2,3,4,5},A={2,4,5},则?UA等于( )
A.{2,4,5} B.{1,3}
C.{1,2,3} D.{1,2,3,4,5}
答案:B12【做一做1-2】 已知全集U=R,若集合M={x|-1≤x≤3},则?UM等于( )
A.{x|-1
C.{x|x<-1或x>3}
D.{x|x≤-1或x≥3}
解析:集合M的数轴表示如图所示,
由补集的定义,并结合数轴解题.
因为M={x|-1≤x≤3},
所以?UM={x|x<-1或x>3}.
答案:C122.补集的性质
对于任意集合A,有
A∪?UA=U,A∩?UA=?,?U(?UA)=A,?UU=?,?U?=U.
【做一做2-1】 已知全集U={x∈Z|-2 017
答案:{0}12【做一做2-2】 有下列叙述:
①?UA={x|x?A};
②?U?=U;
③A∪?UA=?;
④若U={1,2,3},A={2,3,4},则?UA={1}.
其中正确的序号是 .?
解析:①应为?UA={x|x∈U,且x?A};
②正确;
③应为A∪?UA=U;
④因为A?U,所以?UA无意义.
答案:②一、子集A在全集U中的补集的求法
剖析:从全集U中去掉所有属于A的元素,剩下的元素组成的集合即为A在U中的补集.例如,已知U={a,b,c,d,e,f},A={b,f},求?UA.该题中显然A?U,从U中除去子集A的元素b,f,剩下的元素a,c,d,e组成的集合为?UA,即?UA={a,c,d,e}.另外,若所给集合是无限集,在实数范围内求其补集,我们可以充分利用数轴的直观性来求解.例如,已知U=R,A={x|x>3},求?UA.用数轴表示可知?UA={x|x≤3},如图中阴影部分.
在求补集时,还要特别注意看A是否满足A?U,再者需看清楚全集的范围.例如,若U={x|x>0},A={x|x>3},则?UA={x|0
归纳总结借助维恩(Venn)图分析集合的运算问题,能使问题简捷地得以解决,能将本来抽象的集合问题直观形象地表现出来,这正体现了数形结合思想的优越性.题型一题型二题型三题型四【例1】 (1)已知全集U={三角形},集合A={直角三角形},求?UA;
(2)已知全集U={1,2,3,4,5,6,7,8,9},集合A={2,4,5},B={1,4,5},求?UA,?UA∪?UB;
(3)已知全集U={x|x≤4},集合A={x|-2≤x≤3},B={x|-3≤x≤2},求A∩?UB,?UA∪B,?UA∪?UB.
分析:这是一类涉及集合补集关系的运算,解题的关键是先明确全集,根据补集的定义求出集合的补集,再根据交集、并集的定义进行运算.题型一题型二题型三题型四解:(1)因为U={三角形},A={直角三角形},所以?UA={锐角三角形或钝角三角形}.
(2)因为全集U={1,2,3,4,5,6,7,8,9},集合A={2,4,5},所以?UA={1,3,6,7,8,9}.
又因为B={1,4,5},所以?UB={2,3,6,7,8,9}.
所以?UA∪?UB={1,2,3,6,7,8,9}.
(3)首先在数轴上表示出全集U和集合A,B(如图所示),
则?UA={x|x<-2或3
(3)已知全集U=R,集合A={x|x≥4},B={x|-2
(2)因为?UA={0,1,3,5},所以A={2,4,6};
(3)由已知得?UB={x|x≤-2或x≥3},
所以A∩?UB={x|x≥4}.
又因为?UA={x|x<4},所以?UA∪B={x|x<4}.题型一题型二题型三题型四【例2】 设全集U={2,3,a2+2a-3},集合A={|a+1|,2},?UA={5},求a的值.
分析:由条件?UA={5},得5∈U,注意验证结果是否满足题意.
解:由?UA={5},知a2+2a-3=5,解得a=-4或a=2.
当a=-4时,U={2,3,5},A={3,2},满足条件?UA={5};
当a=2时,U={2,3,5},A={3,2},满足条件?UA={5}.
所以a的值为-4或2.
反思通过本题的解决,我们必须认识到找准解决问题的切入点是解题的关键,此题5∈U就是切入点,另外还要注意对A?U及?UA={5}的检验.题型一题型二题型三题型四【变式训练2】 已知集合A={x|x>a},B={x|1
答案:a≤1题型一题型二题型三题型四【例3】 已知A={x|x2-2x-8=0},B={x|x2+ax+a2-12=0}.若B∪A≠A,求实数a的取值范围.
分析:B∪A≠A说明B不是A的子集,方程x2-2x-8=0的解为-2,4,则方程x2+ax+a2-12=0的实数解组成的集合可能出现以下几种情况:①-2是解,4不是解;②4是解,-2不是解;③-2和4都不是解.分别求解十分烦琐,这时我们先由B∪A=A,求出a的取值范围,再利用补集思想求解.题型一题型二题型三题型四解:若B∪A=A,则B?A.
因为A={x|x2-2x-8=0}={-2,4},
所以集合B有以下三种情况:
①当B=?时,Δ=a2-4(a2-12)<0,即a2>16,
所以a<-4或a>4.
②当B是单元素集时,Δ=a2-4(a2-12)=0,
所以a=-4或a=4.
若a=-4,则B={2}?A;若a=4,则B={-2}?A.
③当B={-2,4}时,-2,4是方程x2+ax+a2-12=0的两根,
综上可知,当B∪A=A时,a的取值范围为a<-4或a=-2或a≥4.
所以满足B∪A≠A的实数a的取值范围为{a|-4≤a<4,且a≠-2}.题型一题型二题型三题型四反思对于一些比较复杂、比较抽象、条件和结论之间的关系不明确、难以从正面入手的问题,在解题时,应及时调整思路,从问题的反面入手,探求已知和未知的关系,这样能化难为易,化隐为显,从而解决问题.题型一题型二题型三题型四【变式训练3】 已知集合P={x|2x3-x2+2ax-3a≥0},若-1?P,则实数a的取值范围是 .?题型一题型二题型三题型四题型一题型二题型三题型四
所以?UA={x|x≥1}.
由图可知,
当a<1时,?UA?B;
当a≥1时,?UA?B.
所以实数a的取值范围是{a|a<1}.
反思求某一集合的补集,首先应明确这一集合,最好不要急于对集合中的方程、不等式等进行对立面的转化,这样易出现转化不等价的情况,再就是要充分利用维恩(Venn)图或数轴表示集合来解决问题.题型一题型二题型三题型四答案:m≤2 1 2 3 4 5 61若集合U={1,2,3,4,5},A={1,2},B={2,3,4},则?U(A∪B)等于( )
A.{2} B.{5}
C.{1,2,3,4} D.{1,3,4,5}
解析:A∪B={1,2,3,4},则?U(A∪B)={5}.
答案:B1 2 3 4 5 62已知集合A={x∈R|-2
解析:由B={x∈R|x<2},
得?RB={x|x≥2}.
因为A={x∈R|-2
答案:C1 2 3 4 5 63若集合A,B都是全集U的子集,给出下列命题:
①若A∩B=U,则A=B=U;
②若A∪B=?,则A=B=?;
③若A∪B=U,则?UA∩?UB=?;
④若A∩B=?,则A=B=?;
⑤若A∩B=?,则?UA∪?UB=U;
⑥若A∪B=U,则A=B=U.
其中不正确命题的个数是( )
A.0 B.2 C.4 D.61 2 3 4 5 6解析:①如果集合A,B中有一个为U的真子集,那么A∩B≠U,故A=B=U;②若集合A,B中有一个不为空集,则A∪B≠?,故A=B=?;③因为?UA∩?UB=?U(A∪B),而A∪B=U,所以?UA∩?UB=?U(A∪B)=?;④当集合A,B中只要有一个为空集或两个集合中没有共同的元素,就有A∩B=?,故不一定有A=B=?;⑤因为?UA∪?UB=?U(A∩B),而A∩B=?,所以?UA∪?UB=?U(A∩B)=U;⑥A∪B=U时,还有可能是A=?,B=U等情况,不一定有A=B=U.因此,不正确的为④⑥.
答案:B1 2 3 4 5 64若集合M={(x,y)|2x+3y>5a},且(-1,2)?M,则实数a的取值范围是 .?1 2 3 4 5 65设全集为U,用集合A,B的交集、并集、补集符号表示图中的阴影部分.
答案:(1)?U(A∪B) (2)?UA∩B1 2 3 4 5 66已知全集U={2,0,3-a2},U的子集P={2,a2-a-2},?UP={-1},求实数a的值.
分析:根据补集的定义及元素的互异性列出方程组,然后解得a的值.
