2019-2020学年高中数学新人教B版必修1课件:第3章基本初等函数3.2.2对数函数(47张)
文档属性
| 名称 | 2019-2020学年高中数学新人教B版必修1课件:第3章基本初等函数3.2.2对数函数(47张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览











文档简介
课件47张PPT。3.2.2 对数函数1.理解对数函数的概念,体会对数函数是一类重要的函数模型.
2.能借助计算器或计算机画出具体对数函数的图象.
3.通过具体实例,直观了解对数函数模型所刻画的数量关系.
4.熟练掌握对数函数的图象和性质.121.对数函数的定义
函数y=logax(a>0,a≠1,x>0)称为对数函数,其中x是自变量.
名师点拨1.对数函数也采取形式化的定义方式,即形如y=logax(a>0,a≠1,x>0)的函数叫做对数函数.对数函数的解析式具有以下特征:对数符号前面的系数等于1;对数的底数必须是大于0且不等于1的实数;对数的真数仅为自变量x.
2.对数函数的解析式中其底数与指数函数解析式中的底数在范围上是一样的,即a>0,且a≠1.
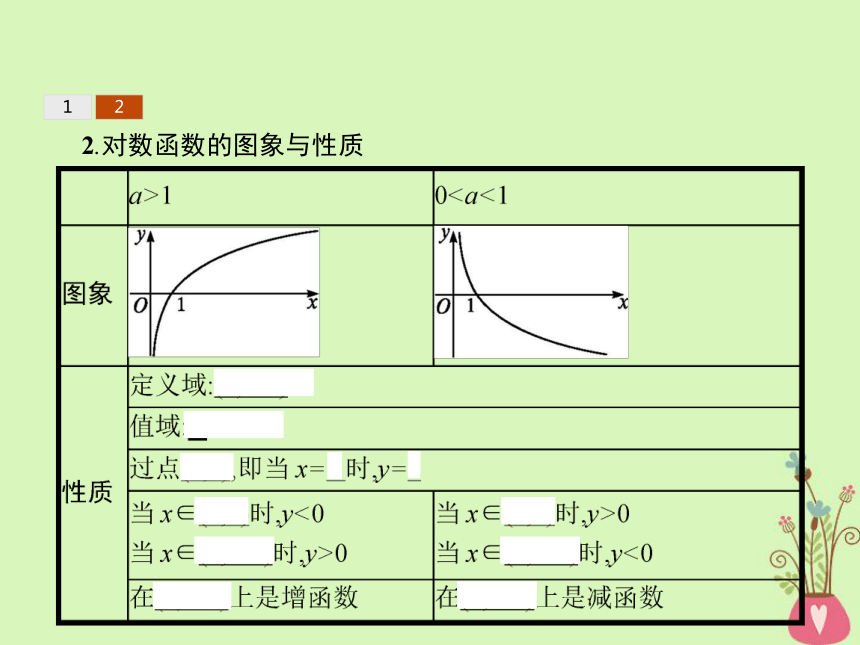
3.由对数函数的定义可知,对数函数与指数函数的定义域和值域恰好互换.12答案:② 122.对数函数的图象与性质 12归纳总结1.对数函数的图象都经过定点(1,0)是因为不论a取何值,总有loga1=0.对于函数y=logaf(x)+b(a>0,a≠1),若令f(x)=1,解得x=x0,则该函数图象一定经过定点(x0,b).
3.设y1=logax,y2=logbx,其中a>1,b>1(或0当x>1时,“底大图低”,即若a>b,则y1当0b,则y1>y2.
4.对于对数函数y=logax,当y=1时,x=a,而a恰好又是对数函数的底数,这就启发我们,不妨作直线y=1,它与对数函数的图象相交,交点的横坐标恰好就是对数函数的底数,用这种办法可以快速地比较出多个对数函数的底数的大小.12【做一做2-1】 下列函数中,在区间(0,+∞)上不是增函数的是( )
A.y=5x B.y=lg x+2
答案:D12【做一做2-2】 函数f(x)=|log2x|的图象是( )
答案:A12【做一做2-3】 若a>0,且a≠1,则函数y=loga(x-1)-1的图象恒过点 .?
解析:由函数y=logax的图象恒过点(1,0)可知,
当x-1=1,即x=2时,y=-1.
答案:(2,-1)一、底数对对数函数图象的影响
剖析:在同一平面直角坐标系中分别作出函数y=log2x及y=log3x的图象,如图所示,可以看出,底数越大,图象越靠近x轴.同理,当01)及y=logax(0剖析:利用对数函数的性质可以比较两个对数的大小,常用的方法是:当底数相同真数不相同时,直接利用对数函数的单调性进行比较,即当a>1时,在(0,+∞)上是增函数,当0对于多个对数的大小比较,通常先找出(-∞,0),(0,1),(1,+∞)中的各数,然后把位于同一区间中的数进行比较.三、函数y=|logax|(a>0,a≠1)与y=loga|x|(a>0,a≠1)的图象与性质
剖析:(1)函数y=|logax|(a>0,a≠1)的图象与性质(2)函数y=loga|x|(a>0,a≠1)的图象与性质 四、教材中的“?”
对数函数y=logax(a>0,且a≠1),当a>1,x取何值时,y>0?x取何值时,y<0?0剖析:结合对数函数的图象可知,
当a>1时,若x>1,则y>0;若0当01,则y<0;若00.
实际上,观察对数函数的图象不难发现,对数函数中的值y=logmn有以下规律:
(1)当(m-1)(n-1)>0,即m,n的取值范围相同(相对于“1”而言)时,logmn>0;
(2)当(m-1)(n-1)<0,即m,n的取值范围相反(相对于“1”而言)时,logmn<0.有了以上规律,我们再判断对数值的正负就很简单了.题型一题型二题型三题型四题型五分析:按照求函数定义域的基本要求以及对数式中“真数大于0”这一限制条件,列不等式组求解.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思根据解析式,求与对数有关的函数的定义域,除了我们以前知道的限制条件外,还要注意对数的底数大于0不等于1,真数大于0.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例2】 求函数y=log2(x2+2x+5)的值域.
分析:先对真数配方,再利用对数函数的单调性求解.
解:因为函数的定义域为R,
且x2+2x+5=(x+1)2+4≥4>0,
所以log2(x2+2x+5)≥log24=2,
即函数的值域为[2,+∞).
反思求与对数函数相关的函数的值域时,首先应确定其定义域,然后求出真数上的代数式的取值范围,再结合对数函数的单调性求出其值域.题型一题型二题型三题型四题型五【变式训练2】 求下列函数的值域:
(1)f(x)=log3(2x-1),x∈[2,14];
解:(1)当2≤x≤14时,3≤2x-1≤27,
故1≤log3(2x-1)≤3,
即函数的值域为[1,3].
(2)因为3+2x-x2=-x2+2x-1+4=-(x-1)2+4≤4,
故函数的值域为[-2,+∞).题型一题型二题型三题型四题型五【例3】 比较大小:
(1)log0.27与log0.29;
(2)(lg m)1.9与(lg m)2.1(m>1);
(3)log85与lg 4.题型一题型二题型三题型四题型五解:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两个函数值,由y=log0.2x在(0,+∞)上单调递减,得log0.27>log0.29.
(2)把lg m看作指数函数y=ax(a>0,且a≠1)的底数,要比较两数的大小,关键是比较底数lg m与1的关系.
若lg m>1,即m>10,则y=(lg m)x在R上单调递增,故(lg m)1.9<(lg m)2.1;若0(lg m)2.1;若lg m=1,即m=10,则(lg m)1.9=(lg m)2.1.
(3)因为底数8,10均大于1,且10>8,
所以log85>lg 5>lg 4,即log85>lg 4.题型一题型二题型三题型四题型五反思本例中(1)小题是直接利用对数函数的单调性;(2)小题是指数函数单调性及对数函数性质的综合运用;(3)小题是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的单调性求解.常用的中间量有0,1,2等,可通过估算加以选择.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例4】 画出函数y=log2x2的图象,并根据图象指出它的单调区间.
分析:先对函数的定义域及奇偶性进行探索,再画图象研究函数的单调区间.题型一题型二题型三题型四题型五解:由题意知,函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.
因为f(-x)=log2(-x)2=log2x2=f(x),
所以y=log2x2是偶函数,它的图象关于y轴对称.
当x>0时,y=log2x2=2log2x,因此先画出
y=2log2x(x>0)的图象为C1,再作出C1关于y轴对
称的图象C2,C1与C2构成函数y=log2x2的图象,如图所示.
由图象可以知道函数y=log2x2的单调递减区间是(-∞,0),单调递增区间是(0,+∞).
反思作图象时一定要考虑函数的定义域,否则会求出错误的单调区间.同时在确定单调区间时,要注意单调区间的分界点,特别要注意区间的开与闭.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例5】 画出函数y=|log2(x+1)|+2的图象.
分析:可先画出它的基本函数的图象,再做适当的变换,然后分步骤完成.
解:第一步:作y=log2x的图象,如图①所示.
第二步:将y=log2x的图象沿x轴向左平移1个单位,得y=log2(x+1)的图象,如图②所示.
第三步:将y=log2(x+1)在x轴下方的图象作关于x轴的对称变换,得y=|log2(x+1)|的图象,如图③所示.
第四步:将y=|log2(x+1)|的图象沿y轴方向向上平移2个单位,便得到所求函数y=|log2(x+1)|+2的图象,如图④所示.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思含有绝对值的函数的图象可通过对称变换得到,一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象,在f(x)≥0时相同,而在f(x)<0时,关于x轴对称.题型一题型二题型三题型四题型五答案:D 题型一题型二题型三题型四题型五【例6】 已知函数f(x)=log2(3x2-2x-1),试确定f(x)的单调递增区间.
分析:根据复合函数单调性的知识可知,要使f(x)为增函数,则内、外层函数的单调性一致.因为2>1,所以y=log2x为增函数,故只需求函数y=3x2-2x-1的单调递增区间即可,但不能忽略函数的定义域.题型一题型二题型三题型四题型五反思求复合函数的单调区间的步骤:(1)求出函数的定义域;(2)将复合函数分解为初等函数;(3)分别确定各个初等函数的单调性;(4)根据复合函数原理求出复合函数的单调区间.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五错因分析:错解一中没考虑真数的取值范围,也没有对a进行分类讨论;错解二中没有对a进行分类讨论;错解三中出现逻辑性错误,运算变形的顺序出现了问题,即开始默认了a>1对原不等式进行了转化是不正确的,虽然后来对a又进行了讨论,看起来结果正确.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思平时同学们做题难免出错,但要查找原因,从错误中汲取经验,才能对知识的理解更加完善.题型一题型二题型三题型四题型五1 2 3 4 5 6答案:B 1 2 3 4 5 62设a=log3π,b=log76,c=log20.8,则( )
A.a>b>c B.b>a>c C.c>a>b D.b>c>a
解析:a=log3π>log33=1;b=log76b>c.
答案:A1 2 3 4 5 63设0A.0C.0答案:B1 2 3 4 5 6解析:当a>1时,图象上升;01时,a越大,图象向右越靠近于x轴;当0答案:A1 2 3 4 5 65函数f(x)=loga(4x-7)-3(a>0,a≠1)的图象一定经过定点 .?
解析:不论a取何值,总有f(2)=loga1-3=-3,即图象一定经过点(2,-3).
答案:(2,-3)1 2 3 4 5 6
2.能借助计算器或计算机画出具体对数函数的图象.
3.通过具体实例,直观了解对数函数模型所刻画的数量关系.
4.熟练掌握对数函数的图象和性质.121.对数函数的定义
函数y=logax(a>0,a≠1,x>0)称为对数函数,其中x是自变量.
名师点拨1.对数函数也采取形式化的定义方式,即形如y=logax(a>0,a≠1,x>0)的函数叫做对数函数.对数函数的解析式具有以下特征:对数符号前面的系数等于1;对数的底数必须是大于0且不等于1的实数;对数的真数仅为自变量x.
2.对数函数的解析式中其底数与指数函数解析式中的底数在范围上是一样的,即a>0,且a≠1.
3.由对数函数的定义可知,对数函数与指数函数的定义域和值域恰好互换.12答案:② 122.对数函数的图象与性质 12归纳总结1.对数函数的图象都经过定点(1,0)是因为不论a取何值,总有loga1=0.对于函数y=logaf(x)+b(a>0,a≠1),若令f(x)=1,解得x=x0,则该函数图象一定经过定点(x0,b).
3.设y1=logax,y2=logbx,其中a>1,b>1(或0
4.对于对数函数y=logax,当y=1时,x=a,而a恰好又是对数函数的底数,这就启发我们,不妨作直线y=1,它与对数函数的图象相交,交点的横坐标恰好就是对数函数的底数,用这种办法可以快速地比较出多个对数函数的底数的大小.12【做一做2-1】 下列函数中,在区间(0,+∞)上不是增函数的是( )
A.y=5x B.y=lg x+2
答案:D12【做一做2-2】 函数f(x)=|log2x|的图象是( )
答案:A12【做一做2-3】 若a>0,且a≠1,则函数y=loga(x-1)-1的图象恒过点 .?
解析:由函数y=logax的图象恒过点(1,0)可知,
当x-1=1,即x=2时,y=-1.
答案:(2,-1)一、底数对对数函数图象的影响
剖析:在同一平面直角坐标系中分别作出函数y=log2x及y=log3x的图象,如图所示,可以看出,底数越大,图象越靠近x轴.同理,当0
剖析:(1)函数y=|logax|(a>0,a≠1)的图象与性质(2)函数y=loga|x|(a>0,a≠1)的图象与性质 四、教材中的“?”
对数函数y=logax(a>0,且a≠1),当a>1,x取何值时,y>0?x取何值时,y<0?0
当a>1时,若x>1,则y>0;若0
实际上,观察对数函数的图象不难发现,对数函数中的值y=logmn有以下规律:
(1)当(m-1)(n-1)>0,即m,n的取值范围相同(相对于“1”而言)时,logmn>0;
(2)当(m-1)(n-1)<0,即m,n的取值范围相反(相对于“1”而言)时,logmn<0.有了以上规律,我们再判断对数值的正负就很简单了.题型一题型二题型三题型四题型五分析:按照求函数定义域的基本要求以及对数式中“真数大于0”这一限制条件,列不等式组求解.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思根据解析式,求与对数有关的函数的定义域,除了我们以前知道的限制条件外,还要注意对数的底数大于0不等于1,真数大于0.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例2】 求函数y=log2(x2+2x+5)的值域.
分析:先对真数配方,再利用对数函数的单调性求解.
解:因为函数的定义域为R,
且x2+2x+5=(x+1)2+4≥4>0,
所以log2(x2+2x+5)≥log24=2,
即函数的值域为[2,+∞).
反思求与对数函数相关的函数的值域时,首先应确定其定义域,然后求出真数上的代数式的取值范围,再结合对数函数的单调性求出其值域.题型一题型二题型三题型四题型五【变式训练2】 求下列函数的值域:
(1)f(x)=log3(2x-1),x∈[2,14];
解:(1)当2≤x≤14时,3≤2x-1≤27,
故1≤log3(2x-1)≤3,
即函数的值域为[1,3].
(2)因为3+2x-x2=-x2+2x-1+4=-(x-1)2+4≤4,
故函数的值域为[-2,+∞).题型一题型二题型三题型四题型五【例3】 比较大小:
(1)log0.27与log0.29;
(2)(lg m)1.9与(lg m)2.1(m>1);
(3)log85与lg 4.题型一题型二题型三题型四题型五解:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两个函数值,由y=log0.2x在(0,+∞)上单调递减,得log0.27>log0.29.
(2)把lg m看作指数函数y=ax(a>0,且a≠1)的底数,要比较两数的大小,关键是比较底数lg m与1的关系.
若lg m>1,即m>10,则y=(lg m)x在R上单调递增,故(lg m)1.9<(lg m)2.1;若0
(3)因为底数8,10均大于1,且10>8,
所以log85>lg 5>lg 4,即log85>lg 4.题型一题型二题型三题型四题型五反思本例中(1)小题是直接利用对数函数的单调性;(2)小题是指数函数单调性及对数函数性质的综合运用;(3)小题是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的单调性求解.常用的中间量有0,1,2等,可通过估算加以选择.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例4】 画出函数y=log2x2的图象,并根据图象指出它的单调区间.
分析:先对函数的定义域及奇偶性进行探索,再画图象研究函数的单调区间.题型一题型二题型三题型四题型五解:由题意知,函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.
因为f(-x)=log2(-x)2=log2x2=f(x),
所以y=log2x2是偶函数,它的图象关于y轴对称.
当x>0时,y=log2x2=2log2x,因此先画出
y=2log2x(x>0)的图象为C1,再作出C1关于y轴对
称的图象C2,C1与C2构成函数y=log2x2的图象,如图所示.
由图象可以知道函数y=log2x2的单调递减区间是(-∞,0),单调递增区间是(0,+∞).
反思作图象时一定要考虑函数的定义域,否则会求出错误的单调区间.同时在确定单调区间时,要注意单调区间的分界点,特别要注意区间的开与闭.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五【例5】 画出函数y=|log2(x+1)|+2的图象.
分析:可先画出它的基本函数的图象,再做适当的变换,然后分步骤完成.
解:第一步:作y=log2x的图象,如图①所示.
第二步:将y=log2x的图象沿x轴向左平移1个单位,得y=log2(x+1)的图象,如图②所示.
第三步:将y=log2(x+1)在x轴下方的图象作关于x轴的对称变换,得y=|log2(x+1)|的图象,如图③所示.
第四步:将y=|log2(x+1)|的图象沿y轴方向向上平移2个单位,便得到所求函数y=|log2(x+1)|+2的图象,如图④所示.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思含有绝对值的函数的图象可通过对称变换得到,一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象,在f(x)≥0时相同,而在f(x)<0时,关于x轴对称.题型一题型二题型三题型四题型五答案:D 题型一题型二题型三题型四题型五【例6】 已知函数f(x)=log2(3x2-2x-1),试确定f(x)的单调递增区间.
分析:根据复合函数单调性的知识可知,要使f(x)为增函数,则内、外层函数的单调性一致.因为2>1,所以y=log2x为增函数,故只需求函数y=3x2-2x-1的单调递增区间即可,但不能忽略函数的定义域.题型一题型二题型三题型四题型五反思求复合函数的单调区间的步骤:(1)求出函数的定义域;(2)将复合函数分解为初等函数;(3)分别确定各个初等函数的单调性;(4)根据复合函数原理求出复合函数的单调区间.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五错因分析:错解一中没考虑真数的取值范围,也没有对a进行分类讨论;错解二中没有对a进行分类讨论;错解三中出现逻辑性错误,运算变形的顺序出现了问题,即开始默认了a>1对原不等式进行了转化是不正确的,虽然后来对a又进行了讨论,看起来结果正确.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五反思平时同学们做题难免出错,但要查找原因,从错误中汲取经验,才能对知识的理解更加完善.题型一题型二题型三题型四题型五1 2 3 4 5 6答案:B 1 2 3 4 5 62设a=log3π,b=log76,c=log20.8,则( )
A.a>b>c B.b>a>c C.c>a>b D.b>c>a
解析:a=log3π>log33=1;b=log76
答案:A1 2 3 4 5 63设0
解析:不论a取何值,总有f(2)=loga1-3=-3,即图象一定经过点(2,-3).
答案:(2,-3)1 2 3 4 5 6
