2019-2020学年高中数学新人教B版必修1课件:第3章基本初等函数本章整合(41张)
文档属性
| 名称 | 2019-2020学年高中数学新人教B版必修1课件:第3章基本初等函数本章整合(41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 10:45:31 | ||
图片预览










文档简介
课件41张PPT。本章整合专题一专题二专题三专题四专题一 指数与对数的运算问题
指数与对数的运算是指数、对数应用的前提,也是研究指数函数与对数函数的基础,不仅是本章考查的重点,也是高考的重要考点之一.
进行指数式的运算时,要注意运算或化简的先后顺序,一般应将负指数转化为正指数、将根式转化为指数式后再计算或化简,同时注意幂的运算性质的应用;对数运算要注意对数运算性质的正用与逆用,注意对底数的转化,对数恒等式以及换底公式的灵活运用,还要注意对数运算与指数运算之间的关系及其合理地转化.专题一专题二专题三专题四专题一专题二专题三专题四?专题一专题二专题三专题四(3)原式=2log32-5log32+2+3log32-5
=2-5=-3.专题一专题二专题三专题四专题一专题二专题三专题四专题二 指数函数、对数函数、幂函数的图象和性质的应用
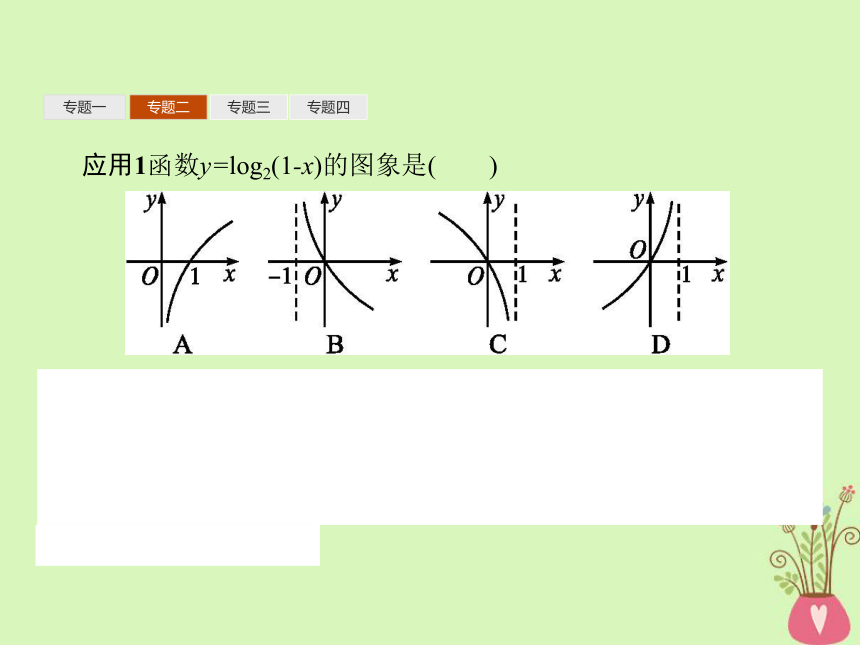
指数函数、对数函数、幂函数是重要的基本初等函数.它们的图象与性质始终是高考考查的重点.由于指数函数y=ax(a>0,a≠1,x∈R),对数函数y=logax(a>0,a≠1,x>0)的图象与性质都与a的取值有密切的联系,幂函数y=xα的图象与性质与α的取值有关,因此,在a,α的值不确定时,要对它们进行分类讨论,利用图象可以很快捷、直观地解决比较大小、求根等计算问题.专题一专题二专题三专题四应用1函数y=log2(1-x)的图象是( )
解析:由1-x>0得x<1,故函数定义域为(-∞,1),因此排除选项A,B;
又因为t=1-x在(-∞,1)上是单调递减的,
所以y=log2(1-x)在(-∞,1)上是减函数,由此排除D.
答案:C专题一专题二专题三专题四专题一专题二专题三专题四答案:D 专题一专题二专题三专题四应用3方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
解析:设y1=log3x,y2=-x+3,在同一平面直角坐标系中画出它们的图象如图所示,观察可排除选项A,D.故交点P的横坐标应在区间(1,3)内.
因为当x=2时,y1=log32<1,y2=-2+3=1,且y1是增函数,y2是减函数,
所以交点P的横坐标应在区间(2,3)内.
答案:C专题一专题二专题三专题四应用4若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上单调递减,则a的取值范围为( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)
答案:A专题一专题二专题三专题四专题一专题二专题三专题四专题三 分类讨论思想的应用
分类讨论思想即对问题中的参数不能一概而论,需要按一定的标准进行分别阐述,在分类讨论中要做到“不重复,不遗漏”.专题一专题二专题三专题四提示:将对数不等式统一成同底的形式,再利用分类讨论思想及函数的单调性进行转化求解.专题一专题二专题三专题四提示:按零点分类讨论法即把整个实数集R以±1为分界点分成(-∞,-1],(-1,1),[1,+∞)三段讨论.专题一专题二专题三专题四专题四 函数图象的平移、对称变换
图象变换题因其集数形结合的数学思想、运动变化的观点于一体,又考查了函数图象的画法和相关函数的性质,对于知识的内化、数学能力的提升均起到促进的作用,故在教材乃至高考试题中均占有重要的地位,不容忽视.下面总结一些常见的图象变换规律,供同学们参考.专题一专题二专题三专题四1.图象的平移变换
(1)水平平移:函数y=f(x±a)(a>0)的图象,可由y=f(x)的图象向左(+)或向右(-)平移a个单位长度而得到.
例如,将对数函数y=log2x的图象向左平移2个单位长度,便得到函数y=log2(x+2)的图象.
(2)竖直平移:函数y=f(x)±b(b>0)的图象,可由y=f(x)的图象向上(+)或向下(-)平移b个单位长度而得到.
例如,将指数函数y=x3的图象向下平移1个单位长度,便得到函数y=x3-1的图象.专题一专题二专题三专题四2.图象的对称变换
(1)y=f(-x)与y=f(x)的图象关于y轴对称.
(2)y=-f(x)与y=f(x)的图象关于x轴对称.
(3)y=-f(-x)与y=f(x)的图象关于原点对称.
(4)y=f-1(x)与y=f(x)的图象关于直线y=x对称.
例如,对数函数y=log2x的图象与指数函数y=2x的图象关于直线y=x对称.专题一专题二专题三专题四专题一专题二专题三专题四应用1画出函数y=log4(x2-2x+1)的图象.
提示:先要找出这个函数所对应的基本初等函数,然后利用图象变换向目标靠拢.
解:先对函数解析式进行化简,可得y=log2|x-1|.可直接利用描点法画出y=log2x的图象,而后画出关于y轴的对称变换得到y=log2|x|,再把其向右平移一个单位长度.过程如下:专题一专题二专题三专题四应用2(1)画出函数y=log2(x+2)与y=log2(x-2)的图象,并指出两个图象之间的关系;
(2)画出函数y=f(x)=log2|x|的图象,并根据图象指出它的单调区间.
提示:画函数图象是研究函数变化规律的重要手段,可利用y=log2x的图象进行变换.专题一专题二专题三专题四解:(1)函数y=log2x的图象向右平移2个单位长度就得到y=log2(x-2)的图象;向左平移2个单位长度就得到y=log2(x+2)的图象,
故把y=log2(x+2)的图象向右平移4个单位长度得到y=log2(x-2)的图象(如图所示).专题一专题二专题三专题四(2)当x≠0时,函数y=log2|x|满足f(-x)=log2|-x|=log2|x|=f(x),故y=log2|x|是偶函数,它的图象关于y轴对称.当x>0时,y=log2x.先画出y=log2x(x>0)的图象为C1,再作出C1关于y轴对称的图象C2,C1与C2构成函数y=log2|x|的图象,如图所示.
由图象可知,函数y=log2|x|的单调递减区间是(-∞,0),单调递增区间是(0,+∞).1 2 3 4 5 6 7 8 9 10 11 12
∴x>2,∴f(x)的定义域为(2,+∞).
答案:C1 2 3 4 5 6 7 8 9 10 11 122(北京高考)下列函数中,定义域是R且为增函数的是 ( )
A.y=e-x B.y=x3
C.y=ln x D.y=|x|
解析:A项,函数y=e-x为R上的减函数;
B项,函数y=x3为R上的增函数;
C项,函数y=ln x为(0,+∞)上的增函数;
D项,函数y=|x|在(-∞,0]上为减函数,在(0,+∞)上为增函数.故只有B项符合题意,应选B.
答案:B1 2 3 4 5 6 7 8 9 10 11 12的区间是( )
A.(0,1) B.(1,2)
C.(2,4) D.(4,+∞)答案:C 1 2 3 4 5 6 7 8 9 10 11 124(安徽高考)设a=log37,b=21.1,c=0.83.1,则( )
A.bC.c解析:∵log33∵21.1>21,∴b>2.
∵0<0.83.1<0.80,∴0答案:B1 2 3 4 5 6 7 8 9 10 11 125(山东高考)已知函数y=loga(x+c)(a,c为常数,其中a>0,a≠0)的图象如图,则下列结论成立的是( )
A.a>1,c>1
B.a>1,0C.01
D.0解析:由图象可知y=loga(x+c)的图象是由y=logax的图象向左平移c个单位长度得到的,其中0答案:D1 2 3 4 5 6 7 8 9 10 11 126(浙江高考)在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )1 2 3 4 5 6 7 8 9 10 11 12解析:若a>1,则函数g(x)=logax的图象过点(1,0),且单调递增,但当x∈(0,1)时,y=xa(x>0)的图象应在直线y=x的下方,故C选项错误.
若00)的图象应单调递增,且当x∈(0,1)时图象应在直线y=x的上方,因此A,B均错,只有D项正确.
答案:D1 2 3 4 5 6 7 8 9 10 11 127(福建高考)若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )1 2 3 4 5 6 7 8 9 10 11 12?1 2 3 4 5 6 7 8 9 10 11 12答案:D 1 2 3 4 5 6 7 8 9 10 11 121 2 3 4 5 6 7 8 9 10 11 12答案:1 1 2 3 4 5 6 7 8 9 10 11 12答案:(-∞,8]1 2 3 4 5 6 7 8 9 10 11 1212(天津高考)函数f(x)=lg x2的单调递减区间是 .?
解析:函数f(x)=lg x2的定义域为(-∞,0)∪(0,+∞).
∵f(x)=lg x在(0,+∞)上为增函数,y=x2在[0,+∞)上为增函数,在(-∞,0]上为减函数,
∴f(x)=lg x2的单调减区间为(-∞,0).
答案:(-∞,0)
指数与对数的运算是指数、对数应用的前提,也是研究指数函数与对数函数的基础,不仅是本章考查的重点,也是高考的重要考点之一.
进行指数式的运算时,要注意运算或化简的先后顺序,一般应将负指数转化为正指数、将根式转化为指数式后再计算或化简,同时注意幂的运算性质的应用;对数运算要注意对数运算性质的正用与逆用,注意对底数的转化,对数恒等式以及换底公式的灵活运用,还要注意对数运算与指数运算之间的关系及其合理地转化.专题一专题二专题三专题四专题一专题二专题三专题四?专题一专题二专题三专题四(3)原式=2log32-5log32+2+3log32-5
=2-5=-3.专题一专题二专题三专题四专题一专题二专题三专题四专题二 指数函数、对数函数、幂函数的图象和性质的应用
指数函数、对数函数、幂函数是重要的基本初等函数.它们的图象与性质始终是高考考查的重点.由于指数函数y=ax(a>0,a≠1,x∈R),对数函数y=logax(a>0,a≠1,x>0)的图象与性质都与a的取值有密切的联系,幂函数y=xα的图象与性质与α的取值有关,因此,在a,α的值不确定时,要对它们进行分类讨论,利用图象可以很快捷、直观地解决比较大小、求根等计算问题.专题一专题二专题三专题四应用1函数y=log2(1-x)的图象是( )
解析:由1-x>0得x<1,故函数定义域为(-∞,1),因此排除选项A,B;
又因为t=1-x在(-∞,1)上是单调递减的,
所以y=log2(1-x)在(-∞,1)上是减函数,由此排除D.
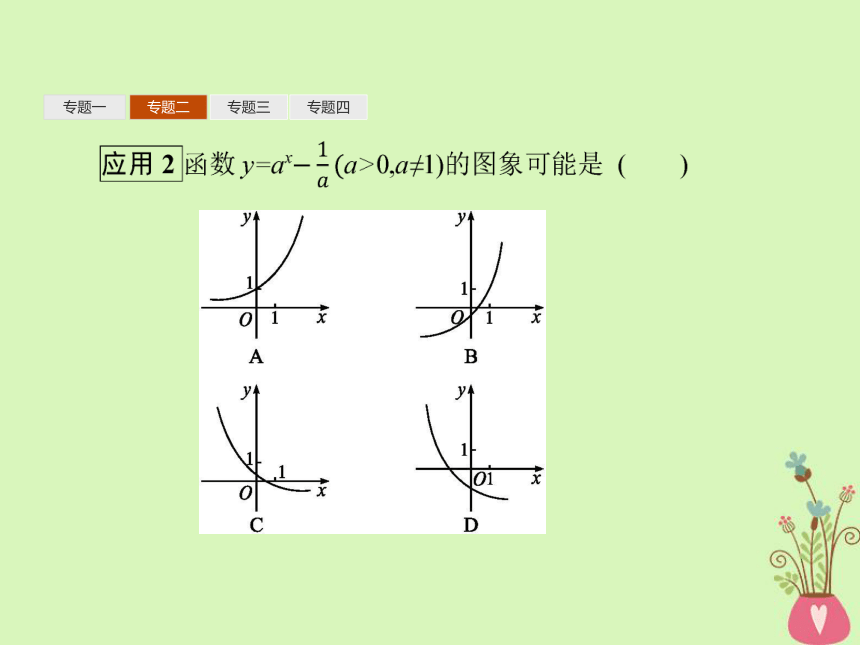
答案:C专题一专题二专题三专题四专题一专题二专题三专题四答案:D 专题一专题二专题三专题四应用3方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
解析:设y1=log3x,y2=-x+3,在同一平面直角坐标系中画出它们的图象如图所示,观察可排除选项A,D.故交点P的横坐标应在区间(1,3)内.
因为当x=2时,y1=log32<1,y2=-2+3=1,且y1是增函数,y2是减函数,
所以交点P的横坐标应在区间(2,3)内.
答案:C专题一专题二专题三专题四应用4若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上单调递减,则a的取值范围为( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)
答案:A专题一专题二专题三专题四专题一专题二专题三专题四专题三 分类讨论思想的应用
分类讨论思想即对问题中的参数不能一概而论,需要按一定的标准进行分别阐述,在分类讨论中要做到“不重复,不遗漏”.专题一专题二专题三专题四提示:将对数不等式统一成同底的形式,再利用分类讨论思想及函数的单调性进行转化求解.专题一专题二专题三专题四提示:按零点分类讨论法即把整个实数集R以±1为分界点分成(-∞,-1],(-1,1),[1,+∞)三段讨论.专题一专题二专题三专题四专题四 函数图象的平移、对称变换
图象变换题因其集数形结合的数学思想、运动变化的观点于一体,又考查了函数图象的画法和相关函数的性质,对于知识的内化、数学能力的提升均起到促进的作用,故在教材乃至高考试题中均占有重要的地位,不容忽视.下面总结一些常见的图象变换规律,供同学们参考.专题一专题二专题三专题四1.图象的平移变换
(1)水平平移:函数y=f(x±a)(a>0)的图象,可由y=f(x)的图象向左(+)或向右(-)平移a个单位长度而得到.
例如,将对数函数y=log2x的图象向左平移2个单位长度,便得到函数y=log2(x+2)的图象.
(2)竖直平移:函数y=f(x)±b(b>0)的图象,可由y=f(x)的图象向上(+)或向下(-)平移b个单位长度而得到.
例如,将指数函数y=x3的图象向下平移1个单位长度,便得到函数y=x3-1的图象.专题一专题二专题三专题四2.图象的对称变换
(1)y=f(-x)与y=f(x)的图象关于y轴对称.
(2)y=-f(x)与y=f(x)的图象关于x轴对称.
(3)y=-f(-x)与y=f(x)的图象关于原点对称.
(4)y=f-1(x)与y=f(x)的图象关于直线y=x对称.
例如,对数函数y=log2x的图象与指数函数y=2x的图象关于直线y=x对称.专题一专题二专题三专题四专题一专题二专题三专题四应用1画出函数y=log4(x2-2x+1)的图象.
提示:先要找出这个函数所对应的基本初等函数,然后利用图象变换向目标靠拢.
解:先对函数解析式进行化简,可得y=log2|x-1|.可直接利用描点法画出y=log2x的图象,而后画出关于y轴的对称变换得到y=log2|x|,再把其向右平移一个单位长度.过程如下:专题一专题二专题三专题四应用2(1)画出函数y=log2(x+2)与y=log2(x-2)的图象,并指出两个图象之间的关系;
(2)画出函数y=f(x)=log2|x|的图象,并根据图象指出它的单调区间.
提示:画函数图象是研究函数变化规律的重要手段,可利用y=log2x的图象进行变换.专题一专题二专题三专题四解:(1)函数y=log2x的图象向右平移2个单位长度就得到y=log2(x-2)的图象;向左平移2个单位长度就得到y=log2(x+2)的图象,
故把y=log2(x+2)的图象向右平移4个单位长度得到y=log2(x-2)的图象(如图所示).专题一专题二专题三专题四(2)当x≠0时,函数y=log2|x|满足f(-x)=log2|-x|=log2|x|=f(x),故y=log2|x|是偶函数,它的图象关于y轴对称.当x>0时,y=log2x.先画出y=log2x(x>0)的图象为C1,再作出C1关于y轴对称的图象C2,C1与C2构成函数y=log2|x|的图象,如图所示.
由图象可知,函数y=log2|x|的单调递减区间是(-∞,0),单调递增区间是(0,+∞).1 2 3 4 5 6 7 8 9 10 11 12
∴x>2,∴f(x)的定义域为(2,+∞).
答案:C1 2 3 4 5 6 7 8 9 10 11 122(北京高考)下列函数中,定义域是R且为增函数的是 ( )
A.y=e-x B.y=x3
C.y=ln x D.y=|x|
解析:A项,函数y=e-x为R上的减函数;
B项,函数y=x3为R上的增函数;
C项,函数y=ln x为(0,+∞)上的增函数;
D项,函数y=|x|在(-∞,0]上为减函数,在(0,+∞)上为增函数.故只有B项符合题意,应选B.
答案:B1 2 3 4 5 6 7 8 9 10 11 12的区间是( )
A.(0,1) B.(1,2)
C.(2,4) D.(4,+∞)答案:C 1 2 3 4 5 6 7 8 9 10 11 124(安徽高考)设a=log37,b=21.1,c=0.83.1,则( )
A.b
∵0<0.83.1<0.80,∴0
A.a>1,c>1
B.a>1,0
D.0
若0
答案:D1 2 3 4 5 6 7 8 9 10 11 127(福建高考)若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )1 2 3 4 5 6 7 8 9 10 11 12?1 2 3 4 5 6 7 8 9 10 11 12答案:D 1 2 3 4 5 6 7 8 9 10 11 121 2 3 4 5 6 7 8 9 10 11 12答案:1 1 2 3 4 5 6 7 8 9 10 11 12答案:(-∞,8]1 2 3 4 5 6 7 8 9 10 11 1212(天津高考)函数f(x)=lg x2的单调递减区间是 .?
解析:函数f(x)=lg x2的定义域为(-∞,0)∪(0,+∞).
∵f(x)=lg x在(0,+∞)上为增函数,y=x2在[0,+∞)上为增函数,在(-∞,0]上为减函数,
∴f(x)=lg x2的单调减区间为(-∞,0).
答案:(-∞,0)
