2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质(第2课时)指数函数性质的应用(19张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质(第2课时)指数函数性质的应用(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 10:55:35 | ||
图片预览





文档简介
课件19张PPT。第2课时 指数函数性质的应用1.能利用指数函数的单调性解不等式、比较大小、求最值.
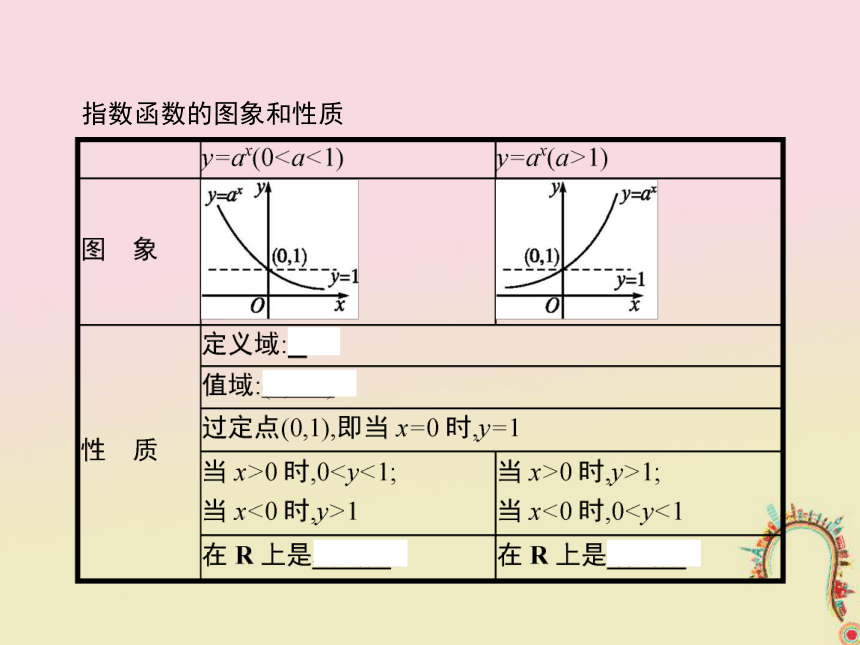
2.掌握指数函数在实际生活中的简单应用,体会指数函数是一类重要的函数模型.指数函数的图象和性质 【做一做1】 已知a=31.03,b=31.04,则( )
A.a>b B.a=b C.a答案:C
【做一做2】 已知指数函数f(x)=ax,且f(3)解析:∵函数f(x)=ax是指数函数,且f(3)∴f(x)在R上是减函数.∴0答案:(0,1)底数对指数函数的影响
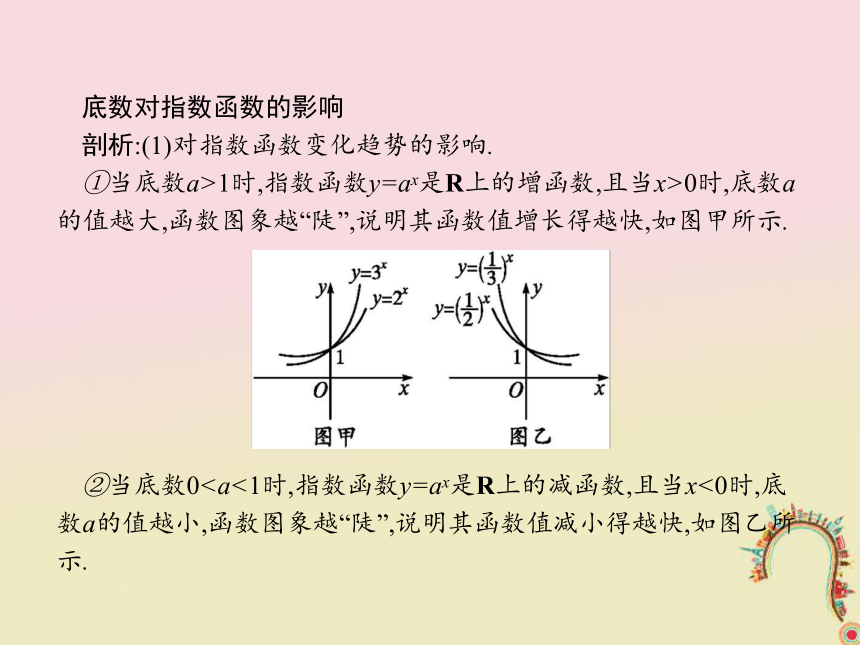
剖析:(1)对指数函数变化趋势的影响.
①当底数a>1时,指数函数y=ax是R上的增函数,且当x>0时,底数a的值越大,函数图象越“陡”,说明其函数值增长得越快,如图甲所示.
②当底数0①若a>b>1,当x<0时,总有00时,总有ax>bx>1.
②若0ax>1;当x=0时,总有ax=bx=1;当x>0时,总有0综上可得,当x>0,a>b>0时,ax>bx;当x<0,a>b>0时,ax【例1】 比较下列各题中两个值的大小:
(1)0.6-1.2,0.6-1.5;
(2)2.3-0.28,0.67-3.1.
分析:(1)构造指数函数,利用其单调性比较大小;(2)利用中间值1比较大小.
解:(1)(单调性法)由于0.6-1.2与0.6-1.5的底数都是0.6,故构造函数y=0.6x,而函数y=0.6x在R上是减函数,又-1.2>-1.5,所以0.6-1.2<0.6-1.5.
(2)(中间量法)由指数函数的性质,知2.3-0.28<2.30=1,0.67-3.1 >0.670=1,所以2.3-0.28<0.67-3.1.题型一题型二题型三题型四反思比较指数值大小的方法:
(1)单调性法:比较同底数幂的大小,可构造指数函数,利用指数函数的单调性比较大小.要注意:明确所给的两个值是哪个指数函数的两个函数值;明确指数函数的底数与1的大小关系.如本例(1).
(2)中间量法:比较不同底数且不同指数幂的大小,常借助中间值1进行比较.如本例(2).题型一题型二题型三题型四【变式训练1】 下列大小关系正确的是( )
A.0.43<30.4<π0
B.0.43<π0<30.4
C.30.4<0.43<π0
D.π0<30.4<0.43
解析:由于30.4>30=1,0.43<0.40=1,π0=1,故0.43<π0<30.4.
答案:B题型一题型二题型三题型四解简单的指数不等式
【例2】 已知a2x+1≤ax-5(a>0,且a≠1),求x的取值范围.
分析:讨论a的取值→得关于x的不等式→解不等式得x的取值范围.
解:当0∴2x+1≥x-5,解得x≥-6;
当a>1时,∵a2x+1≤ax-5,∴2x+1≤x-5,解得x≤-6.
综上所述,当01时,x的取值范围是(-∞,-6].题型一题型二题型三题型四反思解关于x的不等式af(x)>ag(x)(a>0,且a≠1)时,主要依据指数函数的单调性,它的一般步骤为:题型一题型二题型三题型四所以2a+1<22a-3.又y=2x在R上为增函数,
故a+1<2a-3,解得a>4,
故a的取值范围为(4,+∞).
答案:A题型一题型二题型三题型四最值问题
【例3】 已知函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比分析:可结合指数函数f(x)的单调性,对a分类讨论求值.
解:当a>1时,f(x)在区间[1,2]上是增函数,题型一题型二题型三题型四反思指数函数y=ax(a>1)在R上是增函数,则在闭区间[s,t]上,当x=s时,函数取得最小值as;当x=t时,函数取得最大值at.指数函数y=ax(0B.最大值是3,最小值是2解析:设t=x2-2x,x∈[0,3],则t的最大值为3,最小值为-1.又y=2t在R上为增函数,答案:D 题型一题型二题型三题型四应用问题
【例4】 某种储蓄按复利计算利息,若本金为a元,每期利率为r,设存期是x(x∈N*),本利和(本金加上利息)为y元.
(1)写出本利和y随存期x变化的函数解析式;
(2)已知存入本金1 000元,每期利率为2.25%,试计算5期后的本利和.题型一题型二题型三题型四解:(1)已知本金为a元,利率为r,则1期后的本利和为y=a+a×r=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y=a(1+r)3,
……
x期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数解析式为y=a(1+r)x,x∈N*.
(2)将a=1 000,r=2.25%,x=5代入上式,得
y=1 000×(1+2.25%)5
=1 000×1.022 55
≈1 117.68(元),
即5期后的本利和约为1 117.68元.
反思解指数函数的应用问题时,通常利用归纳法得出函数解析式.题型一题型二题型三题型四【变式训练4】 某乡镇现在人均一年占有粮食360 kg,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x(x∈N*)年后人均一年占有y kg粮食,求y关于x的函数解析式.题型一题型二题型三题型四解:设该乡镇现在人口数量为M,则该乡镇现在一年的粮食总产量为360M kg.
1年后,该乡镇粮食总产量为360M(1+4%)kg,人口数量为M(1+1.2%),
2.掌握指数函数在实际生活中的简单应用,体会指数函数是一类重要的函数模型.指数函数的图象和性质 【做一做1】 已知a=31.03,b=31.04,则( )
A.a>b B.a=b C.a答案:C
【做一做2】 已知指数函数f(x)=ax,且f(3)
剖析:(1)对指数函数变化趋势的影响.
①当底数a>1时,指数函数y=ax是R上的增函数,且当x>0时,底数a的值越大,函数图象越“陡”,说明其函数值增长得越快,如图甲所示.
②当底数0
②若0
(1)0.6-1.2,0.6-1.5;
(2)2.3-0.28,0.67-3.1.
分析:(1)构造指数函数,利用其单调性比较大小;(2)利用中间值1比较大小.
解:(1)(单调性法)由于0.6-1.2与0.6-1.5的底数都是0.6,故构造函数y=0.6x,而函数y=0.6x在R上是减函数,又-1.2>-1.5,所以0.6-1.2<0.6-1.5.
(2)(中间量法)由指数函数的性质,知2.3-0.28<2.30=1,0.67-3.1 >0.670=1,所以2.3-0.28<0.67-3.1.题型一题型二题型三题型四反思比较指数值大小的方法:
(1)单调性法:比较同底数幂的大小,可构造指数函数,利用指数函数的单调性比较大小.要注意:明确所给的两个值是哪个指数函数的两个函数值;明确指数函数的底数与1的大小关系.如本例(1).
(2)中间量法:比较不同底数且不同指数幂的大小,常借助中间值1进行比较.如本例(2).题型一题型二题型三题型四【变式训练1】 下列大小关系正确的是( )
A.0.43<30.4<π0
B.0.43<π0<30.4
C.30.4<0.43<π0
D.π0<30.4<0.43
解析:由于30.4>30=1,0.43<0.40=1,π0=1,故0.43<π0<30.4.
答案:B题型一题型二题型三题型四解简单的指数不等式
【例2】 已知a2x+1≤ax-5(a>0,且a≠1),求x的取值范围.
分析:讨论a的取值→得关于x的不等式→解不等式得x的取值范围.
解:当0
当a>1时,∵a2x+1≤ax-5,∴2x+1≤x-5,解得x≤-6.
综上所述,当0
故a+1<2a-3,解得a>4,
故a的取值范围为(4,+∞).
答案:A题型一题型二题型三题型四最值问题
【例3】 已知函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比分析:可结合指数函数f(x)的单调性,对a分类讨论求值.
解:当a>1时,f(x)在区间[1,2]上是增函数,题型一题型二题型三题型四反思指数函数y=ax(a>1)在R上是增函数,则在闭区间[s,t]上,当x=s时,函数取得最小值as;当x=t时,函数取得最大值at.指数函数y=ax(0
【例4】 某种储蓄按复利计算利息,若本金为a元,每期利率为r,设存期是x(x∈N*),本利和(本金加上利息)为y元.
(1)写出本利和y随存期x变化的函数解析式;
(2)已知存入本金1 000元,每期利率为2.25%,试计算5期后的本利和.题型一题型二题型三题型四解:(1)已知本金为a元,利率为r,则1期后的本利和为y=a+a×r=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y=a(1+r)3,
……
x期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数解析式为y=a(1+r)x,x∈N*.
(2)将a=1 000,r=2.25%,x=5代入上式,得
y=1 000×(1+2.25%)5
=1 000×1.022 55
≈1 117.68(元),
即5期后的本利和约为1 117.68元.
反思解指数函数的应用问题时,通常利用归纳法得出函数解析式.题型一题型二题型三题型四【变式训练4】 某乡镇现在人均一年占有粮食360 kg,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x(x∈N*)年后人均一年占有y kg粮食,求y关于x的函数解析式.题型一题型二题型三题型四解:设该乡镇现在人口数量为M,则该乡镇现在一年的粮食总产量为360M kg.
1年后,该乡镇粮食总产量为360M(1+4%)kg,人口数量为M(1+1.2%),
