2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质(第1课时)对数函数的图象和性质(23张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质(第1课时)对数函数的图象和性质(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 702.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 10:57:30 | ||
图片预览







文档简介
课件23张PPT。2.2.2 对数函数及其性质第1课时 对数函数的图象和性质1.掌握对数函数的概念,会判断对数函数.
2.初步掌握对数函数的图象和性质.
3.能利用对数函数的性质解决与对数函数有关的定义域、定点问题.1.对数函数的定义
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).
归纳总结1.由于指数函数y=ax中的底数a满足a>0,且a≠1,则对数函数y=logax中的底数a也必须满足a>0,且a≠1.
2.对数函数的解析式同时满足:(1)对数符号前面的系数是1;(2)对数的底数是不等于1的正实数(常数);(3)对数的真数仅有自变量x.
【做一做1】 下列函数是对数函数的是( )
A.y=ln x B.y=ln(x+1)
C.y=logxe D.y=logxx
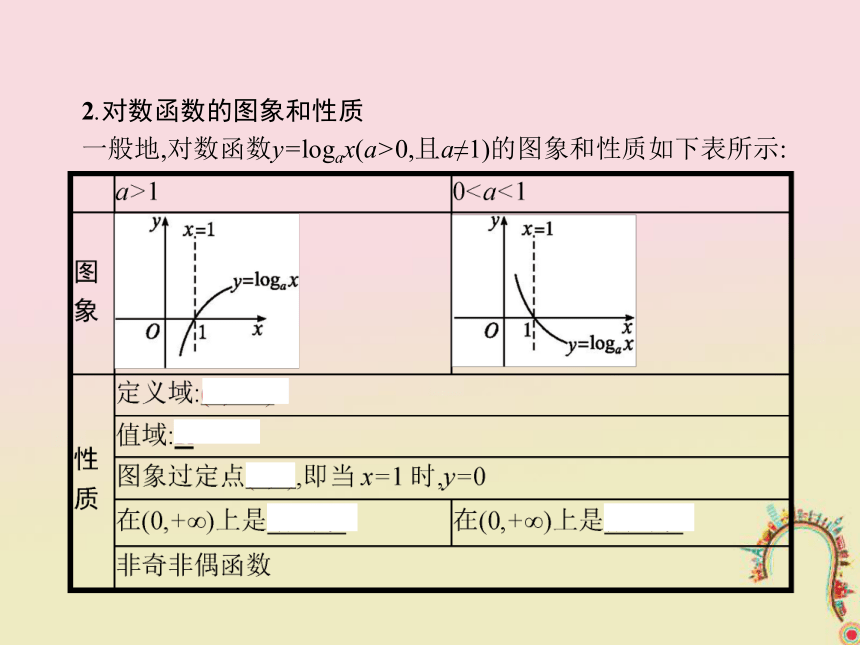
答案:A2.对数函数的图象和性质
一般地,对数函数y=logax(a>0,且a≠1)的图象和性质如下表所示:归纳总结对数函数的知识总结:
对数增减有思路,函数图象看底数;
底数只能大于0,等于1来可不行;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
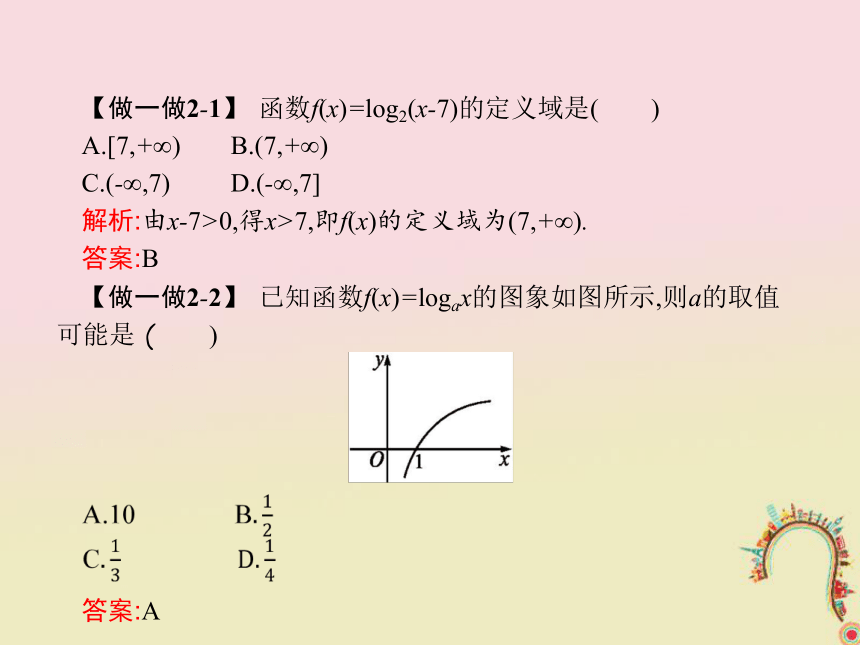
无论函数增和减,图象都过(1,0)点.【做一做2-1】 函数f(x)=log2(x-7)的定义域是( )
A.[7,+∞) B.(7,+∞)
C.(-∞,7) D.(-∞,7]
解析:由x-7>0,得x>7,即f(x)的定义域为(7,+∞).
答案:B
【做一做2-2】 已知函数f(x)=logax的图象如图所示,则a的取值可能是 ( )答案:A 3.反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为反函数.它们的图象关于直线y=x对称.
【做一做3】 函数y=ln x的反函数是 .?
答案:y=ex对数函数和指数函数的区别与联系
剖析:将对数函数和指数函数的性质对比列表如下:题型一题型二题型三题型四对数函数的概念
【例1】 下列函数中,哪些是对数函数?
(1)y=logax2(a>0,且a≠1);
(2)y=log2x-1;
(3)y=2log8x;
(4)y=logxa(x>0,且x≠1);
(5)y=log5x.
分析:根据对数函数的定义进行判断.题型一题型二题型三题型四解:只有(5)为对数函数.
(1)中真数不是自变量x,故不是对数函数;
(2)中是对数式减1,故不是对数函数;
(3)中log8x前的系数是2,而不是1,
故不是对数函数;
(4)中底数是自变量x,而非常数a,故不是对数函数.题型一题型二题型三题型四【变式训练1】 若函数f(x)=(a2-a+1)log(a+1)x是对数函数,则实数a= .?
解得a=1.
答案:1题型一题型二题型三题型四求定义域解得x<4,且x≠3,
故函数的定义域为(-∞,3)∪(3,4).
反思求与对数函数有关的函数的定义域时,除了已学习过的求函数定义域的方法外,还要注意对数的真数大于零.特别地,函数y=logaf(x)的定义域是使f(x)>0的x的取值范围.题型一题型二题型三题型四A.[4,+∞) B.(10,+∞)
C.(4,10)∪(10,+∞) D.[4,10)∪(10,+∞)答案:D 题型一题型二题型三题型四对数函数的图象问题
【例3】 (1)已知函数f(x)=loga(x+1)+1(a>0,且a≠1)的图象恒过定点P,则点P的坐标是 .?
(2)对数函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a,b,c,d,1,0的大小关系为 .?题型一题型二题型三题型四解析:(1)令x+1=1,得x=0,
则f(0)=loga1+1=1,即定点P的坐标为(0,1).
(2)由题图可知函数y=logax,y=logbx的底数a>1,b>1,函数y=logcx,y=logdx的底数0过点(0,1)作平行于x轴的直线l(图略),则直线l与四条曲线交点的横坐标从左向右依次为c,d,a,b,显然b>a>1>d>c>0.
答案:(1)(0,1) (2)b>a>1>d>c>0题型一题型二题型三题型四反思1.对数函数的图象过定点问题
求函数y=m+logaf(x)(a>0,且a≠1)的图象过定点时,只需令f(x)=1求出x,即得定点为(x,m).
2.根据对数函数图象判断底数大小的方法
作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.题型一题型二题型三题型四【变式训练3】 (1)已知函数f(x)=loga(x-m)+n的图象恒过点(3,5),则lg m+lg n等于( )(2)已知ab=1,函数f(x)=ax(a>0,且a≠1)与函数g(x)=-logbx(b>0,且b≠1)的图象可能是( )题型一题型二题型三题型四若0若a>1,则函数f(x)=ax的图象上升且过点(0,1),函数g(x)=logax的图象上升且过点(1,0),只有选项B中图象符合.
答案:(1)C (2)B题型一题型二题型三题型四易混易错题
易错点 忽略对数函数的定义域致错
【例4】 已知函数y=f(x),x,y满足关系式lg(lg y)=lg(3-x),求函数y=f(x)的解析式及定义域、值域.
错解∵lg(lg y)=lg(3-x),∴lg y=3-x,
∴y=103-x,定义域为R,值域为(0,+∞).
错因分析:错解没有注意到对数函数的定义域,即已知关系式成题型一题型二题型三题型四正解:∵lg(lg y)=lg(3-x), ∴y>103-3=1,
∴y=f(x)的定义域为(-∞,3),值域是(1,+∞).
反思解决含有对数的问题时,一定要使对数式有意义,即要使对数的真数大于0,底数大于0且不等于1.题型一题型二题型三题型四当x=2时,f(2)=0.故定点P的坐标为(2,0).
答案:(2,0)
2.初步掌握对数函数的图象和性质.
3.能利用对数函数的性质解决与对数函数有关的定义域、定点问题.1.对数函数的定义
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).
归纳总结1.由于指数函数y=ax中的底数a满足a>0,且a≠1,则对数函数y=logax中的底数a也必须满足a>0,且a≠1.
2.对数函数的解析式同时满足:(1)对数符号前面的系数是1;(2)对数的底数是不等于1的正实数(常数);(3)对数的真数仅有自变量x.
【做一做1】 下列函数是对数函数的是( )
A.y=ln x B.y=ln(x+1)
C.y=logxe D.y=logxx
答案:A2.对数函数的图象和性质
一般地,对数函数y=logax(a>0,且a≠1)的图象和性质如下表所示:归纳总结对数函数的知识总结:
对数增减有思路,函数图象看底数;
底数只能大于0,等于1来可不行;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(1,0)点.【做一做2-1】 函数f(x)=log2(x-7)的定义域是( )
A.[7,+∞) B.(7,+∞)
C.(-∞,7) D.(-∞,7]
解析:由x-7>0,得x>7,即f(x)的定义域为(7,+∞).
答案:B
【做一做2-2】 已知函数f(x)=logax的图象如图所示,则a的取值可能是 ( )答案:A 3.反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为反函数.它们的图象关于直线y=x对称.
【做一做3】 函数y=ln x的反函数是 .?
答案:y=ex对数函数和指数函数的区别与联系
剖析:将对数函数和指数函数的性质对比列表如下:题型一题型二题型三题型四对数函数的概念
【例1】 下列函数中,哪些是对数函数?
(1)y=logax2(a>0,且a≠1);
(2)y=log2x-1;
(3)y=2log8x;
(4)y=logxa(x>0,且x≠1);
(5)y=log5x.
分析:根据对数函数的定义进行判断.题型一题型二题型三题型四解:只有(5)为对数函数.
(1)中真数不是自变量x,故不是对数函数;
(2)中是对数式减1,故不是对数函数;
(3)中log8x前的系数是2,而不是1,
故不是对数函数;
(4)中底数是自变量x,而非常数a,故不是对数函数.题型一题型二题型三题型四【变式训练1】 若函数f(x)=(a2-a+1)log(a+1)x是对数函数,则实数a= .?
解得a=1.
答案:1题型一题型二题型三题型四求定义域解得x<4,且x≠3,
故函数的定义域为(-∞,3)∪(3,4).
反思求与对数函数有关的函数的定义域时,除了已学习过的求函数定义域的方法外,还要注意对数的真数大于零.特别地,函数y=logaf(x)的定义域是使f(x)>0的x的取值范围.题型一题型二题型三题型四A.[4,+∞) B.(10,+∞)
C.(4,10)∪(10,+∞) D.[4,10)∪(10,+∞)答案:D 题型一题型二题型三题型四对数函数的图象问题
【例3】 (1)已知函数f(x)=loga(x+1)+1(a>0,且a≠1)的图象恒过定点P,则点P的坐标是 .?
(2)对数函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a,b,c,d,1,0的大小关系为 .?题型一题型二题型三题型四解析:(1)令x+1=1,得x=0,
则f(0)=loga1+1=1,即定点P的坐标为(0,1).
(2)由题图可知函数y=logax,y=logbx的底数a>1,b>1,函数y=logcx,y=logdx的底数0
答案:(1)(0,1) (2)b>a>1>d>c>0题型一题型二题型三题型四反思1.对数函数的图象过定点问题
求函数y=m+logaf(x)(a>0,且a≠1)的图象过定点时,只需令f(x)=1求出x,即得定点为(x,m).
2.根据对数函数图象判断底数大小的方法
作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.题型一题型二题型三题型四【变式训练3】 (1)已知函数f(x)=loga(x-m)+n的图象恒过点(3,5),则lg m+lg n等于( )(2)已知ab=1,函数f(x)=ax(a>0,且a≠1)与函数g(x)=-logbx(b>0,且b≠1)的图象可能是( )题型一题型二题型三题型四若0
答案:(1)C (2)B题型一题型二题型三题型四易混易错题
易错点 忽略对数函数的定义域致错
【例4】 已知函数y=f(x),x,y满足关系式lg(lg y)=lg(3-x),求函数y=f(x)的解析式及定义域、值域.
错解∵lg(lg y)=lg(3-x),∴lg y=3-x,
∴y=103-x,定义域为R,值域为(0,+∞).
错因分析:错解没有注意到对数函数的定义域,即已知关系式成题型一题型二题型三题型四正解:∵lg(lg y)=lg(3-x), ∴y>103-3=1,
∴y=f(x)的定义域为(-∞,3),值域是(1,+∞).
反思解决含有对数的问题时,一定要使对数式有意义,即要使对数的真数大于0,底数大于0且不等于1.题型一题型二题型三题型四当x=2时,f(2)=0.故定点P的坐标为(2,0).
答案:(2,0)
