2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)本章整合(34张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第二章基本初等函数(Ⅰ)本章整合(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 11:00:27 | ||
图片预览










文档简介
课件34张PPT。本章整合基本初等函数(Ⅰ) 基本初等函数(Ⅰ) 基本初等函数(Ⅰ) 专题一专题二专题三专题四专题一 指数、对数的有关运算问题
指数与指数运算、对数与对数运算是两个重要的知识点,它们既是学习和研究指数函数、对数函数的基础,也是高考必考内容之一,学习时应引起足够的重视.提示:利用对数的运算性质把前三项合起来, 专题一专题二专题三专题四提示:转化为求logaA,用logax和logay表示logaA后,再将logax=4和logay=5代入.专题一专题二专题三专题四专题二 指数函数、对数函数、幂函数的定义域和值域的应用
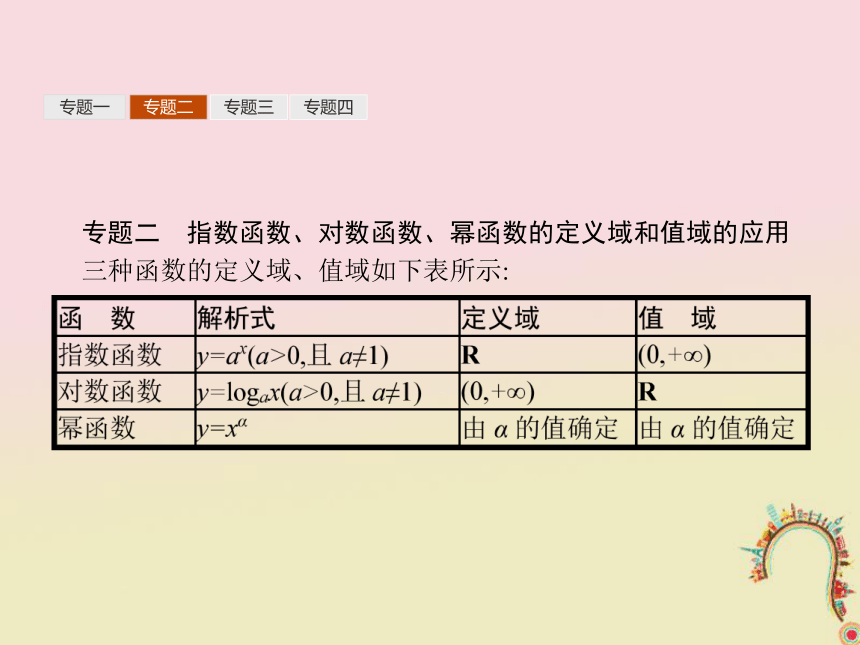
三种函数的定义域、值域如下表所示:专题一专题二专题三专题四提示:要保证分母不等于0、被开方数为非负数、对数的真数为正数,由此列出不等式组求解.专题一专题二专题三专题四提示:令t=x2-2x+2,先求出t的值域, 又t=x2-2x+2=(x-1)2+1,0≤x≤3,
∴当x=1时,tmin=1;当x=3时,tmax=5.故1≤t≤5,专题一专题二专题三专题四应用3已知不等式2x+3-2m>0在区间[0,+∞)内恒成立,求实数m的取值范围.
提示:g(m)f(x)恒成立,只需g(m)大于f(x)的最大值.
解:原不等式可变形为2m-3<2x,要使此不等式在区间[0,+∞)内恒成立,只需2m-3小于y=2x在区间[0,+∞)内的最小值.当x∈[0,+∞)时,由y=2x的单调性可知y=2x在区间[0,+∞)内的最小值是20=1,所以有2m-3<1,解得m<2.故实数m的取值范围为(-∞,2).专题一专题二专题三专题四专题三 指数函数、对数函数图象的应用
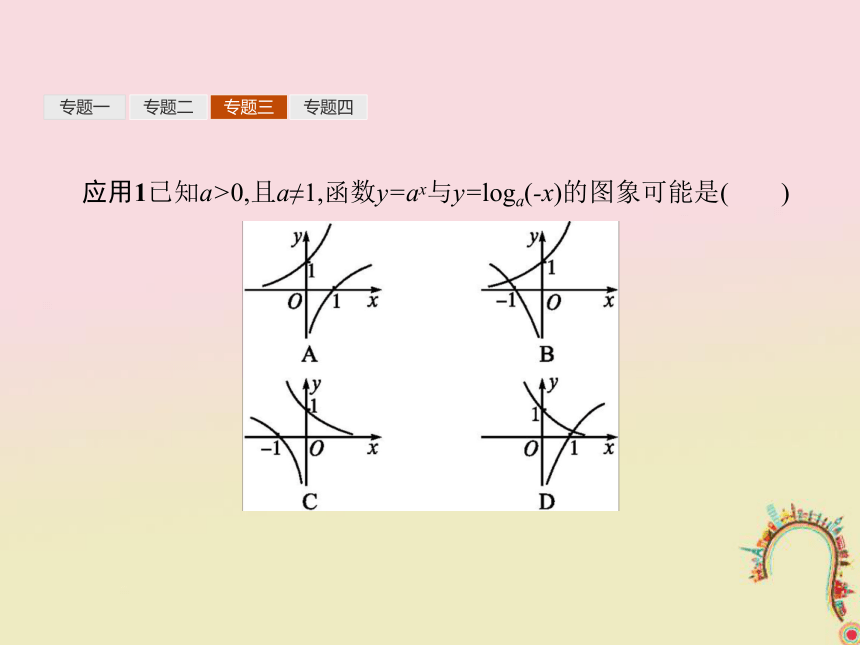
指数函数、对数函数图象的应用有两个方面:一是已知函数解析式求作函数图象,即“知式求图”,此类题目往往是选择题,常借助于指数函数、对数函数的图象特征来解决;二是判断方程的根的个数时,通常不具体解方程,而是转化为判断指数函数、对数函数等图象的交点个数问题.这就要求画指数函数、对数函数的图象时尽量准确,特别是一些关键点要正确,比如,指数函数的图象必过点(0,1),对数函数的图象必过点(1,0).专题一专题二专题三专题四应用1已知a>0,且a≠1,函数y=ax与y=loga(-x)的图象可能是( )专题一专题二专题三专题四提示:先由函数的定义域判断函数图象的位置,再对底数a进行讨论,最后确定选项.
解析:由y=loga(-x)的定义域为(-∞,0)知,图象应在y轴左侧,可排除A,D选项.当a>1时,y=ax应为增函数,y=loga(-x)应为减函数,可知B项正确;而对C项,由y=ax的图象知y=ax为减函数,则0答案:B专题一专题二专题三专题四应用2若直线y=2a与函数y=|ax-1|+1(a>0,且a≠1)的图象有两个公共点,则a的取值范围是 .?
提示:画出y=|ax-1|+1的图象,转化为此图象与直线y=2a有两个交点,观察图象即得所求结果,注意分01两种情况的图象处理.专题一专题二专题三专题四解析:当a>1时,通过平移变换和翻折变换可得如图(1)所示的图象,专题一专题二专题三专题四专题四 指数函数、对数函数、幂函数的单调性的应用
1.解指数不等式、对数不等式
求解指数不等式、对数不等式时,一般是利用指数函数、对数函数的单调性去掉底数,转化为关于指数或真数的不等式,再求解.特别地,解对数不等式时,要防止定义域扩大,应在解的过程中加上限制条件,使定义域保持不变,即进行同解变形.若非同解变形,最后一定要检验.专题一专题二专题三专题四应用1(1)已知3x≥30.5,求实数x的取值范围;
(2)已知0.2x<25,求实数x的取值范围.
提示:(1)构造指数函数,利用指数函数的单调性求解;(2)将式子转化为同底的指数式,然后利用指数函数的单调性求解.
解:(1)因为3>1,所以指数函数f(x)=3x在R上是增函数.由3x≥30.5,可得x≥0.5,即x的取值范围为[0.5,+∞).
(2)因为0<0.2<1,所以指数函数f(x)=0.2x在R上是减函数.由此可得x>-2,即x的取值范围为(-2,+∞). 专题一专题二专题三专题四(2)求满足不等式log3x<1的x的取值范围;
提示:将常数1转化为对数式的形式,构造对数函数,利用对数函数的单调性求解.所以x的取值范围为0求形如函数y=f(ax)和y=f(logax)的定义域时,往往把ax和logax看成一个整体,列出关于ax和logax的不等式(组),解得定义域.解析:要使函数有意义,则需6x-36≥0,
即6x≥62.又函数y=6x在R上是增函数,则x≥2.
答案:[2,+∞)解析:要使函数有意义,则需1-log3x≥0,即log3x≤1=log33.又函数y=log3x在区间(0,+∞)内是增函数,则x≤3.又x>0,则0答案:(0,3]专题一专题二专题三专题四3.比较大小
比较几个数的大小是指数函数、对数函数、幂函数的单调性的又一重要应用,其基本方法是,将需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较,有时也采用中间量法、图象法、特殊值法等方法.专题一专题二专题三专题四A.a提示:分别判断a,b,c与0和1的大小,利用中间量法比较大小.答案:A 专题一专题二专题三专题四应用2已知c<0,则下列不等式成立的是( ) 提示:思路一(图象法):在同一坐标系中画出函数y=x, 思路二(特殊值法):c取特殊值,排除错误选项. 专题一专题二专题三专题四答案:C 1 2 3 4 5 6 7 8 9 101(2018·全国Ⅲ高考)下列函数中,其图象与函数y=ln x的图象关于直线x=1对称的是( )
A.y=ln(1-x) B.y=ln(2-x)
C.y=ln(1+x) D.y=ln(2+x)
解析:设所求函数的图象上点P(x,y)关于x=1对称的点为Q(2-x,y),由题意知Q在y=ln x上,
∴y=ln(2-x),故选B.
答案:B1 2 3 4 5 6 7 8 9 10A.(-∞,-1] B.(0,+∞)
C.(-1,0) D.(-∞,0)
解析:画出函数f(x)的图象如图所示,由图可知:
①当x+1≥0且2x≥0,即x≥0时,f(2x)=f(x+1),不满足题意;
②当x+1>0且2x<0,即-1③当x+1≤0时,x≤-1,此时2x<0,若f(x+1)2x,解得x<1.故x≤-1.
综上所述,x的取值范围为(-∞,0).
答案:D1 2 3 4 5 6 7 8 9 103(2017·全国Ⅰ高考)已知函数f(x)=ln x+ln(2-x),则( )
A.f(x)在区间(0,2)内单调递增
B.f(x)在区间(0,2)内单调递减
C.y=f(x)的图象关于直线x=1对称
D.y=f(x)的图象关于点(1,0)对称
解析:f(x)=ln x+ln(2-x)=ln(-x2+2x),x∈(0,2).当x∈(0,1)时,x增大, -x2+2x增大,ln(-x2+2x)增大,当x∈(1,2)时,x增大,-x2+2x减小, ln(-x2+2x)减小,即f(x)在区间(0,1)单调递增,在区间(1,2)单调递减,故排除选项A,B;因为f(2-x)=ln(2-x)+ln[2-(2-x)]=ln(2-x)+ln x=f(x),所以y=f(x)的图象关于直线x=1对称,故排除选项D.故选C.
答案:C1 2 3 4 5 6 7 8 9 104(2018·全国Ⅲ高考)设a=log0.20.3,b=log20.3,则( )
A.a+bC.a+b<0解析:∵a=log0.20.3>0,b=log20.3<0,∴ab<0.而lg 2-1<0,2lg 2-1<0,lg 3-1<0,lg 2>0,
∴a+b<0.答案:B 1 2 3 4 5 6 7 8 9 101 2 3 4 5 6 7 8 9 10答案:B 1 2 3 4 5 6 7 8 9 106(2017·全国Ⅰ高考)已知集合A={x|x<1},B={x|3x<1},则( )
A.A∩B={x|x<0} B.A∪B=R
C.A∪B={x|x>1} D.A∩B=?
解析:∵3x<1=30,∴x<0,∴B={x|x<0},
∴A∩B={x|x<0},A∪B={x|x<1}.故选A.
答案:A1 2 3 4 5 6 7 8 9 10A.是偶函数,且在R上是增函数
B.是奇函数,且在R上是增函数
C.是偶函数,且在R上是减函数
D.是奇函数,且在R上是减函数数.故选B.
答案:B1 2 3 4 5 6 7 8 9 108(2017·全国Ⅱ高考)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1) C.(1,+∞) D.(4,+∞)
解析:由题意可知x2-2x-8>0,解得x<-2或x>4.故定义域为(-∞,-2) ∪(4,+∞),易知t=x2-2x-8在(-∞,-2)内单调递减,在(4,+∞)内单调递增.因为y=ln t在t∈(0,+∞)内单调递增,依据复合函数单调性的同增异减原则,可得函数f(x)的单调递增区间为(4,+∞).故选D.
答案:D1 2 3 4 5 6 7 8 9 109(2018·全国Ⅰ高考)已知函数f(x)=log2(x2+a),若f(3)=1,则a= .?
解析:因为f(3)=log2(9+a)=1,所以9+a=2,即a=-7.
答案:-71 2 3 4 5 6 7 8 9 10∴g(x)+g(-x)=ln(1+x2-x2)=0,
∴g(x)为奇函数.∴f(x)=g(x)+1.
∴f(a)+f(-a)=g(a)+1+g(-a)+1=2.
∴f(-a)=-2.
答案:-2
指数与指数运算、对数与对数运算是两个重要的知识点,它们既是学习和研究指数函数、对数函数的基础,也是高考必考内容之一,学习时应引起足够的重视.提示:利用对数的运算性质把前三项合起来, 专题一专题二专题三专题四提示:转化为求logaA,用logax和logay表示logaA后,再将logax=4和logay=5代入.专题一专题二专题三专题四专题二 指数函数、对数函数、幂函数的定义域和值域的应用
三种函数的定义域、值域如下表所示:专题一专题二专题三专题四提示:要保证分母不等于0、被开方数为非负数、对数的真数为正数,由此列出不等式组求解.专题一专题二专题三专题四提示:令t=x2-2x+2,先求出t的值域, 又t=x2-2x+2=(x-1)2+1,0≤x≤3,
∴当x=1时,tmin=1;当x=3时,tmax=5.故1≤t≤5,专题一专题二专题三专题四应用3已知不等式2x+3-2m>0在区间[0,+∞)内恒成立,求实数m的取值范围.
提示:g(m)
解:原不等式可变形为2m-3<2x,要使此不等式在区间[0,+∞)内恒成立,只需2m-3小于y=2x在区间[0,+∞)内的最小值.当x∈[0,+∞)时,由y=2x的单调性可知y=2x在区间[0,+∞)内的最小值是20=1,所以有2m-3<1,解得m<2.故实数m的取值范围为(-∞,2).专题一专题二专题三专题四专题三 指数函数、对数函数图象的应用
指数函数、对数函数图象的应用有两个方面:一是已知函数解析式求作函数图象,即“知式求图”,此类题目往往是选择题,常借助于指数函数、对数函数的图象特征来解决;二是判断方程的根的个数时,通常不具体解方程,而是转化为判断指数函数、对数函数等图象的交点个数问题.这就要求画指数函数、对数函数的图象时尽量准确,特别是一些关键点要正确,比如,指数函数的图象必过点(0,1),对数函数的图象必过点(1,0).专题一专题二专题三专题四应用1已知a>0,且a≠1,函数y=ax与y=loga(-x)的图象可能是( )专题一专题二专题三专题四提示:先由函数的定义域判断函数图象的位置,再对底数a进行讨论,最后确定选项.
解析:由y=loga(-x)的定义域为(-∞,0)知,图象应在y轴左侧,可排除A,D选项.当a>1时,y=ax应为增函数,y=loga(-x)应为减函数,可知B项正确;而对C项,由y=ax的图象知y=ax为减函数,则0
提示:画出y=|ax-1|+1的图象,转化为此图象与直线y=2a有两个交点,观察图象即得所求结果,注意分0
1.解指数不等式、对数不等式
求解指数不等式、对数不等式时,一般是利用指数函数、对数函数的单调性去掉底数,转化为关于指数或真数的不等式,再求解.特别地,解对数不等式时,要防止定义域扩大,应在解的过程中加上限制条件,使定义域保持不变,即进行同解变形.若非同解变形,最后一定要检验.专题一专题二专题三专题四应用1(1)已知3x≥30.5,求实数x的取值范围;
(2)已知0.2x<25,求实数x的取值范围.
提示:(1)构造指数函数,利用指数函数的单调性求解;(2)将式子转化为同底的指数式,然后利用指数函数的单调性求解.
解:(1)因为3>1,所以指数函数f(x)=3x在R上是增函数.由3x≥30.5,可得x≥0.5,即x的取值范围为[0.5,+∞).
(2)因为0<0.2<1,所以指数函数f(x)=0.2x在R上是减函数.由此可得x>-2,即x的取值范围为(-2,+∞). 专题一专题二专题三专题四(2)求满足不等式log3x<1的x的取值范围;
提示:将常数1转化为对数式的形式,构造对数函数,利用对数函数的单调性求解.所以x的取值范围为0
即6x≥62.又函数y=6x在R上是增函数,则x≥2.
答案:[2,+∞)解析:要使函数有意义,则需1-log3x≥0,即log3x≤1=log33.又函数y=log3x在区间(0,+∞)内是增函数,则x≤3.又x>0,则0
比较几个数的大小是指数函数、对数函数、幂函数的单调性的又一重要应用,其基本方法是,将需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较,有时也采用中间量法、图象法、特殊值法等方法.专题一专题二专题三专题四A.a
A.y=ln(1-x) B.y=ln(2-x)
C.y=ln(1+x) D.y=ln(2+x)
解析:设所求函数的图象上点P(x,y)关于x=1对称的点为Q(2-x,y),由题意知Q在y=ln x上,
∴y=ln(2-x),故选B.
答案:B1 2 3 4 5 6 7 8 9 10A.(-∞,-1] B.(0,+∞)
C.(-1,0) D.(-∞,0)
解析:画出函数f(x)的图象如图所示,由图可知:
①当x+1≥0且2x≥0,即x≥0时,f(2x)=f(x+1),不满足题意;
②当x+1>0且2x<0,即-1
综上所述,x的取值范围为(-∞,0).
答案:D1 2 3 4 5 6 7 8 9 103(2017·全国Ⅰ高考)已知函数f(x)=ln x+ln(2-x),则( )
A.f(x)在区间(0,2)内单调递增
B.f(x)在区间(0,2)内单调递减
C.y=f(x)的图象关于直线x=1对称
D.y=f(x)的图象关于点(1,0)对称
解析:f(x)=ln x+ln(2-x)=ln(-x2+2x),x∈(0,2).当x∈(0,1)时,x增大, -x2+2x增大,ln(-x2+2x)增大,当x∈(1,2)时,x增大,-x2+2x减小, ln(-x2+2x)减小,即f(x)在区间(0,1)单调递增,在区间(1,2)单调递减,故排除选项A,B;因为f(2-x)=ln(2-x)+ln[2-(2-x)]=ln(2-x)+ln x=f(x),所以y=f(x)的图象关于直线x=1对称,故排除选项D.故选C.
答案:C1 2 3 4 5 6 7 8 9 104(2018·全国Ⅲ高考)设a=log0.20.3,b=log20.3,则( )
A.a+b
∴a+b<0.答案:B 1 2 3 4 5 6 7 8 9 101 2 3 4 5 6 7 8 9 10答案:B 1 2 3 4 5 6 7 8 9 106(2017·全国Ⅰ高考)已知集合A={x|x<1},B={x|3x<1},则( )
A.A∩B={x|x<0} B.A∪B=R
C.A∪B={x|x>1} D.A∩B=?
解析:∵3x<1=30,∴x<0,∴B={x|x<0},
∴A∩B={x|x<0},A∪B={x|x<1}.故选A.
答案:A1 2 3 4 5 6 7 8 9 10A.是偶函数,且在R上是增函数
B.是奇函数,且在R上是增函数
C.是偶函数,且在R上是减函数
D.是奇函数,且在R上是减函数数.故选B.
答案:B1 2 3 4 5 6 7 8 9 108(2017·全国Ⅱ高考)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1) C.(1,+∞) D.(4,+∞)
解析:由题意可知x2-2x-8>0,解得x<-2或x>4.故定义域为(-∞,-2) ∪(4,+∞),易知t=x2-2x-8在(-∞,-2)内单调递减,在(4,+∞)内单调递增.因为y=ln t在t∈(0,+∞)内单调递增,依据复合函数单调性的同增异减原则,可得函数f(x)的单调递增区间为(4,+∞).故选D.
答案:D1 2 3 4 5 6 7 8 9 109(2018·全国Ⅰ高考)已知函数f(x)=log2(x2+a),若f(3)=1,则a= .?
解析:因为f(3)=log2(9+a)=1,所以9+a=2,即a=-7.
答案:-71 2 3 4 5 6 7 8 9 10∴g(x)+g(-x)=ln(1+x2-x2)=0,
∴g(x)为奇函数.∴f(x)=g(x)+1.
∴f(a)+f(-a)=g(a)+1+g(-a)+1=2.
∴f(-a)=-2.
答案:-2
