2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.1.3集合与函数概念(第2课时)补集(22张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.1.3集合与函数概念(第2课时)补集(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 627.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览






文档简介
课件22张PPT。第2课时 补集1.理解全集、补集的含义,会求给定集合的补集.
2.能够解决交集、并集、补集的综合运算问题.
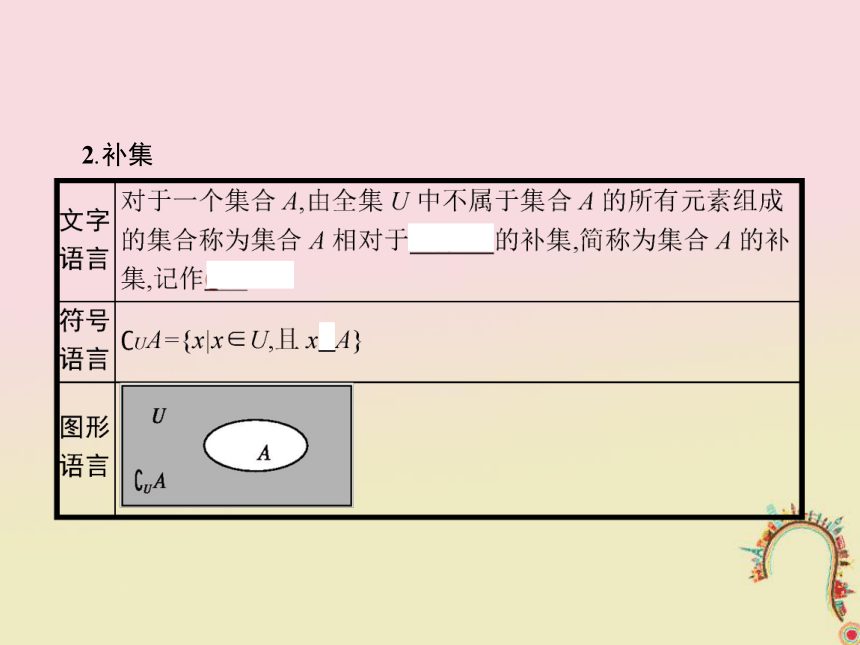
3.能借助Venn图,利用集合运算解决有关的实际应用问题.1.全集 2.补集 归纳总结1.简单地说,?UA是从全集U中取出集合A的全部元素之后,所有剩余的元素组成的集合.
2.性质:A∪(?UA)=U,A∩(?UA)=?,?U(?UA)=A,?UU=?,?U?=U,?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
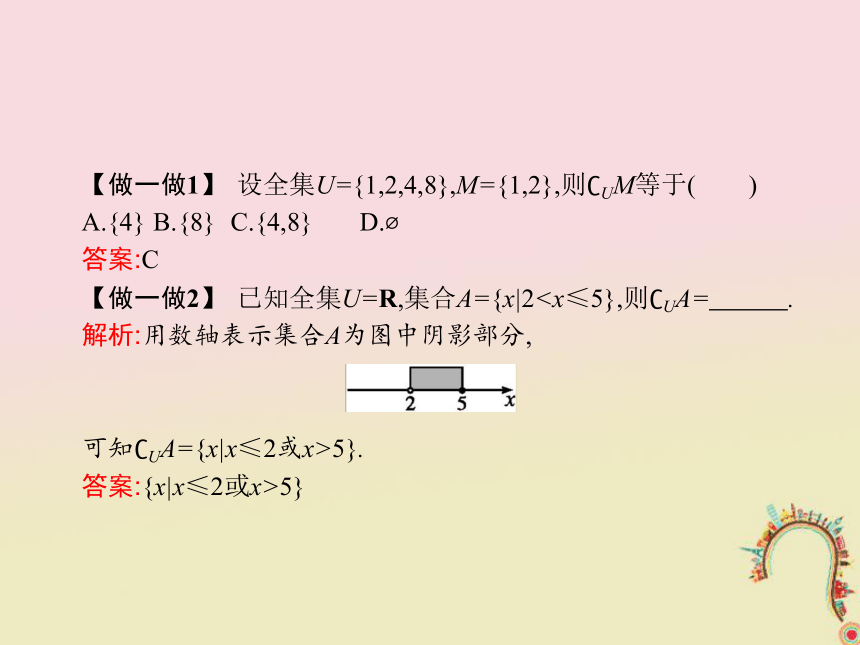
3.如图,阴影部分是常用到的含有两个集合运算结果的Venn图表示.【做一做1】 设全集U={1,2,4,8},M={1,2},则?UM等于( )
A.{4} B.{8} C.{4,8} D.?
答案:C
【做一做2】 已知全集U=R,集合A={x|2解析:用数轴表示集合A为图中阴影部分,
可知?UA={x|x≤2或x>5}.
答案:{x|x≤2或x>5}?AC与?BC不一定相等
剖析依据补集的含义,符号?AC和?BC都表示集合C的补集,但是?AC表示集合C在全集A中的补集,而?BC表示集合C在全集B中的补集;因为集合A和B不一定相等,所以?AC与?BC不一定相等.因此,求集合的补集时,首先要明确全集,否则容易出错.如若集合A={1,2,3,4,5,6,7,8,9},B={0,1,2,3,4},C={1,3,4},则?AC={2,5,6,7,8,9},?BC={0,2},很明显?AC≠?BC.题型一题型二题型三题型四题型五补集运算问题
【例1】 (1)已知全集U,集合A={1,3,5,7},?UA={2,4,6},?UB={1,4,6},则集合B= .?
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则?UA= .?
分析:(1)由A及?UA求出全集U,再由补集定义求出集合B,或利用Venn图求出集合B.
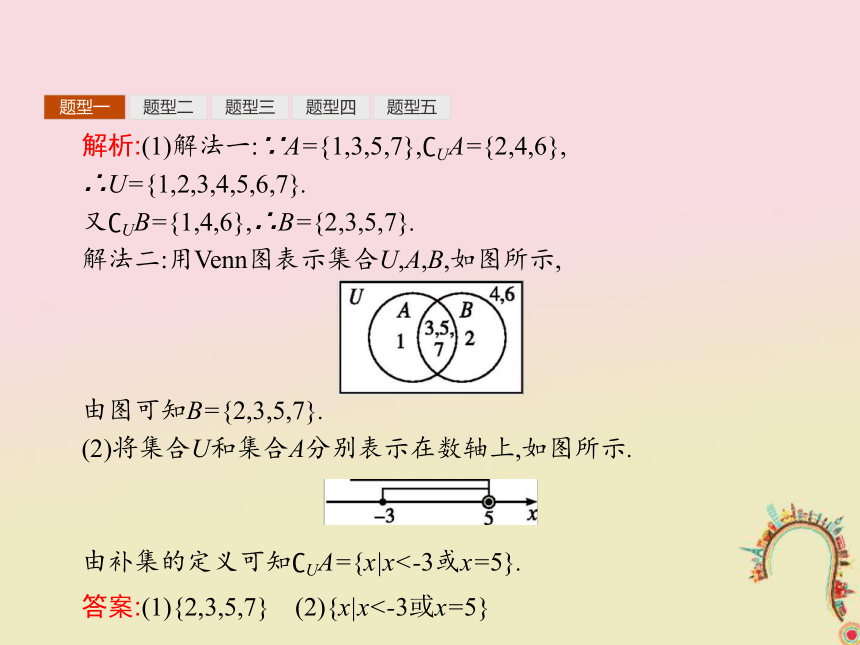
(2)利用补集的定义,借助于数轴的直观作用求解.题型一题型二题型三题型四题型五解析:(1)解法一:∵A={1,3,5,7},?UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又?UB={1,4,6},∴B={2,3,5,7}.
解法二:用Venn图表示集合U,A,B,如图所示,
由图可知B={2,3,5,7}.
(2)将集合U和集合A分别表示在数轴上,如图所示.
由补集的定义可知?UA={x|x<-3或x=5}.答案:(1){2,3,5,7} (2){x|x<-3或x=5} 题型一题型二题型三题型四题型五【变式训练1】 已知全集U={x|-5≤x≤2},集合A={x|0≤x<1},则?UA= .?
解析:将集合U和集合A分别表示在数轴上,如图所示.
由补集定义得?UA={x|-5≤x<0,或1≤x≤2}.
答案:{x|-5≤x<0,或1≤x≤2}题型一题型二题型三题型四题型五交集、并集、补集的综合运算
【例2】 已知全集U={x|x≤4},集合A={x|-2分析:利用数轴分别表示出全集U及集合A,B.先求出?UA及?UB,再求解.
解:将集合U,A,B分别表示在数轴上,如图.所以?UA={x|x≤-2或3≤x≤4}.
?UB={x|x<-3或2所以A∩B={x|-2(?UA)∪B={x|x≤2或3≤x≤4},
A∩(?UB)={x|2A.{5,8} B.{7,9} C.{0,1,3} D.{2,4,6}
(2)设集合S={x|x>-2},T={x|-4≤x≤1},则(?RS)∪T等于( )
A.{x|-2C.{x|x≤1} D.{x|x≥1}
解析:(1)由已知可得?UA={2,4,6,7,9},?UB={0,1,3,7,9},
所以(?UA)∩(?UB)={7,9}.
(2)因为S={x|x>-2},所以?RS={x|x≤-2}.
而T={x|-4≤x≤1},
所以(?RS)∪T={x|x≤-2}∪{x|-4≤x≤1}={x|x≤1}.
答案:(1)B (2)C题型一题型二题型三题型四题型五【例3】 某班共有30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,求喜爱篮球运动但不喜爱乒乓球运动的人数.
分析:先将文字语言转化为集合语言,设U为全班学生组成的集合,A,B分别表示喜爱篮球运动的学生组成的集合、喜爱乒乓球运动的学生组成的集合,再利用Venn图可直观得出答案.有关集合的实际应用题题型一题型二题型三题型四题型五解:设全集U={全班30名学生},A={喜爱篮球运动的学生},B={喜爱乒乓球运动的学生},画出Venn图如图所示.
设既喜爱篮球运动又喜爱乒乓球运动的人数为x,则喜爱篮球运动但不喜爱乒乓球运动的人数为15-x,喜爱乒乓球运动但不喜爱篮球运动的人数为10-x,则有(15-x)+x+(10-x)+8=30,解得x=3.所以喜爱篮球运动但不喜爱乒乓球运动的人数为15-x=15-3=12.
反思解答有关集合的实际应用题时,首先要将文字语言转化为集合语言,然后结合集合的交、并、补运算来处理.此外,由于Venn图简明、直观,很多有关集合的实际应用问题往往借助Venn图来分析.题型一题型二题型三题型四题型五【变式训练3】 某商店销售电视机和电脑两种电器,有15人进入该商店,有6人买了电视机,有5人买了电脑,其中有2人同时买了电视机和电脑,求这15人中没有在该商店消费的人数.
解:设全集U={进入商店的15人},A={买电视机的顾客},B={买电脑的顾客},画出Venn图,如图所示,则A∩B中有2人,(?UA)∩B中有5-2=3(人),(?UB)∩A中有6-2=4(人),则?U(A∪B)中有15-4-2-3=6(人),即这15人中没有在该商店消费的人数是6.题型一题型二题型三题型四题型五由集合的补集关系求参数的值(范围)
【例4】 设集合A={x|x+m≥0},B={x|-2分析:(?UA)∩B=?说明两个非空集合?UA和B没有公共元素.
解:易得A={x|x≥-m},所以?UA={x|x<-m}.又B={x|-2(1)有限集,由补集求参数问题,若集合中元素个数有限时,可利用补集定义并结合集合知识求解.
(2)无限集,与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,则一般利用数轴分析法求解.题型一题型二题型三题型四题型五【变式训练4】 若将例4中条件“(?UA)∩B=?”改为“(?UB)∪A=R”,其他条件不变,求m的取值范围.
解:由已知可得A={x|x≥-m},?UB={x|x≤-2,或x≥4}.
因为(?UB)∪A=R,所以-m≤-2,解得m≥2.题型一题型二题型三题型四题型五易混易错题
易错点 求补集时易漏掉一些特殊元素
【例5】 已知R为全集,A={x|-1≤x<3},B={x|-2错解∵A={x|-1≤x<3},
∴?RA={x|x<-1或x>3}.
∵B={x|-2∴(?RA)∩B={x|-2错因分析:错解在求A的补集时,由于考虑不严密,漏掉了元素3,从而导致最后的结果是错误的.题型一题型二题型三题型四题型五正解:∵A={x|-1≤x<3},
∴?RA={x|x<-1或x≥3}.
∵B={x|-2∴(?RA)∩B={x|-2反思已知集合是“连续”的数集(如本题中的集合A,B),求其补集时,易漏掉一些特殊的数(如端点等),可借助数轴来解决.题型一题型二题型三题型四题型五【变式训练5】 设全集U={2,3,a2+2a-3},A={|2a-1|,2},?UA={5},求实数a的值.
解法一:∵?UA={5},
∴5∈U,且5?A,
∴a2+2a-3=5,且|2a-1|≠5,
解得a=2或a=-4.
当a=2时,|2a-1|=3,A={2,3},符合题意;而当a=-4时,A={9,2},不是U的子集.∴a=2.
解法二:∵?UA={5},∴5∈U,且5?A,且|2a-1|=3.
2.能够解决交集、并集、补集的综合运算问题.
3.能借助Venn图,利用集合运算解决有关的实际应用问题.1.全集 2.补集 归纳总结1.简单地说,?UA是从全集U中取出集合A的全部元素之后,所有剩余的元素组成的集合.
2.性质:A∪(?UA)=U,A∩(?UA)=?,?U(?UA)=A,?UU=?,?U?=U,?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
3.如图,阴影部分是常用到的含有两个集合运算结果的Venn图表示.【做一做1】 设全集U={1,2,4,8},M={1,2},则?UM等于( )
A.{4} B.{8} C.{4,8} D.?
答案:C
【做一做2】 已知全集U=R,集合A={x|2
可知?UA={x|x≤2或x>5}.
答案:{x|x≤2或x>5}?AC与?BC不一定相等
剖析依据补集的含义,符号?AC和?BC都表示集合C的补集,但是?AC表示集合C在全集A中的补集,而?BC表示集合C在全集B中的补集;因为集合A和B不一定相等,所以?AC与?BC不一定相等.因此,求集合的补集时,首先要明确全集,否则容易出错.如若集合A={1,2,3,4,5,6,7,8,9},B={0,1,2,3,4},C={1,3,4},则?AC={2,5,6,7,8,9},?BC={0,2},很明显?AC≠?BC.题型一题型二题型三题型四题型五补集运算问题
【例1】 (1)已知全集U,集合A={1,3,5,7},?UA={2,4,6},?UB={1,4,6},则集合B= .?
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则?UA= .?
分析:(1)由A及?UA求出全集U,再由补集定义求出集合B,或利用Venn图求出集合B.
(2)利用补集的定义,借助于数轴的直观作用求解.题型一题型二题型三题型四题型五解析:(1)解法一:∵A={1,3,5,7},?UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又?UB={1,4,6},∴B={2,3,5,7}.
解法二:用Venn图表示集合U,A,B,如图所示,
由图可知B={2,3,5,7}.
(2)将集合U和集合A分别表示在数轴上,如图所示.
由补集的定义可知?UA={x|x<-3或x=5}.答案:(1){2,3,5,7} (2){x|x<-3或x=5} 题型一题型二题型三题型四题型五【变式训练1】 已知全集U={x|-5≤x≤2},集合A={x|0≤x<1},则?UA= .?
解析:将集合U和集合A分别表示在数轴上,如图所示.
由补集定义得?UA={x|-5≤x<0,或1≤x≤2}.
答案:{x|-5≤x<0,或1≤x≤2}题型一题型二题型三题型四题型五交集、并集、补集的综合运算
【例2】 已知全集U={x|x≤4},集合A={x|-2
解:将集合U,A,B分别表示在数轴上,如图.所以?UA={x|x≤-2或3≤x≤4}.
?UB={x|x<-3或2
A∩(?UB)={x|2
(2)设集合S={x|x>-2},T={x|-4≤x≤1},则(?RS)∪T等于( )
A.{x|-2
解析:(1)由已知可得?UA={2,4,6,7,9},?UB={0,1,3,7,9},
所以(?UA)∩(?UB)={7,9}.
(2)因为S={x|x>-2},所以?RS={x|x≤-2}.
而T={x|-4≤x≤1},
所以(?RS)∪T={x|x≤-2}∪{x|-4≤x≤1}={x|x≤1}.
答案:(1)B (2)C题型一题型二题型三题型四题型五【例3】 某班共有30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,求喜爱篮球运动但不喜爱乒乓球运动的人数.
分析:先将文字语言转化为集合语言,设U为全班学生组成的集合,A,B分别表示喜爱篮球运动的学生组成的集合、喜爱乒乓球运动的学生组成的集合,再利用Venn图可直观得出答案.有关集合的实际应用题题型一题型二题型三题型四题型五解:设全集U={全班30名学生},A={喜爱篮球运动的学生},B={喜爱乒乓球运动的学生},画出Venn图如图所示.
设既喜爱篮球运动又喜爱乒乓球运动的人数为x,则喜爱篮球运动但不喜爱乒乓球运动的人数为15-x,喜爱乒乓球运动但不喜爱篮球运动的人数为10-x,则有(15-x)+x+(10-x)+8=30,解得x=3.所以喜爱篮球运动但不喜爱乒乓球运动的人数为15-x=15-3=12.
反思解答有关集合的实际应用题时,首先要将文字语言转化为集合语言,然后结合集合的交、并、补运算来处理.此外,由于Venn图简明、直观,很多有关集合的实际应用问题往往借助Venn图来分析.题型一题型二题型三题型四题型五【变式训练3】 某商店销售电视机和电脑两种电器,有15人进入该商店,有6人买了电视机,有5人买了电脑,其中有2人同时买了电视机和电脑,求这15人中没有在该商店消费的人数.
解:设全集U={进入商店的15人},A={买电视机的顾客},B={买电脑的顾客},画出Venn图,如图所示,则A∩B中有2人,(?UA)∩B中有5-2=3(人),(?UB)∩A中有6-2=4(人),则?U(A∪B)中有15-4-2-3=6(人),即这15人中没有在该商店消费的人数是6.题型一题型二题型三题型四题型五由集合的补集关系求参数的值(范围)
【例4】 设集合A={x|x+m≥0},B={x|-2
解:易得A={x|x≥-m},所以?UA={x|x<-m}.又B={x|-2
(2)无限集,与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,则一般利用数轴分析法求解.题型一题型二题型三题型四题型五【变式训练4】 若将例4中条件“(?UA)∩B=?”改为“(?UB)∪A=R”,其他条件不变,求m的取值范围.
解:由已知可得A={x|x≥-m},?UB={x|x≤-2,或x≥4}.
因为(?UB)∪A=R,所以-m≤-2,解得m≥2.题型一题型二题型三题型四题型五易混易错题
易错点 求补集时易漏掉一些特殊元素
【例5】 已知R为全集,A={x|-1≤x<3},B={x|-2
∴?RA={x|x<-1或x>3}.
∵B={x|-2
∴?RA={x|x<-1或x≥3}.
∵B={x|-2
解法一:∵?UA={5},
∴5∈U,且5?A,
∴a2+2a-3=5,且|2a-1|≠5,
解得a=2或a=-4.
当a=2时,|2a-1|=3,A={2,3},符合题意;而当a=-4时,A={9,2},不是U的子集.∴a=2.
解法二:∵?UA={5},∴5∈U,且5?A,且|2a-1|=3.
