2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.2.1函数的概念(33张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.2.1函数的概念(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 875.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览











文档简介
课件33张PPT。1.2 函数及其表示1.2.1 函数的概念1.能够用集合与对应的语言给出函数的定义;知道构成函数的要素,清楚函数的定义中“任意一个数x ”和“唯一确定的数f(x)”的含义;明确符号“f(x)”表示的意义.
2.会判断两个函数是否相等;会求简单函数的函数值(或值域)和定义域.
3.能正确使用区间表示数集.1.函数的概念
设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.其中x叫做自变量,x的取值范围A叫做函数y=f(x)的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数y=f(x)的值域,则值域是集合B的子集.名师点拨1.“A,B是非空的数集”,一方面强调了A,B只能是数集,即A,B中的元素只能是实数;另一方面指出了定义域、值域都不能是空集,也就是说,定义域为空集的函数是不存在的.
2.函数定义中强调“三性”:任意性、存在性、唯一性,即对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三个性质只要有一个不满足便不能构成函数.
3.理解函数的概念要注意,函数的定义域是非空数集A,但函数的值域不一定是非空数集B,而是集合B的子集.【做一做1】 下列对应关系是从A到B的函数的是 ( )
A.A∈R,B∈R,x2+y2=1
B.A={1,2,3,4},B={0,1},对应关系如图:值不唯一,故不符合;对于B项,符合函数的定义;对于C项,2∈A,但在集合B中找不到相对应的数,故不符合;对于D项,-1∈A,但在集合B中找不到相对应的数,故不符合.
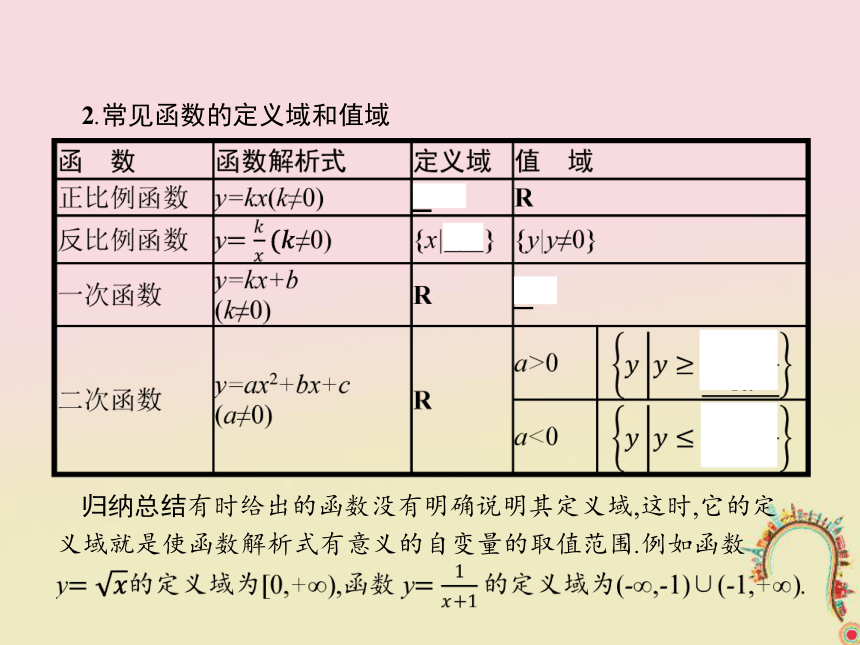
答案:B2.常见函数的定义域和值域 归纳总结有时给出的函数没有明确说明其定义域,这时,它的定义域就是使函数解析式有意义的自变量的取值范围.例如函数【做一做2-1】 已知函数y=f(x)的定义域为P,值域为Q,对于m∈P,与m对应的函数值为n,则有( )
A.n∈P
B.m=n
C.n∈P∩Q
D.n唯一
答案:D
【做一做2-2】 函数y=5-2x的定义域是( )
A.R B.Q
C.N D.?
答案:A【做一做2-3】 函数y=2x2-x的值域是 .?
解析:函数y=2x2-x是二次函数,其二次项系数大于零,3.区间与无穷大
(1)区间的概念.
设a,b是两个实数,且a这里的实数a与b都叫做相应区间的端点.知识拓展1.区间符号里面的两个字母(或数字)之间用“,”隔开;
2.区间表示实数集的几条原则:连续的数集,左端点必须小于右端点,开或闭不能混淆;
3.用数轴表示区间时,要特别注意实心点与空心圆圈的区别;
4.由于区间是表示数集的一种形式,因此对于集合的运算仍然成立.(2)无穷大.
“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”,满足x≥a,x>a,x≤a,xA.(-∞,1) B.(-∞,1]
C.(1,+∞) D.[1,+∞)
答案:D
【做一做3-2】 区间[5,8)表示的集合是( )
A.{x|x≤5,或x>8} B.{x|5C.{x|5≤x<8} D.{x|5≤x≤8}
答案:C名师点拨1.∞是一个符号,而不是一个数;
2.当以“-∞”或“+∞”为区间的一端时,这一端必须用小括号.4.函数相等
一个函数的构成要素为:定义域、对应关系和值域,其中值域是由定义域和对应关系决定的.如果两个函数的定义域相同,并且对应关系完全一致,我们就称这两个函数相等.【做一做4】 在下列函数中,与函数y=2x2表示同一函数的是( )解析:A选项,y=2x与函数y=2x2的对应关系不同,所以它们不表示同一函数;
B选项,y=2t2,其定义域、对应关系与函数y=2x2均相同,所以它们表示同一函数;答案:B 函数符号f(x)的意义
剖析(1)符号y=f(x)表示因变量y是自变量x的函数,它仅仅是函数符号,并不表示y等于f与x的乘积.
(2)符号f(x)与f(m)既有区别又有联系,当m是变量时,函数f(x)与函数f(m)相等;当m是常数时,f(m)表示当自变量x=m时对应的函数值,是一个常量.
(3)符号f可以看作是对“x”施加的某种法则或运算.
例如f(x)=x2-x+5,当x=2时,看作对“2”施加了这样的运算法则:先平方,再减去2,最后加上5;当x为某一代数式(或某一个函数)时,则左右两边的所有x都用同一个代数式(或某一个函数)来代替.如:f(2x+1)=(2x+1)2-(2x+1)+5,f(g(x))=[g(x)]2-g(x)+5.题型一题型二题型三题型四题型五函数关系的判断
【例1】 下列式子能否确定y是x的函数?分析:先将已知式子进行等价转换,化为用x表示y的形式,再利用函数的定义进行判断.题型一题型二题型三题型四题型五所以当x在{x|x≥1}中任取一个值时,都有唯一的y值与之对应,故y是x的函数.所以y不是x的函数.
反思1.判断一个对应关系f:A→B是不是函数,要从以下三个方面去判断:(1)A,B必须是非空数集;(2)A中的任何一个元素在B中必须有元素与其对应;(3)A中任一元素在B中必有唯一元素与其对应.
2.函数的定义中“任意一个数x”与“唯一确定的数f(x)”说明函数中两个变量x,y的对应关系是“一对一”或者是“多对一”,而不能是“一对多 ”.题型一题型二题型三题型四题型五【变式训练1】 设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形:
其中,能表示从集合M到集合N的函数关系的个数是 ( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四题型五解析:①中,因为在集合M中当1答案:B题型一题型二题型三题型四题型五求函数的定义域分析:分析所给函数表达式→列不等式组→求x的范围,得定义域解得x≤1,且x≠-1,
即函数的定义域是{x|x≤1,且x≠-1}.题型一题型二题型三题型四题型五反思1.如果f(x)是整式,那么函数f(x)的定义域是实数集R.
2.如果f(x)是分式,那么函数f(x)的定义域是使分母不等于零的实数的集合.
3.如果f(x)是二次根式,那么函数f(x)的定义域是使根号内的式子大于或等于零的实数的集合.
4.如果f(x)是由几个部分构成的,那么函数f(x)的定义域是使各部分式子都有意义的实数的集合(即求各部分自变量取值集合的交集).
5.对于由实际背景确定的函数,其定义域还要受实际问题的制约.题型一题型二题型三题型四题型五【变式训练2】 求下列函数的定义域: 故原函数的定义域为{x|x<0,且x≠-1}. 题型一题型二题型三题型四题型五求函数值(值域)(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)求g(x)的值域.
分析:(1)分别将f(x)与g(x)的表达式中的x换为2,计算得f(2)与g(2)的值;(2)先求g(3)的值m,再求f(m)的值;(3)g(x)的所有函数值构成的集合即为g(x)的值域.题型一题型二题型三题型四题型五(2)∵g(3)=32+2=11, (3)∵x∈R,∴x2+2≥2.∴g(x)的值域为[2,+∞).
反思已知f(x)的解析式时,只需用a替换解析式中的x即得f(a)的值;已知g(x)的解析式时,先求g(a)的值m,再求f(m)的值即得f(g(a))的值,即遵循由里往外的原则求f(g(a)).题型一题型二题型三题型四题型五【变式训练3】 (1)已知f(x)=2x+1,g(x)=x2+1,若f(2a+1)=7,则f(g(a))= ;?
(2)函数y=x+1,x∈{1,2,3,4}的值域为 .?
解析:(1)∵f(x)=2x+1,∴f(2a+1)=2(2a+1)+1=4a+3=7,
∴a=1.∴g(a)=a2+1=2,
∴f(g(a))=f(2)=2×2+1=5.
(2) ∵x∈{1,2,3,4},分别代入y=x+1求值,
可得所求函数值域为{2,3,4,5}.
答案:(1)5 (2){2,3,4,5}题型一题型二题型三题型四题型五判断函数相等
【例4】 判断下列各组函数是不是相等函数:(2)f(x)=(x-1)2,g(x)=x-1;
(3)f(x)=x2+x+1,g(t)=t2+t+1.
分析:先求出函数定义域,再根据定义域和对应关系来确定.
解:(1)f(x)的定义域为R,g(x)的定义域为{x|x≠2}.
由于定义域不同,故f(x)与g(x)不是相等函数.
(2)f(x)的定义域为R,g(x)的定义域为R,即定义域相同.由于f(x)与g(x)的表达式不相同,即对应关系不一致,故f(x)与g(x)不是相等函数.
(3)两个函数的自变量所用字母不同,但其定义域相同,且对应关系一致,故两个函数相等.题型一题型二题型三题型四题型五反思判断两个函数f(x)和g(x)是否相等的方法是:求函数f(x)和g(x)的定义域,如果定义域不同,那么它们不相等;如果定义域相同,那么化简函数的解析式;如果化简后的函数解析式相同,那么它们相等,否则它们不相等.题型一题型二题型三题型四题型五【变式训练4】 试判断以下各组函数是否表示同一函数:题型一题型二题型三题型四题型五(3)由于y=x0要求x≠0,且当x≠0时,y=x0=1,故y=x0与y=1(x≠0)的定义域和对应关系都相同,所以它们表示同一函数.题型一题型二题型三题型四题型五易混易错题
易错点 求函数的定义域时,先化简函数的解析式需x≠-3.故所求函数的定义域为{x|x≠-3}.
错因分析:约分扩大了自变量的取值范围.同时约去了函数中分题型一题型二题型三题型四题型五正解:要使函数有意义,必须使(x-2)(x+3)≠0,
即x-2≠0,且x+3≠0,解得x≠2,且x≠-3,
故所求函数的定义域为{x|x≠2,且x≠-3}.题型一题型二题型三题型四题型五【变式训练5】 已知下列说法: A.0 B.1 C.2 D.3 的定义域为{x|x≠-2},故②不正确;③当x=-1时,函数值y=2,故③不正确.
答案:A
2.会判断两个函数是否相等;会求简单函数的函数值(或值域)和定义域.
3.能正确使用区间表示数集.1.函数的概念
设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.其中x叫做自变量,x的取值范围A叫做函数y=f(x)的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数y=f(x)的值域,则值域是集合B的子集.名师点拨1.“A,B是非空的数集”,一方面强调了A,B只能是数集,即A,B中的元素只能是实数;另一方面指出了定义域、值域都不能是空集,也就是说,定义域为空集的函数是不存在的.
2.函数定义中强调“三性”:任意性、存在性、唯一性,即对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三个性质只要有一个不满足便不能构成函数.
3.理解函数的概念要注意,函数的定义域是非空数集A,但函数的值域不一定是非空数集B,而是集合B的子集.【做一做1】 下列对应关系是从A到B的函数的是 ( )
A.A∈R,B∈R,x2+y2=1
B.A={1,2,3,4},B={0,1},对应关系如图:值不唯一,故不符合;对于B项,符合函数的定义;对于C项,2∈A,但在集合B中找不到相对应的数,故不符合;对于D项,-1∈A,但在集合B中找不到相对应的数,故不符合.
答案:B2.常见函数的定义域和值域 归纳总结有时给出的函数没有明确说明其定义域,这时,它的定义域就是使函数解析式有意义的自变量的取值范围.例如函数【做一做2-1】 已知函数y=f(x)的定义域为P,值域为Q,对于m∈P,与m对应的函数值为n,则有( )
A.n∈P
B.m=n
C.n∈P∩Q
D.n唯一
答案:D
【做一做2-2】 函数y=5-2x的定义域是( )
A.R B.Q
C.N D.?
答案:A【做一做2-3】 函数y=2x2-x的值域是 .?
解析:函数y=2x2-x是二次函数,其二次项系数大于零,3.区间与无穷大
(1)区间的概念.
设a,b是两个实数,且a
2.区间表示实数集的几条原则:连续的数集,左端点必须小于右端点,开或闭不能混淆;
3.用数轴表示区间时,要特别注意实心点与空心圆圈的区别;
4.由于区间是表示数集的一种形式,因此对于集合的运算仍然成立.(2)无穷大.
“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”,满足x≥a,x>a,x≤a,x
C.(1,+∞) D.[1,+∞)
答案:D
【做一做3-2】 区间[5,8)表示的集合是( )
A.{x|x≤5,或x>8} B.{x|5
答案:C名师点拨1.∞是一个符号,而不是一个数;
2.当以“-∞”或“+∞”为区间的一端时,这一端必须用小括号.4.函数相等
一个函数的构成要素为:定义域、对应关系和值域,其中值域是由定义域和对应关系决定的.如果两个函数的定义域相同,并且对应关系完全一致,我们就称这两个函数相等.【做一做4】 在下列函数中,与函数y=2x2表示同一函数的是( )解析:A选项,y=2x与函数y=2x2的对应关系不同,所以它们不表示同一函数;
B选项,y=2t2,其定义域、对应关系与函数y=2x2均相同,所以它们表示同一函数;答案:B 函数符号f(x)的意义
剖析(1)符号y=f(x)表示因变量y是自变量x的函数,它仅仅是函数符号,并不表示y等于f与x的乘积.
(2)符号f(x)与f(m)既有区别又有联系,当m是变量时,函数f(x)与函数f(m)相等;当m是常数时,f(m)表示当自变量x=m时对应的函数值,是一个常量.
(3)符号f可以看作是对“x”施加的某种法则或运算.
例如f(x)=x2-x+5,当x=2时,看作对“2”施加了这样的运算法则:先平方,再减去2,最后加上5;当x为某一代数式(或某一个函数)时,则左右两边的所有x都用同一个代数式(或某一个函数)来代替.如:f(2x+1)=(2x+1)2-(2x+1)+5,f(g(x))=[g(x)]2-g(x)+5.题型一题型二题型三题型四题型五函数关系的判断
【例1】 下列式子能否确定y是x的函数?分析:先将已知式子进行等价转换,化为用x表示y的形式,再利用函数的定义进行判断.题型一题型二题型三题型四题型五所以当x在{x|x≥1}中任取一个值时,都有唯一的y值与之对应,故y是x的函数.所以y不是x的函数.
反思1.判断一个对应关系f:A→B是不是函数,要从以下三个方面去判断:(1)A,B必须是非空数集;(2)A中的任何一个元素在B中必须有元素与其对应;(3)A中任一元素在B中必有唯一元素与其对应.
2.函数的定义中“任意一个数x”与“唯一确定的数f(x)”说明函数中两个变量x,y的对应关系是“一对一”或者是“多对一”,而不能是“一对多 ”.题型一题型二题型三题型四题型五【变式训练1】 设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形:
其中,能表示从集合M到集合N的函数关系的个数是 ( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四题型五解析:①中,因为在集合M中当1
即函数的定义域是{x|x≤1,且x≠-1}.题型一题型二题型三题型四题型五反思1.如果f(x)是整式,那么函数f(x)的定义域是实数集R.
2.如果f(x)是分式,那么函数f(x)的定义域是使分母不等于零的实数的集合.
3.如果f(x)是二次根式,那么函数f(x)的定义域是使根号内的式子大于或等于零的实数的集合.
4.如果f(x)是由几个部分构成的,那么函数f(x)的定义域是使各部分式子都有意义的实数的集合(即求各部分自变量取值集合的交集).
5.对于由实际背景确定的函数,其定义域还要受实际问题的制约.题型一题型二题型三题型四题型五【变式训练2】 求下列函数的定义域: 故原函数的定义域为{x|x<0,且x≠-1}. 题型一题型二题型三题型四题型五求函数值(值域)(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)求g(x)的值域.
分析:(1)分别将f(x)与g(x)的表达式中的x换为2,计算得f(2)与g(2)的值;(2)先求g(3)的值m,再求f(m)的值;(3)g(x)的所有函数值构成的集合即为g(x)的值域.题型一题型二题型三题型四题型五(2)∵g(3)=32+2=11, (3)∵x∈R,∴x2+2≥2.∴g(x)的值域为[2,+∞).
反思已知f(x)的解析式时,只需用a替换解析式中的x即得f(a)的值;已知g(x)的解析式时,先求g(a)的值m,再求f(m)的值即得f(g(a))的值,即遵循由里往外的原则求f(g(a)).题型一题型二题型三题型四题型五【变式训练3】 (1)已知f(x)=2x+1,g(x)=x2+1,若f(2a+1)=7,则f(g(a))= ;?
(2)函数y=x+1,x∈{1,2,3,4}的值域为 .?
解析:(1)∵f(x)=2x+1,∴f(2a+1)=2(2a+1)+1=4a+3=7,
∴a=1.∴g(a)=a2+1=2,
∴f(g(a))=f(2)=2×2+1=5.
(2) ∵x∈{1,2,3,4},分别代入y=x+1求值,
可得所求函数值域为{2,3,4,5}.
答案:(1)5 (2){2,3,4,5}题型一题型二题型三题型四题型五判断函数相等
【例4】 判断下列各组函数是不是相等函数:(2)f(x)=(x-1)2,g(x)=x-1;
(3)f(x)=x2+x+1,g(t)=t2+t+1.
分析:先求出函数定义域,再根据定义域和对应关系来确定.
解:(1)f(x)的定义域为R,g(x)的定义域为{x|x≠2}.
由于定义域不同,故f(x)与g(x)不是相等函数.
(2)f(x)的定义域为R,g(x)的定义域为R,即定义域相同.由于f(x)与g(x)的表达式不相同,即对应关系不一致,故f(x)与g(x)不是相等函数.
(3)两个函数的自变量所用字母不同,但其定义域相同,且对应关系一致,故两个函数相等.题型一题型二题型三题型四题型五反思判断两个函数f(x)和g(x)是否相等的方法是:求函数f(x)和g(x)的定义域,如果定义域不同,那么它们不相等;如果定义域相同,那么化简函数的解析式;如果化简后的函数解析式相同,那么它们相等,否则它们不相等.题型一题型二题型三题型四题型五【变式训练4】 试判断以下各组函数是否表示同一函数:题型一题型二题型三题型四题型五(3)由于y=x0要求x≠0,且当x≠0时,y=x0=1,故y=x0与y=1(x≠0)的定义域和对应关系都相同,所以它们表示同一函数.题型一题型二题型三题型四题型五易混易错题
易错点 求函数的定义域时,先化简函数的解析式需x≠-3.故所求函数的定义域为{x|x≠-3}.
错因分析:约分扩大了自变量的取值范围.同时约去了函数中分题型一题型二题型三题型四题型五正解:要使函数有意义,必须使(x-2)(x+3)≠0,
即x-2≠0,且x+3≠0,解得x≠2,且x≠-3,
故所求函数的定义域为{x|x≠2,且x≠-3}.题型一题型二题型三题型四题型五【变式训练5】 已知下列说法: A.0 B.1 C.2 D.3 的定义域为{x|x≠-2},故②不正确;③当x=-1时,函数值y=2,故③不正确.
答案:A
