2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.3.1单调性与最大小值(第1课时)函数的单调性(24张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.3.1单调性与最大小值(第1课时)函数的单调性(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览







文档简介
课件24张PPT。1.3 函数的基本性质1.3.1 单调性与最大(小)值第1课时 函数的单调性1.理解增函数和减函数的定义,明确定义中“任意”两字的重要性,以及图象的特征.
2.知道函数单调性的含义,能够利用定义证明函数的单调性.
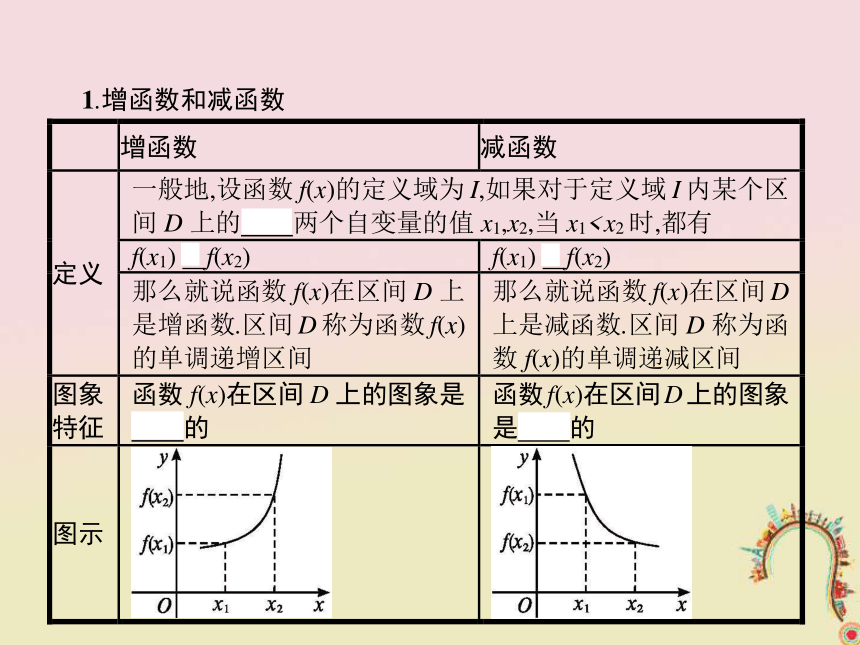
3.能够利用定义或图象求函数的单调区间,能够利用函数的单调性解决有关问题.1.增函数和减函数 【做一做1-1】 已知函数y=f(x)在区间(a,b)内是减函数,x1,x2∈(a,b),且x1A.f(x1)f(x2)
C.f(x1)=f(x2) D.以上都有可能
答案:B
【做一做1-2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)A.是增函数 B.是减函数
C.不是增函数就是减函数 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)答案:D2.单调性
(1)定义:如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在区间D上具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
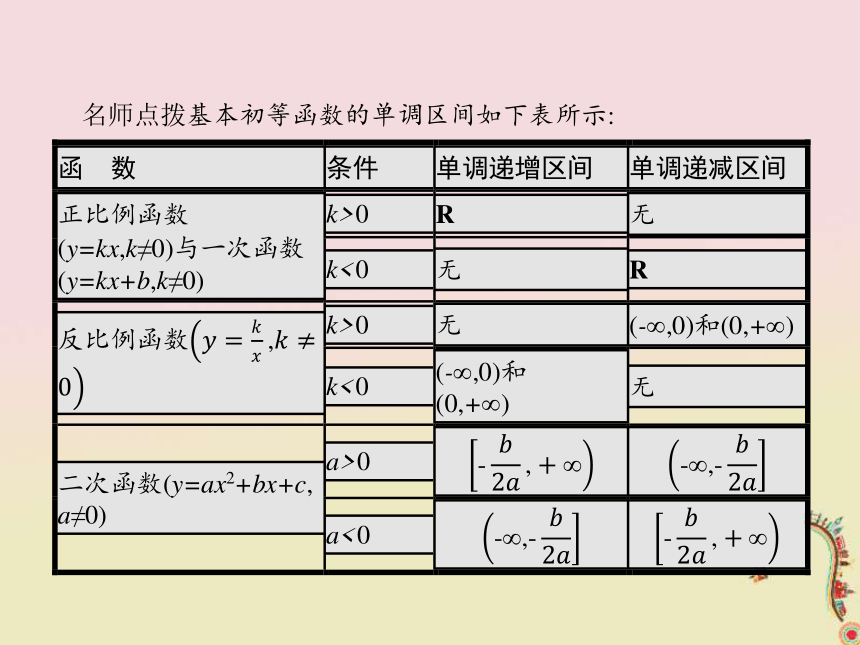
(2)图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.名师点拨基本初等函数的单调区间如下表所示: 【做一做2】 已知函数f(x)的图象如图所示,则( )
A.函数f(x)在区间[-1,2]上是增函数
B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数
D.函数f(x)在区间[2,4]上是增函数
答案:A对函数单调性的理解
剖析函数单调性的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是增函数(减函数),等价于对于D中任意的两个自变量x1,x2,且x1f(x2));其中“任意”二字是关键,不能用具体的两个自函数的单调性是函数定义域内某个区间上的性质,因此它是一个“局部”的性质,并且在考查函数的单调性时,必须先看函数的定义域.如果一个函数有多个单调增(减)区间,这些增(减)区间应用逗号隔开(即“局部”),而不能用并集的符号连接(并完之后就成了“整体”).和(0,+∞)),但不能写成(-∞,0)∪(0,+∞).
因为函数的单调性是反映函数图象变化趋势的,所以在某一点处没法讨论函数的单调性,比如函数y=x2的单调递增区间可以写成开区间(0,+∞),也可以写成[0,+∞),但是若定义域中不包含这个点,则必须使用开区间表示.题型一题型二题型三题型四利用图象确定函数的单调区间
【例1】 已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x);
(2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
分析:(1)需要讨论x≥0和x<0两种情况;(2)利用画分段函数图象的步骤画出;(3)借助函数图象写出单调区间.
解:(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,题型一题型二题型三题型四(2)函数f(x)的图象如图所示.
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,在区间(-1,0)和(1,+∞)内是下降的,所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).2.对于含有绝对值的函数,往往要转化成分段函数,画出其图象,借助图象的变化趋势分析函数的单调性(区间).题型一题型二题型三题型四可知f(x)在区间(-∞,0]和[1,+∞)上都是增函数,在(0,1)上是减函数.
答案:(-∞,0],[1,+∞) (0,1)题型一题型二题型三题型四证明函数的单调性分析:在区间(0,1)内任取x1,x2,且x1f(x2)即可.
证明:设x1,x2是区间(0,1)内的任意两个实数,且x1∴x1x2-1<0,x1-x2<0,x1x2>0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).题型一题型二题型三题型四反思证明函数单调性的常用方法是定义法,利用定义法判断函数单调性的步骤为:题型一题型二题型三题型四【变式训练2】 用单调性的定义证明:函数f(x)=2x2+4x在区间 (-∞,-1]上是减函数.∵x1∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在区间(-∞,-1]上是减函数.题型一题型二题型三题型四函数单调性的应用
【例3】 已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,f(1-m)分析:利用单调性将函数值的大小关系转化为自变量的大小关系,即脱去符号f,转化为关于m的一元一次不等式组,解出m的取值范围.
解:因为f(x)在区间[-2,2]上单调递增,且f(1-m)2.(1)若f(x)在区间D上是增函数,x1,x2是区间D内的任意两个实数,则f(x1)>f(x2)?x1>x2;f(x1)(2)若f(x)在区间D上是减函数,x1,x2是区间D内的任意两个实数,则f(x1)>f(x2)?x1x2.题型一题型二题型三题型四【变式训练3】 已知函数y=f(x)是区间(-∞,+∞)内的增函数,且f(2x-3)>f(5x+6),求实数x的取值范围.
解:由题意知2x-3>5x+6,
解得x<-3.
故实数x的取值范围是(-∞,-3).题型一题型二题型三题型四易混易错题
易错点 对“单调区间是……”和“在区间……上单调……”理解错误
【例4】 已知函数f(x)=x2+2(a-1)x+2.
(1)若函数f(x)的单调递减区间是(-∞,4],则实数a的值(或取值范围)是 ;?
(2)若函数f(x)在区间(-∞,4]上单调递减,则实数a的值(或取值范围)是 .?
错解(1)函数f(x)的图象的对称轴为直线x=1-a.由于函数f(x)的单调递减区间是(-∞,4],因此1-a≥4,即a≤-3.故应填(-∞,-3].
(2)函数f(x)的图象的对称轴为直线x=1-a.由于函数f(x)在区间 (-∞,4]上单调递减,因此1-a=4,即a=-3.故应填-3.题型一题型二题型三题型四错因分析:函数的单调递减区间是I,指的是函数递减的最大范围为区间I.而函数在某一区间上单调递减,则指此区间是相应单调递减区间的子集.错解颠倒了这两种说法的含义,从而导致出错.
正解:(1)因为函数f(x)的单调递减区间是(-∞,4],且函数f(x)图象的对称轴为直线x=1-a,所以有1-a=4,即a=-3.故应填-3.
(2)因为函数f(x)在区间(-∞,4]上单调递减,且函数f(x)图象的对称轴为直线x=1-a,
所以1-a≥4,即a≤-3.故应填(-∞,-3].题型一题型二题型三题型四【变式训练4】 已知函数f(x)=|x+a|在区间(-∞,1]上单调递减,则a的取值范围是( )
A.a≥1
B.0C.a≤-1
D.-1≤a<0
∴f(x)的递减区间为(-∞,-a].
由题意,(-∞,1]?(-∞,-a],
∴-a≥1,∴a≤-1.
答案:C
2.知道函数单调性的含义,能够利用定义证明函数的单调性.
3.能够利用定义或图象求函数的单调区间,能够利用函数的单调性解决有关问题.1.增函数和减函数 【做一做1-1】 已知函数y=f(x)在区间(a,b)内是减函数,x1,x2∈(a,b),且x1
C.f(x1)=f(x2) D.以上都有可能
答案:B
【做一做1-2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)
C.不是增函数就是减函数 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)
(1)定义:如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在区间D上具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
(2)图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.名师点拨基本初等函数的单调区间如下表所示: 【做一做2】 已知函数f(x)的图象如图所示,则( )
A.函数f(x)在区间[-1,2]上是增函数
B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数
D.函数f(x)在区间[2,4]上是增函数
答案:A对函数单调性的理解
剖析函数单调性的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是增函数(减函数),等价于对于D中任意的两个自变量x1,x2,且x1
因为函数的单调性是反映函数图象变化趋势的,所以在某一点处没法讨论函数的单调性,比如函数y=x2的单调递增区间可以写成开区间(0,+∞),也可以写成[0,+∞),但是若定义域中不包含这个点,则必须使用开区间表示.题型一题型二题型三题型四利用图象确定函数的单调区间
【例1】 已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x);
(2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
分析:(1)需要讨论x≥0和x<0两种情况;(2)利用画分段函数图象的步骤画出;(3)借助函数图象写出单调区间.
解:(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,题型一题型二题型三题型四(2)函数f(x)的图象如图所示.
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,在区间(-1,0)和(1,+∞)内是下降的,所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).2.对于含有绝对值的函数,往往要转化成分段函数,画出其图象,借助图象的变化趋势分析函数的单调性(区间).题型一题型二题型三题型四可知f(x)在区间(-∞,0]和[1,+∞)上都是增函数,在(0,1)上是减函数.
答案:(-∞,0],[1,+∞) (0,1)题型一题型二题型三题型四证明函数的单调性分析:在区间(0,1)内任取x1,x2,且x1
证明:设x1,x2是区间(0,1)内的任意两个实数,且x1
∴f(x1)-f(x2)>0,即f(x1)>f(x2).题型一题型二题型三题型四反思证明函数单调性的常用方法是定义法,利用定义法判断函数单调性的步骤为:题型一题型二题型三题型四【变式训练2】 用单调性的定义证明:函数f(x)=2x2+4x在区间 (-∞,-1]上是减函数.∵x1
∴f(x)在区间(-∞,-1]上是减函数.题型一题型二题型三题型四函数单调性的应用
【例3】 已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,f(1-m)
解:因为f(x)在区间[-2,2]上单调递增,且f(1-m)
解:由题意知2x-3>5x+6,
解得x<-3.
故实数x的取值范围是(-∞,-3).题型一题型二题型三题型四易混易错题
易错点 对“单调区间是……”和“在区间……上单调……”理解错误
【例4】 已知函数f(x)=x2+2(a-1)x+2.
(1)若函数f(x)的单调递减区间是(-∞,4],则实数a的值(或取值范围)是 ;?
(2)若函数f(x)在区间(-∞,4]上单调递减,则实数a的值(或取值范围)是 .?
错解(1)函数f(x)的图象的对称轴为直线x=1-a.由于函数f(x)的单调递减区间是(-∞,4],因此1-a≥4,即a≤-3.故应填(-∞,-3].
(2)函数f(x)的图象的对称轴为直线x=1-a.由于函数f(x)在区间 (-∞,4]上单调递减,因此1-a=4,即a=-3.故应填-3.题型一题型二题型三题型四错因分析:函数的单调递减区间是I,指的是函数递减的最大范围为区间I.而函数在某一区间上单调递减,则指此区间是相应单调递减区间的子集.错解颠倒了这两种说法的含义,从而导致出错.
正解:(1)因为函数f(x)的单调递减区间是(-∞,4],且函数f(x)图象的对称轴为直线x=1-a,所以有1-a=4,即a=-3.故应填-3.
(2)因为函数f(x)在区间(-∞,4]上单调递减,且函数f(x)图象的对称轴为直线x=1-a,
所以1-a≥4,即a≤-3.故应填(-∞,-3].题型一题型二题型三题型四【变式训练4】 已知函数f(x)=|x+a|在区间(-∞,1]上单调递减,则a的取值范围是( )
A.a≥1
B.0
D.-1≤a<0
∴f(x)的递减区间为(-∞,-a].
由题意,(-∞,1]?(-∞,-a],
∴-a≥1,∴a≤-1.
答案:C
