2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念本章整合(36张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念本章整合(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览









文档简介
课件36张PPT。本章整合??专题一专题二专题三专题四专题五专题一 判断两个集合间的关系
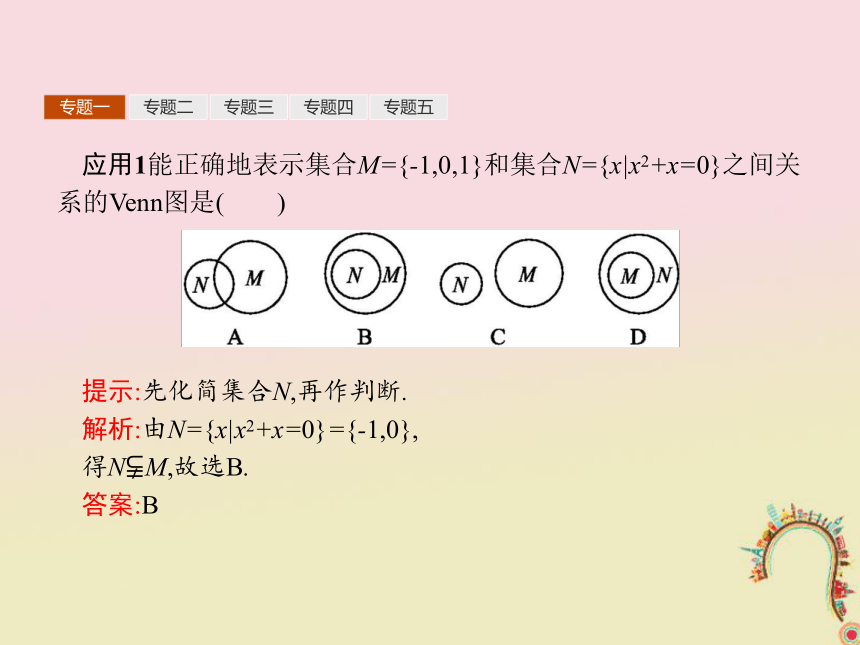
两个集合间的关系可分类如下:集合间的基本关系已经渗透到高中数学的各个章节,特别是与函数、方程、不等式等联系密切.判断两个集合间关系的步骤:(1)首先化简各个集合,明确所给集合中的元素;(2)依据子集、真子集、集合相等的定义来确定两个集合间的关系.专题一专题二专题三专题四专题五应用1能正确地表示集合M={-1,0,1}和集合N={x|x2+x=0}之间关系的Venn图是( )
提示:先化简集合N,再作判断.
解析:由N={x|x2+x=0}={-1,0},
得N?M,故选B.
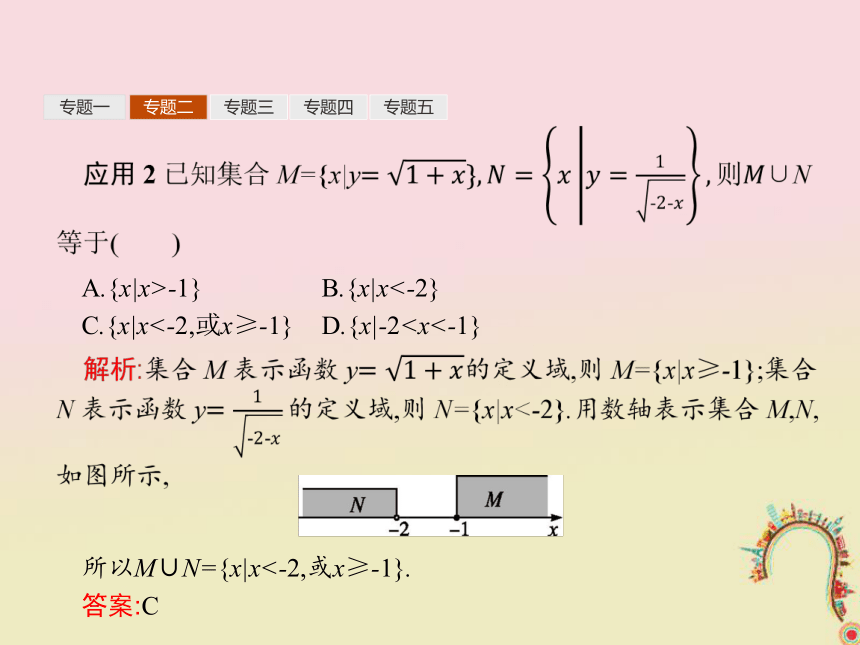
答案:B专题一专题二专题三专题四专题五应用2若集合P={x|y=x2},Q={y|y=x2},则必有 ( )
A.P?Q B.P?Q C.P=Q D.Q?P
提示:与函数y=f(x)有关的集合的含义如下表所示:
解析:集合P是函数y=x2的定义域,则集合P=R;集合Q是函数y=x2的值域,则集合Q={y|y≥0},
所以Q?P.
答案:D专题一专题二专题三专题四专题五专题二 集合的运算
集合的运算主要是指求集合的交集、并集和补集等,在进行集合的运算时,首先要明确元素是什么,全集是什么,保证所有元素都是全集中的元素.根据所给集合的不同表示形式,常常借助于数轴或Venn图进行运算.专题一专题二专题三专题四专题五应用1设集合A={x|x<-2,或x≥3},B={x|0≤x≤4,且x∈Z},则(?RA)∩B等于( )
A.{x|0≤x<3} B.{x|0C.{0,1,2,3} D.{0,1,2}
解析:∵A={x|x<-2,或x≥3},
∴?RA={x|-2≤x<3}.
又B={x|0≤x≤4,且x∈Z},
∴B={0,1,2,3,4}.∴(?RA)∩B={0,1,2}.
答案:D专题一专题二专题三专题四专题五A.{x|x>-1} B.{x|x<-2}
C.{x|x<-2,或x≥-1} D.{x|-2答案:C专题一专题二专题三专题四专题五专题三 求函数最值的方法
函数的最值是函数在整个定义域上的性质,是函数的整体性质,是高考中常见的题型,其常见的求法有直接法、观察法、单调性法、图象法、换元法等.
1.直接法
求反比例函数、一次函数、二次函数的最值时,常利用这些函数的性质和图象,直接写出最值,这种求最值的方法称为直接法.
特别地,求二次函数f(x)=ax2+bx+c(a≠0)在区间[m,n]上的最值时,通常是画出二次函数f(x)=ax2+bx+c在区间[m,n]上的图象,借助函数的图象写出最值,即图象上最高点的纵坐标是函数的最大值,最低点的纵坐标是函数的最小值.专题一专题二专题三专题四专题五应用1函数f(x)=-2x+1在区间[-2,1]上的最大值是 ,最小值是 .?
解析:因为函数f(x)=-2x+1在区间[-2,1]上是减函数,所以最大值是f(-2)=5,最小值是f(1)=-1.
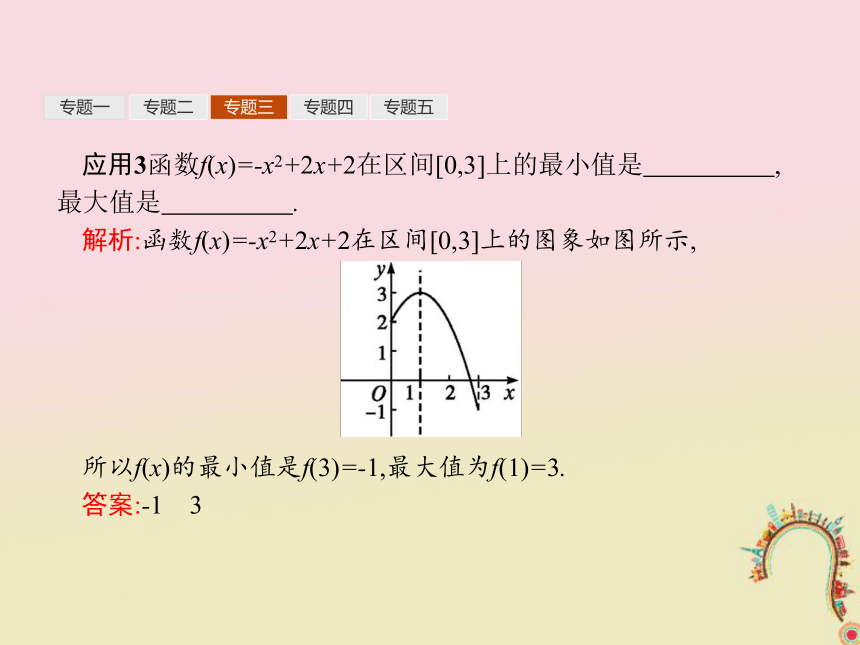
答案:5 -1专题一专题二专题三专题四专题五应用3函数f(x)=-x2+2x+2在区间[0,3]上的最小值是 ,最大值是 .?
解析:函数f(x)=-x2+2x+2在区间[0,3]上的图象如图所示,
所以f(x)的最小值是f(3)=-1,最大值为f(1)=3.
答案:-1 3专题一专题二专题三专题四专题五2.观察法 答案:-2 专题一专题二专题三专题四专题五3.单调性法
若函数f(x)在区间[a,b]上是增函数,则函数f(x)在区间[a,b]上的最大值是f(b),最小值是f(a);若函数f(x)在区间[a,b]上是减函数,则函数f(x)在区间[a,b]上的最大值是f(a),最小值是f(b).专题一专题二专题三专题四专题五(1)判断f(x)在区间[3,5]上的单调性,并加以证明;
(2)求f(x)的最大值和最小值.
解:(1)f(x)在区间[3,5]上单调递增.证明如下:∵x1,x2∈[3,5],
∴x1+1>0,x2+1>0,即(x1+1)(x2+1)>0.
又x1利用图象法求函数f(x)最值的步骤:
(1)画出函数f(x)的图象;
(2)观察图象,找出图象的最高点和最低点;
(3)写出最值,最高点的纵坐标是函数的最大值,最低点的纵坐标是函数的最小值.专题一专题二专题三专题四专题五提示:画出函数的图象,确定图象上的最高点和最低点. 专题一专题二专题三专题四专题五5.换元法 应用1求函数y=x4+2x2-2的最小值.
提示:由于x4的指数是x2的指数的2倍,则可利用换元法转化为求二次函数的最小值.
解:设x2=t,则y=t2+2t-2=(t+1)2-3,t≥0.
∵函数y=(t+1)2-3在[0,+∞)内是增函数,
∴当t=0时,y取最小值-2.
∴函数y=x4+2x2-2的最小值是-2.专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题四 函数的单调性
判断或证明函数f(x)的单调性的方法:
1.定义法
用定义法判断函数f(x)的单调性的步骤是:
(1)在所给区间上任取两个变量x1,x2,且x1(2)比较f(x1)与f(x2)的大小,通常用作差法,先作差,再将差变形,变形的方法有通分、分解因式等,变形应以能够判断差的符号为目的;
(3)归纳结论.
2.图象法
画出函数f(x)的图象,借助图象和函数单调性的几何意义来判断.此法适用于选择题和填空题.专题一专题二专题三专题四专题五解:设x1,x2是区间(1,+∞)内的任意两个实数,且x1∵函数f(x)在区间(1,+∞)内是增函数,∵11,-x1x2<-1.
∴a≥-1,即a的取值范围是[-1,+∞).专题一专题二专题三专题四专题五专题五 函数的奇偶性
判断函数的奇偶性的方法:
1.定义法
用定义法判断函数奇偶性的步骤:先求函数的定义域,当定义域不关于原点对称时,此函数既不是奇函数也不是偶函数;当定义域关于原点对称时,再判断f(-x)与f(x)的关系.
(1)当f(-x)=f(x)时,此函数是偶函数;
(2)当f(-x)=-f(x)时,此函数是奇函数;
(3)当f(-x)=f(x),且f(-x)=-f(x)时,此函数既是奇函数也是偶函数;
(4)当f(-x)≠f(x),且f(-x)≠-f(x)时,此函数既不是奇函数也不是偶函数.专题一专题二专题三专题四专题五2.图象法
画出函数f(x)的图象,依据下列结论写出函数f(x)的奇偶性:如果函数f(x)的图象关于原点对称,那么函数f(x)是奇函数;如果函数f(x)的图象关于y轴对称,那么函数f(x)是偶函数;如果函数f(x)的图象关于原点和y轴均对称,那么函数f(x)既是奇函数也是偶函数;如果函数f(x)的图象关于原点和y轴均不对称,那么函数f(x)既不是奇函数也不是偶函数.专题一专题二专题三专题四专题五解:∵f(x)是奇函数, 专题一专题二专题三专题四专题五应用2已知定义在[-2,2]上的偶函数f(x)在区间[0,2]上是减函数,若f(1-m)提示:应用函数f(x)的奇偶性,将变量1-m和m转化到同一个单调区间[0,2]上,再借助函数的单调性去掉“f”,转化为关于m的不等式组.
解:∵函数f(x)是偶函数,∴f(x)=f(|x|).
∴f(1-m)=f(|1-m|),f(m)=f(|m|).1 2 3 4 5 6 7 8 9 101(2018·全国Ⅰ高考)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}
解析:由交集定义知A∩B={0,2}.
答案:A1 2 3 4 5 6 7 8 9 102(2018·全国Ⅱ高考)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
解析:当x=-1时,y=0或y=1或y=-1,当x=0时,y=1或y=-1或y=0,当x=1时,y=0或y=1或y=-1.故集合A中共有9个元素.
答案:A1 2 3 4 5 6 7 8 9 103(2018·全国Ⅲ高考)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )
A.{0} B.{1} C.{1,2} D.{0,1,2}
解析:由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.
答案:C1 2 3 4 5 6 7 8 9 104(2018·北京高考)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )
A.{0,1} B.{-1,0,1}
C.{-2,0,1,2} D.{-1,0,1,2}
解析:∵|x|<2,∴-2∴A∩B={-2,0,1,2}∩{x|-2答案:A1 2 3 4 5 6 7 8 9 105(2018·天津高考)设全集为R,集合A={x|0A.{x|0C.{x|1≤x<2} D.{x|0解析:∵B={x|x≥1},∴?RB={x|x<1}.
∵A={x|0故选B.
答案:B1 2 3 4 5 6 7 8 9 106(2017·全国Ⅰ高考)已知集合A={x|x<2},B={x|3-2x>0},则( )答案:A 1 2 3 4 5 6 7 8 9 107(2017·全国Ⅱ高考)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A.{1,-3} B.{1,0} C.{1,3} D.{1,5}
解析:由A∩B={1},可知1∈B,所以m=3,即B={1,3},故选C.
答案:C1 2 3 4 5 6 7 8 9 108(2017·全国Ⅲ高考)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1 B.2 C.3 D.4
解析:由题意可得A∩B={2,4},则A∩B中有2个元素.故选B.
答案:B1 2 3 4 5 6 7 8 9 109(2017·全国Ⅰ高考)函数f(x)在区间(-∞,+∞)单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
A.[-2,2] B.[-1,1] C.[0,4] D.[1,3]
解析:因为f(x)为奇函数,所以f(-1)=-f(1)=1,于是-1≤f(x-2)≤1等价于f(1)≤f(x-2)≤f(-1).又f(x)在区间(-∞,+∞)单调递减,所以-1≤x-2≤1,即1≤x≤3.所以x的取值范围是[1,3].
答案:D1 2 3 4 5 6 7 8 9 1010(2017·全国Ⅱ高考)已知函数f(x)是定义在R上的奇函数,当x∈ (-∞,0)时,f(x)=2x3+x2,则f(2)= .?
解析:因为f(x)是奇函数,所以f(-x)=-f(x).
又因为当x∈(-∞,0)时,f(x)=2x3+x2,
所以f(2)=-f(-2)=-[2×(-8)+4]=12.
答案:12
两个集合间的关系可分类如下:集合间的基本关系已经渗透到高中数学的各个章节,特别是与函数、方程、不等式等联系密切.判断两个集合间关系的步骤:(1)首先化简各个集合,明确所给集合中的元素;(2)依据子集、真子集、集合相等的定义来确定两个集合间的关系.专题一专题二专题三专题四专题五应用1能正确地表示集合M={-1,0,1}和集合N={x|x2+x=0}之间关系的Venn图是( )
提示:先化简集合N,再作判断.
解析:由N={x|x2+x=0}={-1,0},
得N?M,故选B.
答案:B专题一专题二专题三专题四专题五应用2若集合P={x|y=x2},Q={y|y=x2},则必有 ( )
A.P?Q B.P?Q C.P=Q D.Q?P
提示:与函数y=f(x)有关的集合的含义如下表所示:
解析:集合P是函数y=x2的定义域,则集合P=R;集合Q是函数y=x2的值域,则集合Q={y|y≥0},
所以Q?P.
答案:D专题一专题二专题三专题四专题五专题二 集合的运算
集合的运算主要是指求集合的交集、并集和补集等,在进行集合的运算时,首先要明确元素是什么,全集是什么,保证所有元素都是全集中的元素.根据所给集合的不同表示形式,常常借助于数轴或Venn图进行运算.专题一专题二专题三专题四专题五应用1设集合A={x|x<-2,或x≥3},B={x|0≤x≤4,且x∈Z},则(?RA)∩B等于( )
A.{x|0≤x<3} B.{x|0
解析:∵A={x|x<-2,或x≥3},
∴?RA={x|-2≤x<3}.
又B={x|0≤x≤4,且x∈Z},
∴B={0,1,2,3,4}.∴(?RA)∩B={0,1,2}.
答案:D专题一专题二专题三专题四专题五A.{x|x>-1} B.{x|x<-2}
C.{x|x<-2,或x≥-1} D.{x|-2
函数的最值是函数在整个定义域上的性质,是函数的整体性质,是高考中常见的题型,其常见的求法有直接法、观察法、单调性法、图象法、换元法等.
1.直接法
求反比例函数、一次函数、二次函数的最值时,常利用这些函数的性质和图象,直接写出最值,这种求最值的方法称为直接法.
特别地,求二次函数f(x)=ax2+bx+c(a≠0)在区间[m,n]上的最值时,通常是画出二次函数f(x)=ax2+bx+c在区间[m,n]上的图象,借助函数的图象写出最值,即图象上最高点的纵坐标是函数的最大值,最低点的纵坐标是函数的最小值.专题一专题二专题三专题四专题五应用1函数f(x)=-2x+1在区间[-2,1]上的最大值是 ,最小值是 .?
解析:因为函数f(x)=-2x+1在区间[-2,1]上是减函数,所以最大值是f(-2)=5,最小值是f(1)=-1.
答案:5 -1专题一专题二专题三专题四专题五应用3函数f(x)=-x2+2x+2在区间[0,3]上的最小值是 ,最大值是 .?
解析:函数f(x)=-x2+2x+2在区间[0,3]上的图象如图所示,
所以f(x)的最小值是f(3)=-1,最大值为f(1)=3.
答案:-1 3专题一专题二专题三专题四专题五2.观察法 答案:-2 专题一专题二专题三专题四专题五3.单调性法
若函数f(x)在区间[a,b]上是增函数,则函数f(x)在区间[a,b]上的最大值是f(b),最小值是f(a);若函数f(x)在区间[a,b]上是减函数,则函数f(x)在区间[a,b]上的最大值是f(a),最小值是f(b).专题一专题二专题三专题四专题五(1)判断f(x)在区间[3,5]上的单调性,并加以证明;
(2)求f(x)的最大值和最小值.
解:(1)f(x)在区间[3,5]上单调递增.证明如下:∵x1,x2∈[3,5],
∴x1+1>0,x2+1>0,即(x1+1)(x2+1)>0.
又x1
(1)画出函数f(x)的图象;
(2)观察图象,找出图象的最高点和最低点;
(3)写出最值,最高点的纵坐标是函数的最大值,最低点的纵坐标是函数的最小值.专题一专题二专题三专题四专题五提示:画出函数的图象,确定图象上的最高点和最低点. 专题一专题二专题三专题四专题五5.换元法 应用1求函数y=x4+2x2-2的最小值.
提示:由于x4的指数是x2的指数的2倍,则可利用换元法转化为求二次函数的最小值.
解:设x2=t,则y=t2+2t-2=(t+1)2-3,t≥0.
∵函数y=(t+1)2-3在[0,+∞)内是增函数,
∴当t=0时,y取最小值-2.
∴函数y=x4+2x2-2的最小值是-2.专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题四 函数的单调性
判断或证明函数f(x)的单调性的方法:
1.定义法
用定义法判断函数f(x)的单调性的步骤是:
(1)在所给区间上任取两个变量x1,x2,且x1
(3)归纳结论.
2.图象法
画出函数f(x)的图象,借助图象和函数单调性的几何意义来判断.此法适用于选择题和填空题.专题一专题二专题三专题四专题五解:设x1,x2是区间(1,+∞)内的任意两个实数,且x1
∴a≥-1,即a的取值范围是[-1,+∞).专题一专题二专题三专题四专题五专题五 函数的奇偶性
判断函数的奇偶性的方法:
1.定义法
用定义法判断函数奇偶性的步骤:先求函数的定义域,当定义域不关于原点对称时,此函数既不是奇函数也不是偶函数;当定义域关于原点对称时,再判断f(-x)与f(x)的关系.
(1)当f(-x)=f(x)时,此函数是偶函数;
(2)当f(-x)=-f(x)时,此函数是奇函数;
(3)当f(-x)=f(x),且f(-x)=-f(x)时,此函数既是奇函数也是偶函数;
(4)当f(-x)≠f(x),且f(-x)≠-f(x)时,此函数既不是奇函数也不是偶函数.专题一专题二专题三专题四专题五2.图象法
画出函数f(x)的图象,依据下列结论写出函数f(x)的奇偶性:如果函数f(x)的图象关于原点对称,那么函数f(x)是奇函数;如果函数f(x)的图象关于y轴对称,那么函数f(x)是偶函数;如果函数f(x)的图象关于原点和y轴均对称,那么函数f(x)既是奇函数也是偶函数;如果函数f(x)的图象关于原点和y轴均不对称,那么函数f(x)既不是奇函数也不是偶函数.专题一专题二专题三专题四专题五解:∵f(x)是奇函数, 专题一专题二专题三专题四专题五应用2已知定义在[-2,2]上的偶函数f(x)在区间[0,2]上是减函数,若f(1-m)
解:∵函数f(x)是偶函数,∴f(x)=f(|x|).
∴f(1-m)=f(|1-m|),f(m)=f(|m|).1 2 3 4 5 6 7 8 9 101(2018·全国Ⅰ高考)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}
解析:由交集定义知A∩B={0,2}.
答案:A1 2 3 4 5 6 7 8 9 102(2018·全国Ⅱ高考)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
解析:当x=-1时,y=0或y=1或y=-1,当x=0时,y=1或y=-1或y=0,当x=1时,y=0或y=1或y=-1.故集合A中共有9个元素.
答案:A1 2 3 4 5 6 7 8 9 103(2018·全国Ⅲ高考)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )
A.{0} B.{1} C.{1,2} D.{0,1,2}
解析:由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.
答案:C1 2 3 4 5 6 7 8 9 104(2018·北京高考)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )
A.{0,1} B.{-1,0,1}
C.{-2,0,1,2} D.{-1,0,1,2}
解析:∵|x|<2,∴-2
∵A={x|0
答案:B1 2 3 4 5 6 7 8 9 106(2017·全国Ⅰ高考)已知集合A={x|x<2},B={x|3-2x>0},则( )答案:A 1 2 3 4 5 6 7 8 9 107(2017·全国Ⅱ高考)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A.{1,-3} B.{1,0} C.{1,3} D.{1,5}
解析:由A∩B={1},可知1∈B,所以m=3,即B={1,3},故选C.
答案:C1 2 3 4 5 6 7 8 9 108(2017·全国Ⅲ高考)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1 B.2 C.3 D.4
解析:由题意可得A∩B={2,4},则A∩B中有2个元素.故选B.
答案:B1 2 3 4 5 6 7 8 9 109(2017·全国Ⅰ高考)函数f(x)在区间(-∞,+∞)单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
A.[-2,2] B.[-1,1] C.[0,4] D.[1,3]
解析:因为f(x)为奇函数,所以f(-1)=-f(1)=1,于是-1≤f(x-2)≤1等价于f(1)≤f(x-2)≤f(-1).又f(x)在区间(-∞,+∞)单调递减,所以-1≤x-2≤1,即1≤x≤3.所以x的取值范围是[1,3].
答案:D1 2 3 4 5 6 7 8 9 1010(2017·全国Ⅱ高考)已知函数f(x)是定义在R上的奇函数,当x∈ (-∞,0)时,f(x)=2x3+x2,则f(2)= .?
解析:因为f(x)是奇函数,所以f(-x)=-f(x).
又因为当x∈(-∞,0)时,f(x)=2x3+x2,
所以f(2)=-f(-2)=-[2×(-8)+4]=12.
答案:12
