2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念函数习题课(26张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念函数习题课(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 653.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览








文档简介
课件26张PPT。函数习题课1.能掌握函数的定义、三要素及其表示.
2.会求函数的定义域、值域、最值.
3.能利用函数单调性、奇偶性的定义研究函数的性质.
4.能解决简单的抽象函数问题.1.函数的三要素:定义域、值域、对应关系.∴函数f(x)的值域为[1,2].
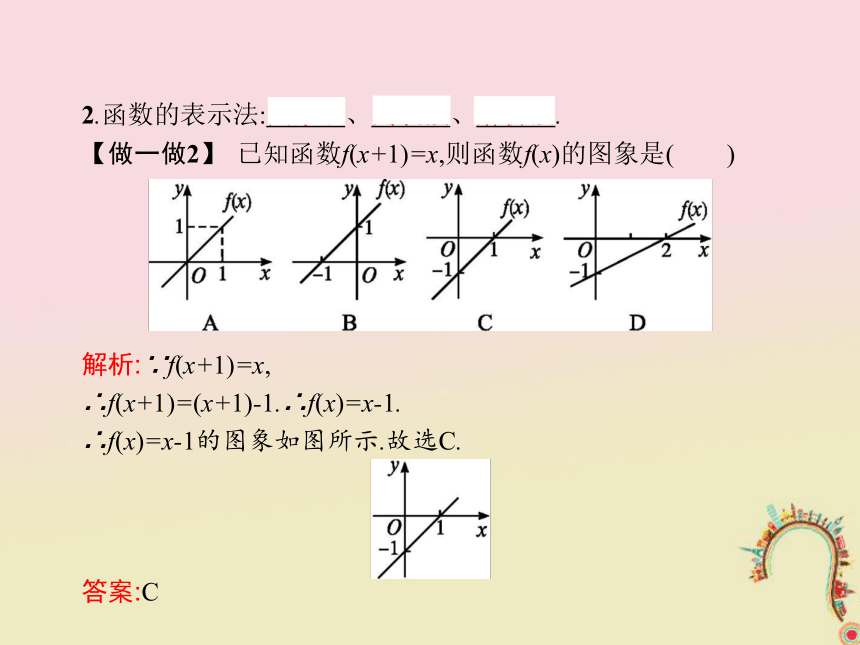
答案:[1,2]2.函数的表示法:图象法、列表法、解析法.
【做一做2】 已知函数f(x+1)=x,则函数f(x)的图象是( )解析:∵f(x+1)=x,
∴f(x+1)=(x+1)-1.∴f(x)=x-1.
∴f(x)=x-1的图象如图所示.故选C.
答案:C3.函数的单调性:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1 f(x2),那么就说函数f(x)在区间D上是减函数.
【做一做3-1】 下列函数在区间(0,+∞)内为增函数的是( )解析:对于B,函数y=x2+2x为二次函数,且图象开口向上,对称轴为x=-1,故函数y=x2+2x在(0,+∞)内为增函数;A,C,D在(0,+∞)内均为减函数.
答案:B【做一做3-2】 已知函数f(x)=|2x-1|,则函数f(x)的递减区间是 .?4.函数的奇偶性:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.
【做一做4】 已知函数f(x)是定义在R上的奇函数.当x<0时,f(x)=-x2+2x,则f(1)= .?
解析:∵当x<0时,f(x)=-x2+2x,
∴f(-1)=-(-1)2+2×(-1)=-3.
又f(x)为奇函数,∴f(1)=-f(-1)=3.
答案:31.利用函数单调性的性质判断函数的单调性
剖析若函数f(x),g(x)在区间D上具有单调性,则在区间D上具有以下性质:
(1)f(x)与-f(x)具有相反的单调性.
(2)f(x)与f(x)+c(c为常数)具有相同的单调性.
(3)当a>0时,f(x)与af(x)具有相同的单调性;当a<0时,f(x)与af(x)具有相反的单调性.(5)当f(x),g(x)都是增(减)函数时,f(x)+g(x)也是增(减)函数.2.函数奇偶性的判断方法
剖析:(1)定义法
根据函数奇偶性的定义进行判断,步骤如下:
①判断函数f(x)的定义域是否关于原点对称.
若不对称,则函数f(x)为非奇非偶函数;若对称,则进行下一步.
②验证.f(-x)=-f(x)或f(-x)=f(x).
③下结论.
若f(-x)=-f(x),则f(x)为奇函数;
若f(-x)=f(x),则f(x)为偶函数;
若f(-x)≠-f(x),且f(-x)≠f(x),则f(x)为非奇非偶函数;若f(-x)=-f(x),且 f(-x)=f(x),则f(x)既是奇函数也是偶函数.(2)图象法
f(x)是奇(偶)函数的条件是f(x)的图象关于原点(y轴)对称.
(3)性质法
①偶函数的和、差、积、商(分母不为零)仍为偶函数;
②奇函数的和、差仍为奇函数;
③奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;
④一个奇函数与一个偶函数的积为奇函数.题型一题型二题型三题型四求函数的定义域和函数值故x=-1或x=3.
答案:(1){x|x≤4,且x≠-1} (2)-1或3题型一题型二题型三题型四反思1.求函数的定义域就是求使函数解析式有意义的自变量的取值集合.如果函数的解析式是由几部分组成,那么它的定义域就是使各部分有意义的自变量的取值集合的交集.
定义域的表示方法与集合的表示方法相同.
2.对于分段函数的函数值,应采用分类讨论思想即分段进行求解.各段独立进行,分别讨论求解.题型一题型二题型三题型四解析:(1)根据题意知g(x)的定义域为B={x|x∵A={x|x≥4},A∩B=?,∴a+1≤4,∴a≤3.
(2)f(7)=f(f(11))=f(8)=f(f(12))=f(9)=6.
答案:(1)a≤3 (2)6题型一题型二题型三题型四求函数的值域
【例2】 (1)函数f(x)=-x2+4x,x∈[0,3)的值域为 ;?解析:(1)(方法1)函数f(x)=-x2+4x为二次函数,图象开口向下,且对称轴为x=2.故当x∈[0,2]时,f(x)单调递增;当x∈(2,3)时,f(x)单调递减.∴当x∈[0,3)时,f(x)max=f(2)=4,f(x)min=f(0)=0.∴f(x)的值域为[0,4].
(方法2)画出函数f(x)=-x2+4x,x∈[0,3)的图象,如图所示,观察图象可得f(x)的值域为[0,4].∴y≠2,故函数值域为{y|y∈R,且y≠2}.
答案:(1)[0,4] (2){y|y∈R,且y≠2}题型一题型二题型三题型四反思求函数值域的方法:
(1)观察法;(2)图象法;(3)单调性法;(4)分离常数法.题型一题型二题型三题型四题型一题型二题型三题型四函数单调性与奇偶性的综合运用
【例3】 (1)已知定义在R上的偶函数f(x)满足:对任意的x1,x2∈ (-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
A.f(-n)B.f(n-1)C.f(n+1)D.f(n+1)(2)已知函数y=f(x)是定义在[-1,1]上的奇函数,又是减函数.若 f(1-a2)+f(1-a)<0,求实数a的取值范围.题型一题型二题型三题型四(1)解析:由(x2-x1)[f(x2)-f(x1)]>0
得f(x)在区间(-∞,0]上为增函数.
∵f(x)为偶函数,
∴f(x)在区间[0,+∞)内为减函数.
又f(-n)=f(n),且0≤n-1∴f(n+1)即f(n+1)答案:C题型一题型二题型三题型四(2)解:由f(1-a2)+f(1-a)<0,
得f(1-a2)<-f(1-a).
∵y=f(x)在区间[-1,1]上是奇函数,
∴-f(1-a)=f(a-1),
∴f(1-a2)又f(x)在定义域[-1,1]上单调递减,∴0≤a<1.∴a的取值范围是[0,1). 题型一题型二题型三题型四反思奇偶性与单调性综合的两种题型及解法
1.比较大小问题,一般解法是先利用奇偶性,将不在同一单调区间上的两个或多个自变量的函数值,转化为其对称区间上的函数值,使其在同一单调区间上,然后利用单调性比较大小.
2.抽象不等式问题,解题步骤是:(1)将所给的不等式转化为两个函数值的大小关系;(2)利用奇偶性得出区间上的单调性,再利用单调性“脱去”函数的符号“f”,转化为解不等式(组)的问题.
需要注意的是:在转化时,自变量的取值必须在同一单调区间上;当不等式一边没有符号“f”时,需转化为含符号“f”的形式,如0=f(1),f(x-1)<0,则f(x-1)A.f(-π)>f(3)>f(-2) B.f(-π)>f(-2)>f(3)
C.f(3)>f(-2)>f(-π) D.f(3)>f(-π)>f(-2)
(2)已知偶函数f(x)在区间[0,+∞)内单调递增,则满足f(2x-1)<题型一题型二题型三题型四解析:(1)∵f(x)是R上的偶函数,
∴f(-2)=f(2),f(-π)=f(π),
又f(x)在区间[0,+∞)上单调递增,且2<3<π,
∴f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2).
(2)由于f(x)为偶函数,且在[0,+∞)上单调递增,答案:(1)A (2)A 题型一题型二题型三题型四抽象函数的单调性与奇偶性问题
【例4】 设函数f(x)对任意x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数.
(2)试问:当-3≤x≤3时,f(x)是否有最值?如果有,求出最值;如果没有,请说明理由.
分析:(1)f(x+y)=f(x)+f(y)对一切x,y∈R均成立,
先计算f(0),再令y=-x,可证得f(x)为奇函数.
(2)利用函数的单调性来确定是否存在最值.题型一题型二题型三题型四解:(1)令x=y=0,
则有f(0+0)=f(0)+f(0),
即f(0)=2f(0),解得f(0)=0.令y=-x,
则有0=f(0)=f(x)+f(-x),故f(x)为奇函数.
(2)任取x1,x2,且-3≤x10.
由题意得f(x2-x1)<0,且
f(x1)-f(x2)=f(x1)-f[x1+(x2-x1)]=f(x1)-[f(x1)+f(x2-x1)]=-f(x2-x1)>0,
即f(x1)>f(x2),∴f(x)在区间[-3,3]上为减函数.
∴f(3)为函数的最小值,f(-3)为函数的最大值.
f(3)=f(1+1+1)=3f(1)=-6,
f(-3)=-f(3)=6,
∴当-3≤x≤3时,函数f(x)的最大值、最小值分别为6,-6.题型一题型二题型三题型四反思抽象函数奇偶性和单调性的判断方法
1.判断或证明抽象函数的奇偶性,需利用奇函数、偶函数的定义,找准方向,巧妙赋值,合理、灵活地变形配凑,找出f(x)与f(-x)的关系.
2.判断或证明抽象函数的单调性,通常有两种方法.
一种是“凑”,凑定义或凑已知,从而使用定义或已知条件得出结论;另一种是“赋值”,给变量赋值要根据条件与结论的关系,有时可能要进行多次尝试.
注意:若给出的是和型(f(x+y)=…)抽象函数,则判定符号时的变形为f(x2)-f(x1)=f((x2-x1)+x1)-f(x1),f(x2)-f(x1)=f(x2)-f((x1-x2)+x2);
若给出的是积型(f(xy)=…)抽象函数,则判定符号时的变形为题型一题型二题型三题型四【变式训练4】 已知函数f(x)的定义域是(0,+∞),当x>1时,f(x)>0,且f(x·y)=f(x)+f(y).
(1)求f(1);
(2)证明:f(x)在定义域上是增函数.
(1)解:令x=y=1,得f(1)=2f(1),故f(1)=0.故f(x)在区间(0,+∞)内是增函数.
2.会求函数的定义域、值域、最值.
3.能利用函数单调性、奇偶性的定义研究函数的性质.
4.能解决简单的抽象函数问题.1.函数的三要素:定义域、值域、对应关系.∴函数f(x)的值域为[1,2].
答案:[1,2]2.函数的表示法:图象法、列表法、解析法.
【做一做2】 已知函数f(x+1)=x,则函数f(x)的图象是( )解析:∵f(x+1)=x,
∴f(x+1)=(x+1)-1.∴f(x)=x-1.
∴f(x)=x-1的图象如图所示.故选C.
答案:C3.函数的单调性:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1
【做一做3-1】 下列函数在区间(0,+∞)内为增函数的是( )解析:对于B,函数y=x2+2x为二次函数,且图象开口向上,对称轴为x=-1,故函数y=x2+2x在(0,+∞)内为增函数;A,C,D在(0,+∞)内均为减函数.
答案:B【做一做3-2】 已知函数f(x)=|2x-1|,则函数f(x)的递减区间是 .?4.函数的奇偶性:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.
【做一做4】 已知函数f(x)是定义在R上的奇函数.当x<0时,f(x)=-x2+2x,则f(1)= .?
解析:∵当x<0时,f(x)=-x2+2x,
∴f(-1)=-(-1)2+2×(-1)=-3.
又f(x)为奇函数,∴f(1)=-f(-1)=3.
答案:31.利用函数单调性的性质判断函数的单调性
剖析若函数f(x),g(x)在区间D上具有单调性,则在区间D上具有以下性质:
(1)f(x)与-f(x)具有相反的单调性.
(2)f(x)与f(x)+c(c为常数)具有相同的单调性.
(3)当a>0时,f(x)与af(x)具有相同的单调性;当a<0时,f(x)与af(x)具有相反的单调性.(5)当f(x),g(x)都是增(减)函数时,f(x)+g(x)也是增(减)函数.2.函数奇偶性的判断方法
剖析:(1)定义法
根据函数奇偶性的定义进行判断,步骤如下:
①判断函数f(x)的定义域是否关于原点对称.
若不对称,则函数f(x)为非奇非偶函数;若对称,则进行下一步.
②验证.f(-x)=-f(x)或f(-x)=f(x).
③下结论.
若f(-x)=-f(x),则f(x)为奇函数;
若f(-x)=f(x),则f(x)为偶函数;
若f(-x)≠-f(x),且f(-x)≠f(x),则f(x)为非奇非偶函数;若f(-x)=-f(x),且 f(-x)=f(x),则f(x)既是奇函数也是偶函数.(2)图象法
f(x)是奇(偶)函数的条件是f(x)的图象关于原点(y轴)对称.
(3)性质法
①偶函数的和、差、积、商(分母不为零)仍为偶函数;
②奇函数的和、差仍为奇函数;
③奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;
④一个奇函数与一个偶函数的积为奇函数.题型一题型二题型三题型四求函数的定义域和函数值故x=-1或x=3.
答案:(1){x|x≤4,且x≠-1} (2)-1或3题型一题型二题型三题型四反思1.求函数的定义域就是求使函数解析式有意义的自变量的取值集合.如果函数的解析式是由几部分组成,那么它的定义域就是使各部分有意义的自变量的取值集合的交集.
定义域的表示方法与集合的表示方法相同.
2.对于分段函数的函数值,应采用分类讨论思想即分段进行求解.各段独立进行,分别讨论求解.题型一题型二题型三题型四解析:(1)根据题意知g(x)的定义域为B={x|x
(2)f(7)=f(f(11))=f(8)=f(f(12))=f(9)=6.
答案:(1)a≤3 (2)6题型一题型二题型三题型四求函数的值域
【例2】 (1)函数f(x)=-x2+4x,x∈[0,3)的值域为 ;?解析:(1)(方法1)函数f(x)=-x2+4x为二次函数,图象开口向下,且对称轴为x=2.故当x∈[0,2]时,f(x)单调递增;当x∈(2,3)时,f(x)单调递减.∴当x∈[0,3)时,f(x)max=f(2)=4,f(x)min=f(0)=0.∴f(x)的值域为[0,4].
(方法2)画出函数f(x)=-x2+4x,x∈[0,3)的图象,如图所示,观察图象可得f(x)的值域为[0,4].∴y≠2,故函数值域为{y|y∈R,且y≠2}.
答案:(1)[0,4] (2){y|y∈R,且y≠2}题型一题型二题型三题型四反思求函数值域的方法:
(1)观察法;(2)图象法;(3)单调性法;(4)分离常数法.题型一题型二题型三题型四题型一题型二题型三题型四函数单调性与奇偶性的综合运用
【例3】 (1)已知定义在R上的偶函数f(x)满足:对任意的x1,x2∈ (-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
A.f(-n)
得f(x)在区间(-∞,0]上为增函数.
∵f(x)为偶函数,
∴f(x)在区间[0,+∞)内为减函数.
又f(-n)=f(n),且0≤n-1
得f(1-a2)<-f(1-a).
∵y=f(x)在区间[-1,1]上是奇函数,
∴-f(1-a)=f(a-1),
∴f(1-a2)
1.比较大小问题,一般解法是先利用奇偶性,将不在同一单调区间上的两个或多个自变量的函数值,转化为其对称区间上的函数值,使其在同一单调区间上,然后利用单调性比较大小.
2.抽象不等式问题,解题步骤是:(1)将所给的不等式转化为两个函数值的大小关系;(2)利用奇偶性得出区间上的单调性,再利用单调性“脱去”函数的符号“f”,转化为解不等式(组)的问题.
需要注意的是:在转化时,自变量的取值必须在同一单调区间上;当不等式一边没有符号“f”时,需转化为含符号“f”的形式,如0=f(1),f(x-1)<0,则f(x-1)
C.f(3)>f(-2)>f(-π) D.f(3)>f(-π)>f(-2)
(2)已知偶函数f(x)在区间[0,+∞)内单调递增,则满足f(2x-1)<题型一题型二题型三题型四解析:(1)∵f(x)是R上的偶函数,
∴f(-2)=f(2),f(-π)=f(π),
又f(x)在区间[0,+∞)上单调递增,且2<3<π,
∴f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2).
(2)由于f(x)为偶函数,且在[0,+∞)上单调递增,答案:(1)A (2)A 题型一题型二题型三题型四抽象函数的单调性与奇偶性问题
【例4】 设函数f(x)对任意x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数.
(2)试问:当-3≤x≤3时,f(x)是否有最值?如果有,求出最值;如果没有,请说明理由.
分析:(1)f(x+y)=f(x)+f(y)对一切x,y∈R均成立,
先计算f(0),再令y=-x,可证得f(x)为奇函数.
(2)利用函数的单调性来确定是否存在最值.题型一题型二题型三题型四解:(1)令x=y=0,
则有f(0+0)=f(0)+f(0),
即f(0)=2f(0),解得f(0)=0.令y=-x,
则有0=f(0)=f(x)+f(-x),故f(x)为奇函数.
(2)任取x1,x2,且-3≤x1
由题意得f(x2-x1)<0,且
f(x1)-f(x2)=f(x1)-f[x1+(x2-x1)]=f(x1)-[f(x1)+f(x2-x1)]=-f(x2-x1)>0,
即f(x1)>f(x2),∴f(x)在区间[-3,3]上为减函数.
∴f(3)为函数的最小值,f(-3)为函数的最大值.
f(3)=f(1+1+1)=3f(1)=-6,
f(-3)=-f(3)=6,
∴当-3≤x≤3时,函数f(x)的最大值、最小值分别为6,-6.题型一题型二题型三题型四反思抽象函数奇偶性和单调性的判断方法
1.判断或证明抽象函数的奇偶性,需利用奇函数、偶函数的定义,找准方向,巧妙赋值,合理、灵活地变形配凑,找出f(x)与f(-x)的关系.
2.判断或证明抽象函数的单调性,通常有两种方法.
一种是“凑”,凑定义或凑已知,从而使用定义或已知条件得出结论;另一种是“赋值”,给变量赋值要根据条件与结论的关系,有时可能要进行多次尝试.
注意:若给出的是和型(f(x+y)=…)抽象函数,则判定符号时的变形为f(x2)-f(x1)=f((x2-x1)+x1)-f(x1),f(x2)-f(x1)=f(x2)-f((x1-x2)+x2);
若给出的是积型(f(xy)=…)抽象函数,则判定符号时的变形为题型一题型二题型三题型四【变式训练4】 已知函数f(x)的定义域是(0,+∞),当x>1时,f(x)>0,且f(x·y)=f(x)+f(y).
(1)求f(1);
(2)证明:f(x)在定义域上是增函数.
(1)解:令x=y=1,得f(1)=2f(1),故f(1)=0.故f(x)在区间(0,+∞)内是增函数.
