高中数学必修1人教版:2.1指数与指数函数教案
文档属性
| 名称 | 高中数学必修1人教版:2.1指数与指数函数教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 43.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-06 00:00:00 | ||
图片预览


文档简介
指数与指数函数
课题名称
指数与指数函数
教师姓名
文健
学生年级
高一
课时
1
课程标准描述
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
考试大纲描述
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
教材内容分析
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
学生分析
学习目标
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
重点
掌握指数函数图象、性质,能应用性质解决简单问题
难点[]
与指数函数相关的复合函数问题的处理
教学过程
教师活动
学生活动
设计意图(备注)
导
1.分数指数幂
(1)规定:正数的正分数指数幂的意义是a= (a>0,m,n∈N*,且n>1);正数的负分数指数幂的意义是a= (a>0,m,n∈N*,且n>1);0的正分数指数幂等于0;0的负分数指数幂没有意义.
(2)有理数指数幂的运算性质:=,,,其中a>0,b>0,r,s∈Q.
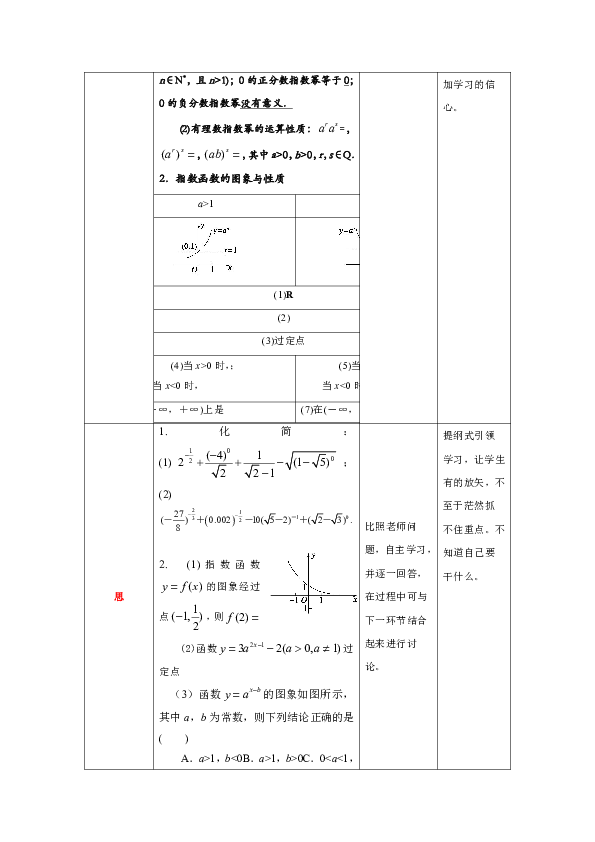
2.指数函数的图象与性质
y=ax
a>1
0图象
定义域
(1)R
值域
(2)
性质
(3)过定点
(4)当x>0时,;
当x<0时,
(5)当x>0时,;
当x<0时,
(6)在(-∞,+∞)上是
(7)在(-∞,+∞)上是
口头回答
问题引如,激发学生兴趣,学生易于从书上内容中找到答案。增加学习的信心。
思
1.化简:(1);(2)
2. (1)指数函数的图象经过点,则
(2)函数过定点
(3)函数的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0B.a>1,b>0C.00D.03.(1)下列各式比较大小正确的是( )
A.1.72.5>1.73 B.0.6-1>0.62C.0.8-0.1>1.250.2 D.1.70.3<0.93.1
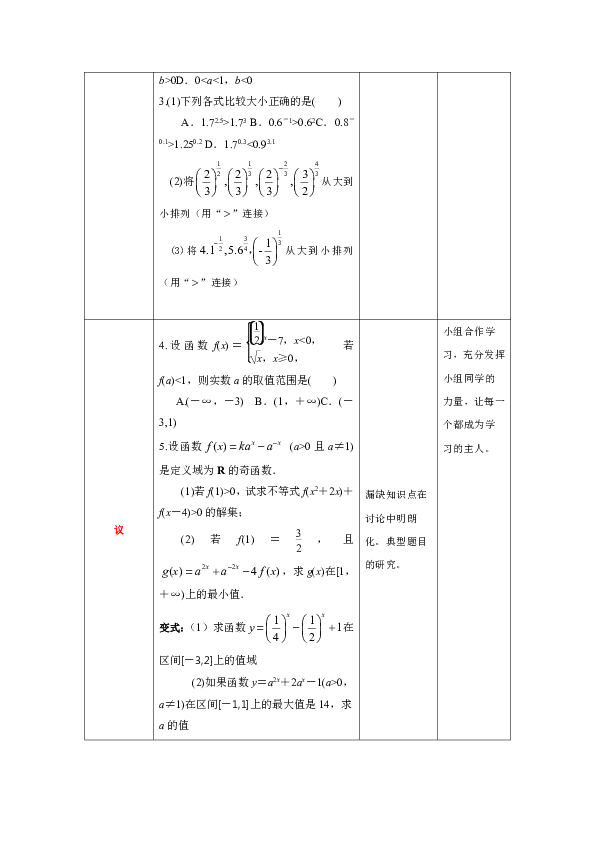
(2)将从大到小排列(用“”连接)
(3)将从大到小排列(用“”连接)
比照老师问题,自主学习,并逐一回答,在过程中可与下一环节结合起来进行讨论。
提纲式引领学习,让学生有的放矢,不至于茫然抓不住重点。不知道自己要干什么。
议
4.设函数f(x)=若f(a)<1,则实数a的取值范围是( )
A.(-∞,-3) B.(1,+∞)C.(-3,1) D.(-∞,-3)∪(1,+∞)
5.设函数 (a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(2)若f(1)=,且,求g(x)在[1,+∞)上的最小值.
变式:(1)求函数在区间[-3,2]上的值域
(2)如果函数y=a2x+2ax-1(a>0,a≠1)在区间[-1,1]上的最大值是14,求a的值
(3)求函数的单调减区间
漏缺知识点在讨论中明朗化。典型题目的研究。
小组合作学习,充分发挥小组同学的力量,让每一个都成为学习的主人。
展
收集每个小组中所存在的问题。对重难点知识的梳理。
由小组长带头总结
集体讨论,各个击破。
评
老师对议中的问题进行整理,并选择解决方式,可由其他小组学生带答(比较简单的)也可由老师做一阐述(较难,易混淆的)
各种题型的反思。
听同学或老师讲解。
知识形成体系,对于该节内容有了一个比较清晰的认识。
检
P27页练习题
学生完成
速度质量的考查
教学反思
教学后完成
检查结果及修改意见:
合格[ ] 不合格[ ]
教研组长(签字):
检查日期:年月日
课题名称
指数与指数函数
教师姓名
文健
学生年级
高一
课时
1
课程标准描述
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
考试大纲描述
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
教材内容分析
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
学生分析
学习目标
掌握指数运算相关规则,能熟练进行根式与指数互化.;
掌握指数函数图象、性质,能应用性质解决简单问题;
与指数函数相关的复合函数问题的处理
重点
掌握指数函数图象、性质,能应用性质解决简单问题
难点[]
与指数函数相关的复合函数问题的处理
教学过程
教师活动
学生活动
设计意图(备注)
导
1.分数指数幂
(1)规定:正数的正分数指数幂的意义是a= (a>0,m,n∈N*,且n>1);正数的负分数指数幂的意义是a= (a>0,m,n∈N*,且n>1);0的正分数指数幂等于0;0的负分数指数幂没有意义.
(2)有理数指数幂的运算性质:=,,,其中a>0,b>0,r,s∈Q.
2.指数函数的图象与性质
y=ax
a>1
0
定义域
(1)R
值域
(2)
性质
(3)过定点
(4)当x>0时,;
当x<0时,
(5)当x>0时,;
当x<0时,
(6)在(-∞,+∞)上是
(7)在(-∞,+∞)上是
口头回答
问题引如,激发学生兴趣,学生易于从书上内容中找到答案。增加学习的信心。
思
1.化简:(1);(2)
2. (1)指数函数的图象经过点,则
(2)函数过定点
(3)函数的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0B.a>1,b>0C.0
A.1.72.5>1.73 B.0.6-1>0.62C.0.8-0.1>1.250.2 D.1.70.3<0.93.1
(2)将从大到小排列(用“”连接)
(3)将从大到小排列(用“”连接)
比照老师问题,自主学习,并逐一回答,在过程中可与下一环节结合起来进行讨论。
提纲式引领学习,让学生有的放矢,不至于茫然抓不住重点。不知道自己要干什么。
议
4.设函数f(x)=若f(a)<1,则实数a的取值范围是( )
A.(-∞,-3) B.(1,+∞)C.(-3,1) D.(-∞,-3)∪(1,+∞)
5.设函数 (a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(2)若f(1)=,且,求g(x)在[1,+∞)上的最小值.
变式:(1)求函数在区间[-3,2]上的值域
(2)如果函数y=a2x+2ax-1(a>0,a≠1)在区间[-1,1]上的最大值是14,求a的值
(3)求函数的单调减区间
漏缺知识点在讨论中明朗化。典型题目的研究。
小组合作学习,充分发挥小组同学的力量,让每一个都成为学习的主人。
展
收集每个小组中所存在的问题。对重难点知识的梳理。
由小组长带头总结
集体讨论,各个击破。
评
老师对议中的问题进行整理,并选择解决方式,可由其他小组学生带答(比较简单的)也可由老师做一阐述(较难,易混淆的)
各种题型的反思。
听同学或老师讲解。
知识形成体系,对于该节内容有了一个比较清晰的认识。
检
P27页练习题
学生完成
速度质量的考查
教学反思
教学后完成
检查结果及修改意见:
合格[ ] 不合格[ ]
教研组长(签字):
检查日期:年月日
