高中物理教科版选修3-1 能力提升训练第三章 磁场检测(B) Word版含解析
文档属性
| 名称 | 高中物理教科版选修3-1 能力提升训练第三章 磁场检测(B) Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 552.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-09-05 00:00:00 | ||
图片预览




文档简介
第三章检测(B)
(时间90分钟,满分100分)
一、选择题(本题包含10小题,每小题4分,共40分.在每小题给出的四个选项中,1~6题只有一个选项符合题目要求,7~10题有多个选项符合题目要求,全部选对的得4分,选对但不全的得2分,有选错的得0分)
/1.下列说法正确的是( )
A.磁感应强度是矢量,它的方向与通电导线在磁场中所受磁场力的方向相同
B.磁感应强度的单位是特斯拉,1 T=1 N/(A·m2)
C.磁通量的大小等于穿过线圈单位面积的磁感线条数
D.磁通量的单位是韦伯,1 Wb=1 T·m2
解析:磁感应强度的方向与通电导线在磁场中所受磁场力的方向是垂直的,故选项A错误.由F=BIL得B=
??
????
,单位关系1 T=1 N/(A·m),故选项B错误.磁通量的大小等于穿过某一面积的磁感线条数,选项C错误.由Φ=BS知单位关系1 Wb=1 T·m2是正确的,选项D正确.
答案:D
/2.如图所示,真空中两点电荷+q和-q以共同的角速度绕轴OO'匀速运动,P点距+q近,则P点磁感应强度的方向为( )
/
A.沿O'O向上 B.沿OO'向下
C.从+q指向-q D.磁感应强度为0
解析:电荷的定向移动形成电流,当两个点电荷匀速转动时,相当于产生两个环形电流,由I=
??
??
知两个电荷产生的等效电流大小相等,+q产生的电流形成的磁场在P点方向向上,-q产生的电流形成的磁场在P点方向向下,但由于P点离+q近,+q形成的电流在P点产生的磁感应强度大,因此P点磁感应强度方向应沿O'O向上,故选项A正确.
答案:A
/3.如图所示,正六边形abcdef区域内有垂直于纸面的匀强磁场.一带正电的粒子从f点沿fd方向射入磁场区域,当速度大小为vb时,从b点离开磁场,在磁场中运动的时间为tb;当速度大小为vc时,从c点离开磁场,在磁场中运动的时间为tc,不计粒子重力.则( )
/
A.vb∶vc=1∶2,tb∶tc=2∶1
B.vb∶vc=2∶1,tb∶tc=1∶2
C.vb∶vc=2∶1,tb∶tc=2∶1
D.vb∶vc=1∶2,tb∶tc=1∶2
解析:设正六边形边长为l.对于粒子从f点沿fd方向射入磁场区域,从b点离开磁场的过程,粒子做匀速圆周运动的圆心为a点,则速度偏转角即圆弧所对圆心角为θb=120°,半径rb=l;对于粒子速度大小为vc从c点离开磁场的过程,圆弧对应弦切角为60°,则速度偏转角即圆弧所对圆心角为θc=60°,半径rc=2l;由牛顿第二定律,qvB=
??
??
2
??
,得v=
??????
??
,由于rb∶rc=1∶2,所以vb∶vc=1∶2.由T=
2π??
????
,得??=
2π
??
=
????
??
,可知两种情况中粒子角速度相等.由t=
??
??
,且θb∶θc=2∶1,所以tb∶tc=2∶1,故选A.
/
答案:A
/4.已知通电长直导线产生的磁场中某点的磁感应强度满足B=??
??
??
(其中??为比例系数,??为电流,
??为该点到直导线的距离).现有四根平行的通电长直导线,其横截面积恰好在一个边长为??的正方形的四个顶点上,电流方向如图所示,其中??、??导线中的电流大小为??1,??、??导线中的电流大小为??2.已知??导线所受的磁场力恰好为零,则下列说法不正确的是( )
/
A.电流的大小关系为I1=2I2
B.四根导线所受的磁场力为零
C.正方形中心O处的磁感应强度为零
D.若移走A导线,则中心O处的磁场将沿OB方向
解析:导线B、C、D在导线A处的磁场如图甲所示,根据题意A导线的磁场力为零,则A处的合磁场为零,即
2
??
??
2
??
=??
??
1
2
??
,则I1=2I2,故选项A正确;同理将各点的磁场都画出,可以判断B、D导线处的合磁场不为零,故磁场力不为零,故选项B错误;将各导线在O点的磁场画出,如图乙所示,由于A、C导线电流相等而且距离O点距离相等,则BA'=BC',同理BB'=BD',即正方形中心O处的磁感应强度为零,故选项C正确;若移走A导线,则磁场BA'不存在,由于BB'=BD',则此时在O点的磁场只剩下导线C的磁场,而且导线C点磁场方向沿OB方向,即中心O处的磁场将沿OB方向,故选项D正确.
/
甲
/
乙
答案:B
/5.如图所示,在匀强电场和匀强磁场共存的区域内,电场的电场强度为E,方向竖直向下,磁场的磁感应强度为B,方向垂直于纸面向里,一质量为m的带电质点,在场区内的一竖直平面内做匀速圆周运动,则可判断该带电质点( )
/
A.带有电荷量为
????
??
的正电荷
B.沿圆周逆时针运动
C.运动的角速度为
????
??
D.运动的速率为
??
??
解析:带电质点在竖直平面内做匀速圆周运动,有mg=qE,求得电荷量q=
????
??
,根据电场强度方向和电场力方向判断出质点带负电,选项A错误.由左手定则可判断质点沿顺时针方向运动,选项B错误.由qvB=mvω得ω=
????
??
=
??????
????
=
????
??
,选项C正确.在速度选择器中才有v=
??
??
,故选项D错误.
答案:C
/6.如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷.一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
/
A.若微粒带正电荷,则A板一定带正电荷
B.微粒从M点运动到N点电势能一定增加
C.微粒从M点运动到N点动能一定增加
D.微粒从M点运动到N点机械能一定增加
解析:由于不知道重力和电场力大小关系,所以不能确定电场力方向,不能确定微粒电性,也不能确定电场力对微粒做功的正负,则选项A、B、D错误;根据微粒偏转方向可知微粒所受合外力一定是竖直向下,则合外力对微粒做正功,由动能定理知微粒的动能一定增加,选项C正确.
答案:C
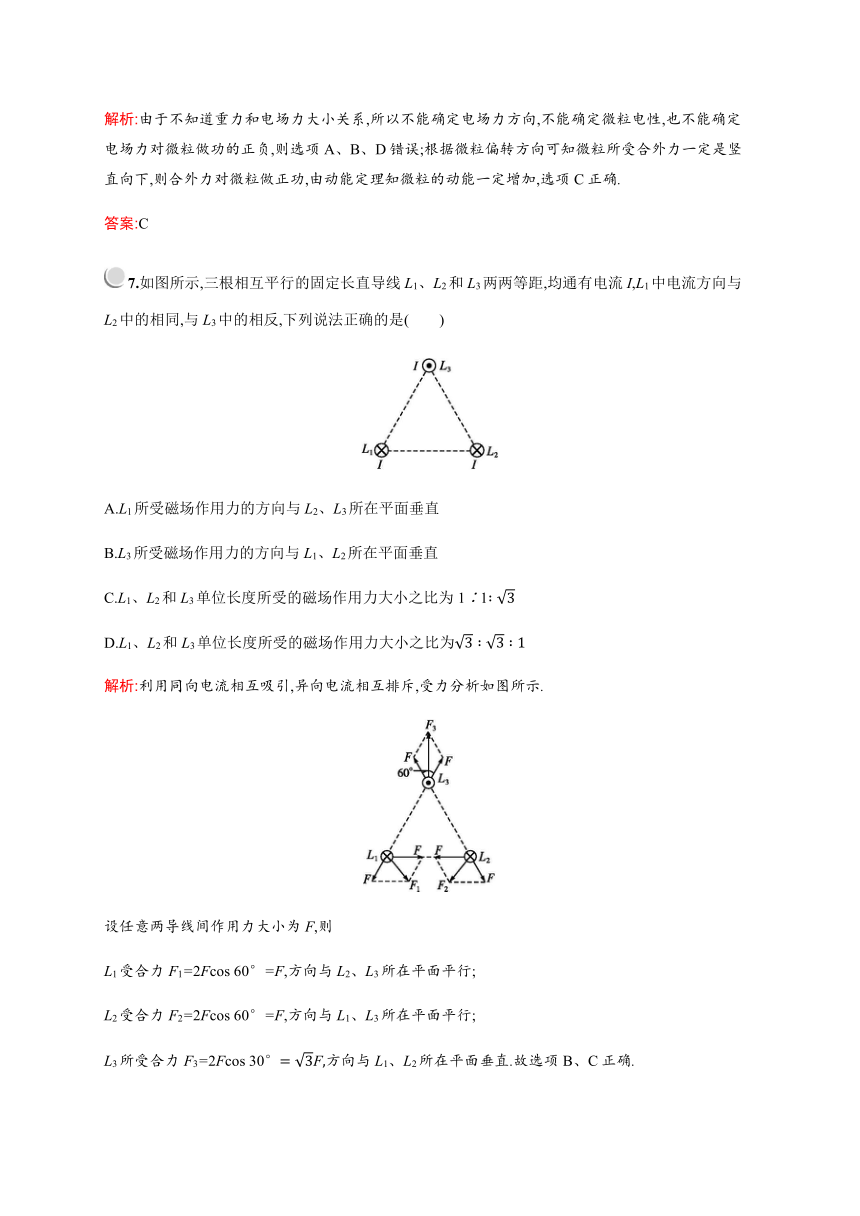
/7.如图所示,三根相互平行的固定长直导线L1、L2和L3两两等距,均通有电流I,L1中电流方向与L2中的相同,与L3中的相反,下列说法正确的是( )
/
A.L1所受磁场作用力的方向与L2、L3所在平面垂直
B.L3所受磁场作用力的方向与L1、L2所在平面垂直
C.L1、L2和L3单位长度所受的磁场作用力大小之比为1∶1∶
3
D.L1、L2和L3单位长度所受的磁场作用力大小之比为
3
∶
3
∶1
解析:利用同向电流相互吸引,异向电流相互排斥,受力分析如图所示.
/
设任意两导线间作用力大小为F,则
L1受合力F1=2Fcos 60°=F,方向与L2、L3所在平面平行;
L2受合力F2=2Fcos 60°=F,方向与L1、L3所在平面平行;
L3所受合力F3=2Fcos 30°=
3
??,方向与L1、L2所在平面垂直.故选项B、C正确.
答案:BC
/8.如图所示,连接平行金属板P1和P2(板面垂直于纸面)的导线的一部分CD和另一连接电池的回路的一部分GH平行,CD和GH均在纸平面内,金属板置于磁场中,磁场方向垂直于纸面向里,当一束等离子体射入两金属板之间时,CD段导线将受到力的作用,下列判断正确的是( )
/
A.当等离子体从右侧射入时,CD受力的方向背离GH
B.当等离子体从右侧射入时,CD受力的方向指向GH
C.当等离子体从左侧射入时,CD受力的方向背离GH
D.当等离子体从左侧射入时,CD受力的方向指向GH
解析:由电路知识知GH中的电流方向向下.等离子体从右方射入时,由左手定则可知,正离子向下偏转,负离子向上偏转,CD中的电流方向向上,由异向平行的电流相互排斥可知,CD受力的方向背离GH,选项A正确,选项B错误.同理可知,等离子体从左方射入时,CD受力的方向指向GH,选项C错误,选项D正确.
答案:AD
/9.如图所示,一束带电粒子以一定的初速度沿直线通过由相互正交的匀强磁场B和匀强电场E组成的速度选择器,然后粒子通过平板S上的狭缝P,进入另一匀强磁场B',最终打在A1A2上.下列表述正确的是( )
/
A.粒子带负电
B.所有打在A1A2上的粒子,在磁场B'中运动时间都相同
C.能通过狭缝P的带电粒子的速率等于
??
??
D.粒子打在A1A2上的位置越靠近P,粒子的比荷
??
??
越大
解析:根据题图粒子轨迹,利用左手定则可知粒子带正电,选项A错误;根据带电粒子在匀强磁场中运动洛伦兹力等于向心力,其运动周期T=
2π??
????
,所有打在A1A2上的粒子,在磁场B'中运动时间都为半个周期,时间与粒子比荷成反比,选项B错误;带电粒子以一定的初速度沿直线通过由相互正交的匀强磁场B和匀强电场E组成的速度选择器,满足qE=qvB,能通过狭缝P的带电粒子的速率等于v=
??
??
,选项C正确;根据带电粒子在匀强磁场中运动洛伦兹力等于向心力,其轨迹半径r=
????
????
,粒子打在A1A2上的位置越靠近P,轨迹半径r越小,粒子的比荷
??
??
越大,选项D正确.
答案:CD
/10.如图所示,MN是磁感应强度为B的匀强磁场的边界.一质量为m、电荷量为q的粒子(重力不计)在纸面内从O点射入磁场.若粒子速度为v0,最远能落在边界上的A点.下列说法正确的有( )
/
A.若粒子落在A点的左侧,其速度一定小于v0
B.若粒子落在A点的右侧,其速度一定大于v0
C.若粒子落在A点左右两侧d的范围内,其速度不可能小于v0?
??????
2??
D.若粒子落在A点左右两侧d的范围内,其速度不可能大于v0+
??????
2??
解析:由牛顿第二定律可得qv0B=??
??
0
2
??
,解得r=
??
??
0
????
,当粒子从O点垂直MN界面射入磁场时,粒子射出磁场位置与MN交点距入射点O最远,即OA=2r,当粒子以速度v0从O点沿任意方向入射时,一定打在OA内,选项A错误;结合前面分析只有v>v0时粒子才有可能打在A点的右侧,选项B正确;若r1=
1
2
(???????),则根据qvB=??
??
2
??
1
可得v=
????(????-??)
2??
,由上面可得v0=
????·????
2??
,则有v=v0?
??????
2??
,只有v≥v0?
??????
2??
时,粒子才可能落入该范围内,选项C正确;若粒子以v2垂直MN边界射入磁场恰好到达距A点右侧d位置时,r2=
1
2
(????+??),同理可推得v2=v0+
??????
2??
,当粒子速度v>v2时,只要粒子不垂直MN射入磁场,也有可能落到距A点右侧d位置以内,选项D错误.
答案:BC
二、填空题(本题包含2小题,共14分)
/11.(4分)如图所示,正方形线框abcd边长为L,悬挂在等臂天平的一侧,线框的下端处在一个如图所示的匀强磁场中,调节天平右盘的砝码使天平平衡,如果线框中通过电流为I,则需要在右盘中加一个质量为Δm的砝码,天平再次平衡.线框bc段上的电流方向是 ,磁场的磁感应强度大小是 .?
/
答案:c→b
Δ????
????
/12.(10分)如图所示,厚度为h、宽度为d的导体板放在垂直于它的磁感应强度为B的均匀磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A'之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=
??·????
??
,式中的比例系数??称为霍尔系数.霍尔效应可解释如下:外部磁场的洛伦兹力使运动的电子聚集在导体板的一侧,在导体板的另一侧出现多余的正电荷,从而形成横向电场;横向电场对电子施加与洛伦兹力方向相反的静电力,当静电力与洛伦兹力达到平衡时,导体板上下两侧之间就会形成稳定的电势差.设电流??是电子的定向流动形成的,电子的平均定向速度为??,电荷量为??,回答下列问题:
/
(1)达到稳定状态时,导体板上侧面A的电势 (选填“高于”“低于”或“等于”)下侧面A'的电势;?
(2)电子所受洛伦兹力的大小为 ;?
(3)当导体板上下两侧面之间的电势差为U时,电子所受静电力的大小为 ;?
(4)由静电力和洛伦兹力平衡的条件,证明霍尔系数为K=
1
????
,其中??代表导体板单位体积中电子的个数.
解析:(1)由左手定则可知电子所受洛伦兹力方向向上,根据题意知静电力方向向下,电场强度方向向上,所以φA<φA'.
(2)由洛伦兹力公式得F洛=Bev.
(3)F=qE=
????
?
或F=F洛=Bev.
(4)电子受到横向的静电力F与洛伦兹力F洛相平衡,即
????
?
=??????.0①
通过导体板的电流
I=
??
??
=
??(??·??Δ??)??
Δ??
=????????=?????????.0②
已知公式U=
??·????
??
,0③
由①②③式得K=
1
????
.
答案:(1)低于 (2)Bev (3)
????
?
(或??????) (4)见解析
三、计算题(本题包含4小题,共46分)
/13.(10分)如图所示,在倾角为θ=30°的斜面上,固定一宽L=0.25 m 的平行金属导轨,在导轨上端接入电源和滑动变阻器.电源电动势E=12 V,内阻为r=1.0 Ω.一质量 m=20 g的金属棒ab与两导轨垂直并接触良好.整个装置处于磁感应强度B=0.80 T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计).金属导轨是光滑的,g取10 m/s2,要保持金属棒在导轨上静止,求:
/
(1)金属棒所受到的安培力;
(2)通过金属棒的电流;
(3)滑动变阻器R接入到电路中的阻值.
解析:(1)F=mgsin 30°
F=0.1 N.
(2)金属棒静止在金属轨道上受力平衡,
/
如图所示
解得I=
??
????
=0.5 A.
(3)设变阻器接入电路的阻值为R,根据闭合电路欧姆定律E=I(R+r)
解得R=
??
??
???=23 Ω.
答案:(1)0.1 N (2)0.5 A (3)23 Ω
/14.(10分)如图所示,在半径R的圆形区域内,分布着磁感应强度大小为B的匀强磁场.在圆心处发射一个运动方向与磁场垂直的电子,电子质量为m,电荷量为e.求这个电子要穿离此磁场区域应具有的最小动能.
/
解析:电子刚好不穿离磁场区域的条件是其轨迹正好和圆相切,故电子运动的半径r=
1
2
??.0①
电子做圆周运动的向心力由洛伦兹力提供,即evB=
??
??
2
??
0②
而动能Ek=
1
2
??
??
2
0③
三式联立可得Ek=
??
2
??
2
??
2
8??
.
答案:
??
2
??
2
??
2
8??
/15.(12分)如图所示,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m、电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.
/
(1)求小滑块运动到C点时的速度大小vC;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点.已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vP.
解析:(1)小滑块沿MN运动过程,水平方向受力满足
qvB+N=qE
小滑块在C点离开MN时N=0
解得vC=
??
??
.
(2)由动能定理mgh-Wf=
1
2
??
??
??
2
?0
解得Wf=mgh?
??
??
2
2
??
2
.
/
(3)如图,小滑块速度最大时,速度方向与电场力、重力的合力方向垂直.撤去磁场后小滑块将做类平抛运动,等效加速度为g'
g'=
????
??
2
+
??
2
且
??
??
2
=
??
??
2
+
??′
2
??
2
解得
vP=
??
??
2
+
????
??
2
+
??
2
??
2
.
答案:(1)
??
??
(2)??????
??
??
2
2
??
2
(3)
??
??
2
+
????
??
2
+
??
2
??
2
/16.(14分)(2018·全国Ⅱ卷)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示:中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l',电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行,一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出.不计重力.
/
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为
π
6
,求该粒子的比荷及其从??点运动到??点的时间.
解析:(1)粒子运动的轨迹如图甲所示.(粒子在电场中的轨迹为抛物线,在磁场中为圆弧,上下对称)
/
甲
/
乙
(2)粒子从电场下边界入射后在电场中做类平抛运动.设粒子从M点射入时速度的大小为v0,在下侧电场中运动的时间为t,加速度的大小为a;粒子进入磁场的速度大小为v,方向与电场方向的夹角为θ(见图乙),速度沿电场方向的分量为v1,根据牛顿第二定律有
qE=ma①
式中q和m分别为粒子的电荷量和质量.由运动学公式有
v1=at②
l'=v0t③
v1=vcos θ④
粒子在磁场中做匀速圆周运动,设其运动轨道半径为R,由洛伦兹力公式和牛顿第二定律得
qvB=
??
??
2
??
0⑤
由几何关系得l=2Rcos θ⑥
联立①②③④⑤⑥式得v0=
2????'
????
.0⑦
(3)由运动学公式和题给数据得
v1=v0cot
π
6
⑧
联立①②③⑦⑧式得
??
??
=
4
3
????'
??
2
??
2
0⑨
设粒子由M点运动到N点所用的时间为t',则
t'=2t+
2
π
2
-
π
6
2π
??0⑩
式中T是粒子在磁场中做匀速圆周运动的周期,
T=
2π??
????
/
由③⑦⑨⑩/式得
t'=
????
??
1+
3
π??
18??'
.0/
答案:(1)见解析图 (2)
2????'
????
(3)
4
3
????'
??
2
??
2
????
??
1+
3
π??
18??'
(时间90分钟,满分100分)
一、选择题(本题包含10小题,每小题4分,共40分.在每小题给出的四个选项中,1~6题只有一个选项符合题目要求,7~10题有多个选项符合题目要求,全部选对的得4分,选对但不全的得2分,有选错的得0分)
/1.下列说法正确的是( )
A.磁感应强度是矢量,它的方向与通电导线在磁场中所受磁场力的方向相同
B.磁感应强度的单位是特斯拉,1 T=1 N/(A·m2)
C.磁通量的大小等于穿过线圈单位面积的磁感线条数
D.磁通量的单位是韦伯,1 Wb=1 T·m2
解析:磁感应强度的方向与通电导线在磁场中所受磁场力的方向是垂直的,故选项A错误.由F=BIL得B=
??
????
,单位关系1 T=1 N/(A·m),故选项B错误.磁通量的大小等于穿过某一面积的磁感线条数,选项C错误.由Φ=BS知单位关系1 Wb=1 T·m2是正确的,选项D正确.
答案:D
/2.如图所示,真空中两点电荷+q和-q以共同的角速度绕轴OO'匀速运动,P点距+q近,则P点磁感应强度的方向为( )
/
A.沿O'O向上 B.沿OO'向下
C.从+q指向-q D.磁感应强度为0
解析:电荷的定向移动形成电流,当两个点电荷匀速转动时,相当于产生两个环形电流,由I=
??
??
知两个电荷产生的等效电流大小相等,+q产生的电流形成的磁场在P点方向向上,-q产生的电流形成的磁场在P点方向向下,但由于P点离+q近,+q形成的电流在P点产生的磁感应强度大,因此P点磁感应强度方向应沿O'O向上,故选项A正确.
答案:A
/3.如图所示,正六边形abcdef区域内有垂直于纸面的匀强磁场.一带正电的粒子从f点沿fd方向射入磁场区域,当速度大小为vb时,从b点离开磁场,在磁场中运动的时间为tb;当速度大小为vc时,从c点离开磁场,在磁场中运动的时间为tc,不计粒子重力.则( )
/
A.vb∶vc=1∶2,tb∶tc=2∶1
B.vb∶vc=2∶1,tb∶tc=1∶2
C.vb∶vc=2∶1,tb∶tc=2∶1
D.vb∶vc=1∶2,tb∶tc=1∶2
解析:设正六边形边长为l.对于粒子从f点沿fd方向射入磁场区域,从b点离开磁场的过程,粒子做匀速圆周运动的圆心为a点,则速度偏转角即圆弧所对圆心角为θb=120°,半径rb=l;对于粒子速度大小为vc从c点离开磁场的过程,圆弧对应弦切角为60°,则速度偏转角即圆弧所对圆心角为θc=60°,半径rc=2l;由牛顿第二定律,qvB=
??
??
2
??
,得v=
??????
??
,由于rb∶rc=1∶2,所以vb∶vc=1∶2.由T=
2π??
????
,得??=
2π
??
=
????
??
,可知两种情况中粒子角速度相等.由t=
??
??
,且θb∶θc=2∶1,所以tb∶tc=2∶1,故选A.
/
答案:A
/4.已知通电长直导线产生的磁场中某点的磁感应强度满足B=??
??
??
(其中??为比例系数,??为电流,
??为该点到直导线的距离).现有四根平行的通电长直导线,其横截面积恰好在一个边长为??的正方形的四个顶点上,电流方向如图所示,其中??、??导线中的电流大小为??1,??、??导线中的电流大小为??2.已知??导线所受的磁场力恰好为零,则下列说法不正确的是( )
/
A.电流的大小关系为I1=2I2
B.四根导线所受的磁场力为零
C.正方形中心O处的磁感应强度为零
D.若移走A导线,则中心O处的磁场将沿OB方向
解析:导线B、C、D在导线A处的磁场如图甲所示,根据题意A导线的磁场力为零,则A处的合磁场为零,即
2
??
??
2
??
=??
??
1
2
??
,则I1=2I2,故选项A正确;同理将各点的磁场都画出,可以判断B、D导线处的合磁场不为零,故磁场力不为零,故选项B错误;将各导线在O点的磁场画出,如图乙所示,由于A、C导线电流相等而且距离O点距离相等,则BA'=BC',同理BB'=BD',即正方形中心O处的磁感应强度为零,故选项C正确;若移走A导线,则磁场BA'不存在,由于BB'=BD',则此时在O点的磁场只剩下导线C的磁场,而且导线C点磁场方向沿OB方向,即中心O处的磁场将沿OB方向,故选项D正确.
/
甲
/
乙
答案:B
/5.如图所示,在匀强电场和匀强磁场共存的区域内,电场的电场强度为E,方向竖直向下,磁场的磁感应强度为B,方向垂直于纸面向里,一质量为m的带电质点,在场区内的一竖直平面内做匀速圆周运动,则可判断该带电质点( )
/
A.带有电荷量为
????
??
的正电荷
B.沿圆周逆时针运动
C.运动的角速度为
????
??
D.运动的速率为
??
??
解析:带电质点在竖直平面内做匀速圆周运动,有mg=qE,求得电荷量q=
????
??
,根据电场强度方向和电场力方向判断出质点带负电,选项A错误.由左手定则可判断质点沿顺时针方向运动,选项B错误.由qvB=mvω得ω=
????
??
=
??????
????
=
????
??
,选项C正确.在速度选择器中才有v=
??
??
,故选项D错误.
答案:C
/6.如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷.一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
/
A.若微粒带正电荷,则A板一定带正电荷
B.微粒从M点运动到N点电势能一定增加
C.微粒从M点运动到N点动能一定增加
D.微粒从M点运动到N点机械能一定增加
解析:由于不知道重力和电场力大小关系,所以不能确定电场力方向,不能确定微粒电性,也不能确定电场力对微粒做功的正负,则选项A、B、D错误;根据微粒偏转方向可知微粒所受合外力一定是竖直向下,则合外力对微粒做正功,由动能定理知微粒的动能一定增加,选项C正确.
答案:C
/7.如图所示,三根相互平行的固定长直导线L1、L2和L3两两等距,均通有电流I,L1中电流方向与L2中的相同,与L3中的相反,下列说法正确的是( )
/
A.L1所受磁场作用力的方向与L2、L3所在平面垂直
B.L3所受磁场作用力的方向与L1、L2所在平面垂直
C.L1、L2和L3单位长度所受的磁场作用力大小之比为1∶1∶
3
D.L1、L2和L3单位长度所受的磁场作用力大小之比为
3
∶
3
∶1
解析:利用同向电流相互吸引,异向电流相互排斥,受力分析如图所示.
/
设任意两导线间作用力大小为F,则
L1受合力F1=2Fcos 60°=F,方向与L2、L3所在平面平行;
L2受合力F2=2Fcos 60°=F,方向与L1、L3所在平面平行;
L3所受合力F3=2Fcos 30°=
3
??,方向与L1、L2所在平面垂直.故选项B、C正确.
答案:BC
/8.如图所示,连接平行金属板P1和P2(板面垂直于纸面)的导线的一部分CD和另一连接电池的回路的一部分GH平行,CD和GH均在纸平面内,金属板置于磁场中,磁场方向垂直于纸面向里,当一束等离子体射入两金属板之间时,CD段导线将受到力的作用,下列判断正确的是( )
/
A.当等离子体从右侧射入时,CD受力的方向背离GH
B.当等离子体从右侧射入时,CD受力的方向指向GH
C.当等离子体从左侧射入时,CD受力的方向背离GH
D.当等离子体从左侧射入时,CD受力的方向指向GH
解析:由电路知识知GH中的电流方向向下.等离子体从右方射入时,由左手定则可知,正离子向下偏转,负离子向上偏转,CD中的电流方向向上,由异向平行的电流相互排斥可知,CD受力的方向背离GH,选项A正确,选项B错误.同理可知,等离子体从左方射入时,CD受力的方向指向GH,选项C错误,选项D正确.
答案:AD
/9.如图所示,一束带电粒子以一定的初速度沿直线通过由相互正交的匀强磁场B和匀强电场E组成的速度选择器,然后粒子通过平板S上的狭缝P,进入另一匀强磁场B',最终打在A1A2上.下列表述正确的是( )
/
A.粒子带负电
B.所有打在A1A2上的粒子,在磁场B'中运动时间都相同
C.能通过狭缝P的带电粒子的速率等于
??
??
D.粒子打在A1A2上的位置越靠近P,粒子的比荷
??
??
越大
解析:根据题图粒子轨迹,利用左手定则可知粒子带正电,选项A错误;根据带电粒子在匀强磁场中运动洛伦兹力等于向心力,其运动周期T=
2π??
????
,所有打在A1A2上的粒子,在磁场B'中运动时间都为半个周期,时间与粒子比荷成反比,选项B错误;带电粒子以一定的初速度沿直线通过由相互正交的匀强磁场B和匀强电场E组成的速度选择器,满足qE=qvB,能通过狭缝P的带电粒子的速率等于v=
??
??
,选项C正确;根据带电粒子在匀强磁场中运动洛伦兹力等于向心力,其轨迹半径r=
????
????
,粒子打在A1A2上的位置越靠近P,轨迹半径r越小,粒子的比荷
??
??
越大,选项D正确.
答案:CD
/10.如图所示,MN是磁感应强度为B的匀强磁场的边界.一质量为m、电荷量为q的粒子(重力不计)在纸面内从O点射入磁场.若粒子速度为v0,最远能落在边界上的A点.下列说法正确的有( )
/
A.若粒子落在A点的左侧,其速度一定小于v0
B.若粒子落在A点的右侧,其速度一定大于v0
C.若粒子落在A点左右两侧d的范围内,其速度不可能小于v0?
??????
2??
D.若粒子落在A点左右两侧d的范围内,其速度不可能大于v0+
??????
2??
解析:由牛顿第二定律可得qv0B=??
??
0
2
??
,解得r=
??
??
0
????
,当粒子从O点垂直MN界面射入磁场时,粒子射出磁场位置与MN交点距入射点O最远,即OA=2r,当粒子以速度v0从O点沿任意方向入射时,一定打在OA内,选项A错误;结合前面分析只有v>v0时粒子才有可能打在A点的右侧,选项B正确;若r1=
1
2
(???????),则根据qvB=??
??
2
??
1
可得v=
????(????-??)
2??
,由上面可得v0=
????·????
2??
,则有v=v0?
??????
2??
,只有v≥v0?
??????
2??
时,粒子才可能落入该范围内,选项C正确;若粒子以v2垂直MN边界射入磁场恰好到达距A点右侧d位置时,r2=
1
2
(????+??),同理可推得v2=v0+
??????
2??
,当粒子速度v>v2时,只要粒子不垂直MN射入磁场,也有可能落到距A点右侧d位置以内,选项D错误.
答案:BC
二、填空题(本题包含2小题,共14分)
/11.(4分)如图所示,正方形线框abcd边长为L,悬挂在等臂天平的一侧,线框的下端处在一个如图所示的匀强磁场中,调节天平右盘的砝码使天平平衡,如果线框中通过电流为I,则需要在右盘中加一个质量为Δm的砝码,天平再次平衡.线框bc段上的电流方向是 ,磁场的磁感应强度大小是 .?
/
答案:c→b
Δ????
????
/12.(10分)如图所示,厚度为h、宽度为d的导体板放在垂直于它的磁感应强度为B的均匀磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A'之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=
??·????
??
,式中的比例系数??称为霍尔系数.霍尔效应可解释如下:外部磁场的洛伦兹力使运动的电子聚集在导体板的一侧,在导体板的另一侧出现多余的正电荷,从而形成横向电场;横向电场对电子施加与洛伦兹力方向相反的静电力,当静电力与洛伦兹力达到平衡时,导体板上下两侧之间就会形成稳定的电势差.设电流??是电子的定向流动形成的,电子的平均定向速度为??,电荷量为??,回答下列问题:
/
(1)达到稳定状态时,导体板上侧面A的电势 (选填“高于”“低于”或“等于”)下侧面A'的电势;?
(2)电子所受洛伦兹力的大小为 ;?
(3)当导体板上下两侧面之间的电势差为U时,电子所受静电力的大小为 ;?
(4)由静电力和洛伦兹力平衡的条件,证明霍尔系数为K=
1
????
,其中??代表导体板单位体积中电子的个数.
解析:(1)由左手定则可知电子所受洛伦兹力方向向上,根据题意知静电力方向向下,电场强度方向向上,所以φA<φA'.
(2)由洛伦兹力公式得F洛=Bev.
(3)F=qE=
????
?
或F=F洛=Bev.
(4)电子受到横向的静电力F与洛伦兹力F洛相平衡,即
????
?
=??????.0①
通过导体板的电流
I=
??
??
=
??(??·??Δ??)??
Δ??
=????????=?????????.0②
已知公式U=
??·????
??
,0③
由①②③式得K=
1
????
.
答案:(1)低于 (2)Bev (3)
????
?
(或??????) (4)见解析
三、计算题(本题包含4小题,共46分)
/13.(10分)如图所示,在倾角为θ=30°的斜面上,固定一宽L=0.25 m 的平行金属导轨,在导轨上端接入电源和滑动变阻器.电源电动势E=12 V,内阻为r=1.0 Ω.一质量 m=20 g的金属棒ab与两导轨垂直并接触良好.整个装置处于磁感应强度B=0.80 T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计).金属导轨是光滑的,g取10 m/s2,要保持金属棒在导轨上静止,求:
/
(1)金属棒所受到的安培力;
(2)通过金属棒的电流;
(3)滑动变阻器R接入到电路中的阻值.
解析:(1)F=mgsin 30°
F=0.1 N.
(2)金属棒静止在金属轨道上受力平衡,
/
如图所示
解得I=
??
????
=0.5 A.
(3)设变阻器接入电路的阻值为R,根据闭合电路欧姆定律E=I(R+r)
解得R=
??
??
???=23 Ω.
答案:(1)0.1 N (2)0.5 A (3)23 Ω
/14.(10分)如图所示,在半径R的圆形区域内,分布着磁感应强度大小为B的匀强磁场.在圆心处发射一个运动方向与磁场垂直的电子,电子质量为m,电荷量为e.求这个电子要穿离此磁场区域应具有的最小动能.
/
解析:电子刚好不穿离磁场区域的条件是其轨迹正好和圆相切,故电子运动的半径r=
1
2
??.0①
电子做圆周运动的向心力由洛伦兹力提供,即evB=
??
??
2
??
0②
而动能Ek=
1
2
??
??
2
0③
三式联立可得Ek=
??
2
??
2
??
2
8??
.
答案:
??
2
??
2
??
2
8??
/15.(12分)如图所示,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m、电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.
/
(1)求小滑块运动到C点时的速度大小vC;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点.已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vP.
解析:(1)小滑块沿MN运动过程,水平方向受力满足
qvB+N=qE
小滑块在C点离开MN时N=0
解得vC=
??
??
.
(2)由动能定理mgh-Wf=
1
2
??
??
??
2
?0
解得Wf=mgh?
??
??
2
2
??
2
.
/
(3)如图,小滑块速度最大时,速度方向与电场力、重力的合力方向垂直.撤去磁场后小滑块将做类平抛运动,等效加速度为g'
g'=
????
??
2
+
??
2
且
??
??
2
=
??
??
2
+
??′
2
??
2
解得
vP=
??
??
2
+
????
??
2
+
??
2
??
2
.
答案:(1)
??
??
(2)??????
??
??
2
2
??
2
(3)
??
??
2
+
????
??
2
+
??
2
??
2
/16.(14分)(2018·全国Ⅱ卷)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示:中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l',电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行,一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出.不计重力.
/
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为
π
6
,求该粒子的比荷及其从??点运动到??点的时间.
解析:(1)粒子运动的轨迹如图甲所示.(粒子在电场中的轨迹为抛物线,在磁场中为圆弧,上下对称)
/
甲
/
乙
(2)粒子从电场下边界入射后在电场中做类平抛运动.设粒子从M点射入时速度的大小为v0,在下侧电场中运动的时间为t,加速度的大小为a;粒子进入磁场的速度大小为v,方向与电场方向的夹角为θ(见图乙),速度沿电场方向的分量为v1,根据牛顿第二定律有
qE=ma①
式中q和m分别为粒子的电荷量和质量.由运动学公式有
v1=at②
l'=v0t③
v1=vcos θ④
粒子在磁场中做匀速圆周运动,设其运动轨道半径为R,由洛伦兹力公式和牛顿第二定律得
qvB=
??
??
2
??
0⑤
由几何关系得l=2Rcos θ⑥
联立①②③④⑤⑥式得v0=
2????'
????
.0⑦
(3)由运动学公式和题给数据得
v1=v0cot
π
6
⑧
联立①②③⑦⑧式得
??
??
=
4
3
????'
??
2
??
2
0⑨
设粒子由M点运动到N点所用的时间为t',则
t'=2t+
2
π
2
-
π
6
2π
??0⑩
式中T是粒子在磁场中做匀速圆周运动的周期,
T=
2π??
????
/
由③⑦⑨⑩/式得
t'=
????
??
1+
3
π??
18??'
.0/
答案:(1)见解析图 (2)
2????'
????
(3)
4
3
????'
??
2
??
2
????
??
1+
3
π??
18??'
同课章节目录
