六年级上册数学第1单元:2长方体和正方体的表面积课件(共26张ppt)
文档属性
| 名称 | 六年级上册数学第1单元:2长方体和正方体的表面积课件(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-05 13:52:56 | ||
图片预览




文档简介
(共26张PPT)
2
长方体和正方体的表面积(教材P6~7)
六年级数学·上
新课标[江苏]
第1单元
3cm
4cm
5cm
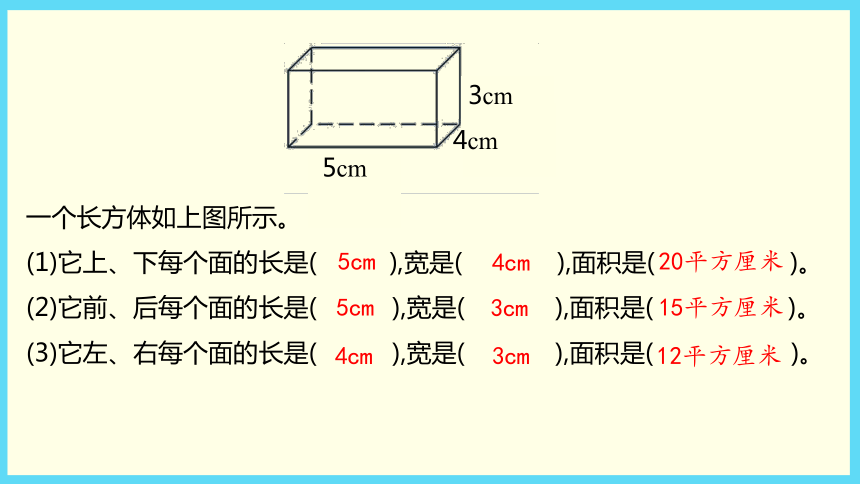
一个长方体如上图所示。
(1)它上、下每个面的长是(
),宽是(
),面积是(
)。
(2)它前、后每个面的长是( ),宽是(
),面积是(
)。
(3)它左、右每个面的长是( ),宽是(
),面积是(
)。
5cm
4cm
20平方厘米
5cm
3cm
15平方厘米
4cm
3cm
12平方厘米
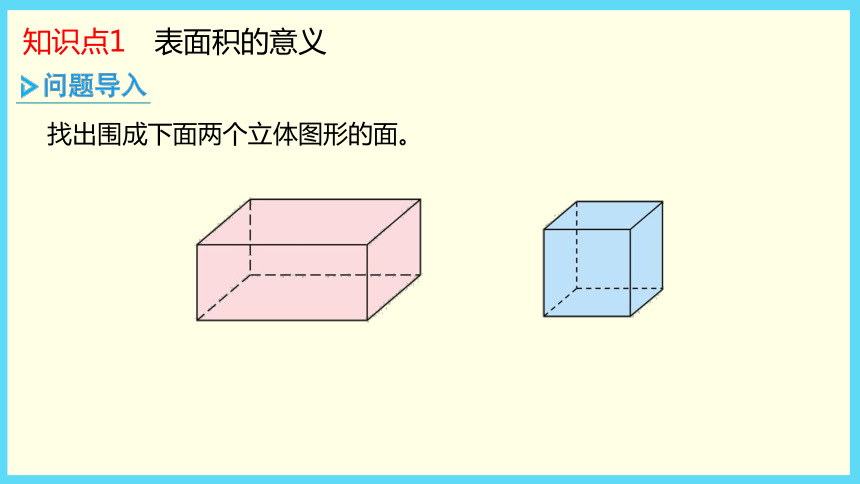
知识点1 表面积的意义
找出围成下面两个立体图形的面。
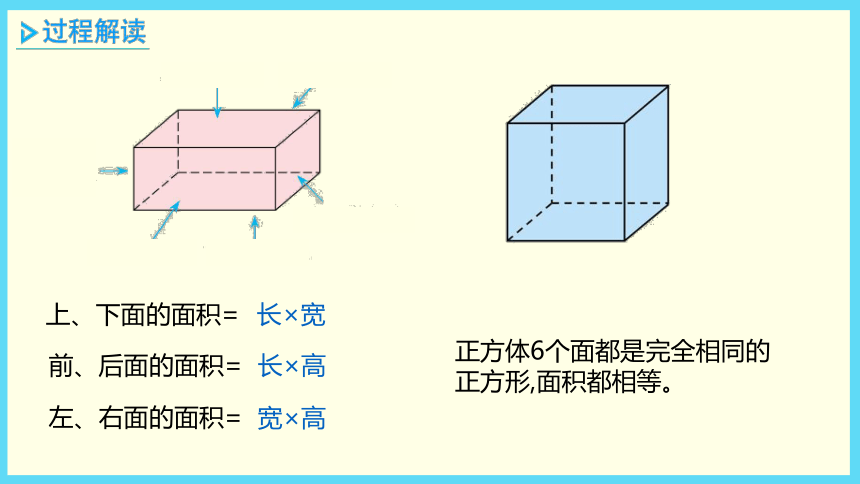
正方体6个面都是完全相同的正方形,面积都相等。
上、下面的面积=
左、右面的面积=
前、后面的面积=
长×宽
宽×高
长×高
物体表面的总面积叫作物体的表面积。
长方体(或正方体)6个面的总面积叫作它的表面积。
知识点2 长方体表面积的计算
4
做一个长6厘米、宽5厘米、高4厘米的长方体纸盒,至少要用硬纸板多少平方厘米?
求至少要用硬纸板多少平方厘米,就是求长方体几个面面积的和?你准备怎样计算?
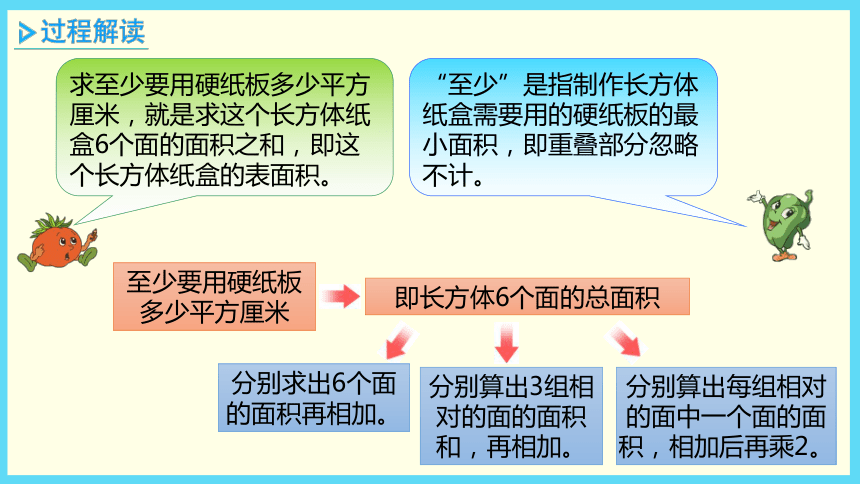
求至少要用硬纸板多少平方厘米,就是求这个长方体纸盒6个面的面积之和,即这个长方体纸盒的表面积。
“至少”是指制作长方体纸盒需要用的硬纸板的最小面积,即重叠部分忽略不计。
至少要用硬纸板多少平方厘米
即长方体6个面的总面积
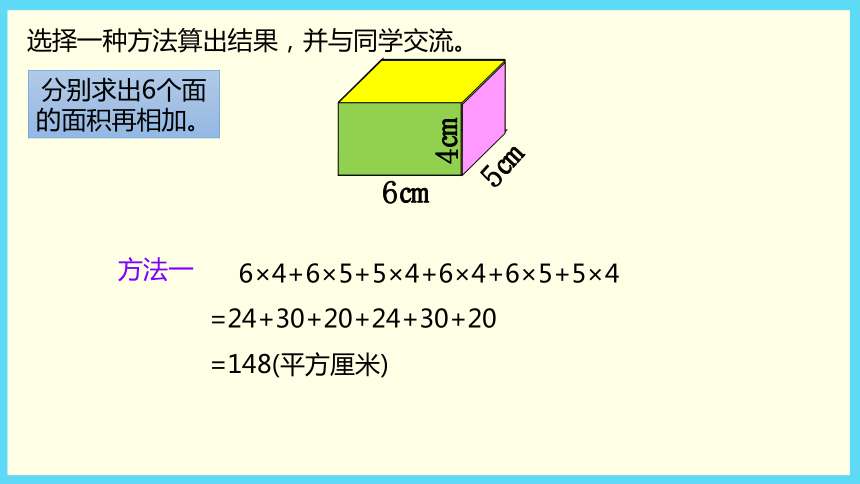
分别求出6个面的面积再相加。
分别算出3组相对的面的面积和,再相加。
分别算出每组相对的面中一个面的面积,相加后再乘2。
选择一种方法算出结果,并与同学交流。
方法一
6×4+6×5+5×4+6×4+6×5+5×4
=24+30+20+24+30+20
=148(平方厘米)
5㎝
6㎝
4㎝
分别求出6个面的面积再相加。
5㎝
4㎝
5㎝
4㎝
4㎝
5㎝
方法二
6×4×2+5×4×2+6×5×2
=48+40+60
=148(平方厘米)
6㎝
6㎝
6㎝
分别算出3组相对的面的面积和,再相加。
5㎝
4㎝
方法三
(6×4+5×4+6×5)×2
=(24+20+30)×2
=74×2
=148(平方厘米)
6㎝
分别算出每组相对的面中一个面的面积,相加后再乘2。
如果所求长方体的表面积是6个面的面积时,用方法三计算会比较简便哟!
1.长方体表面积常用的计算方法:长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2
2.如果用S表示长方体的表面积,用a,b,h分别表示长方体的长、宽、高,那么长方体表面积的计算公式可表示为S=(ab+ah+bh)×2。
知识点3 正方体表面积的计算
做一个棱长3分米的正方体纸盒,至少要用硬纸板多少平方分米
读题后要先明确所求表面积包含哪几个面的面积,再计算。
求至少要用多少硬纸板,就是求这个正方体纸盒6个面的总面积,即它的表面积。
求至少要用硬纸板多少平方分米
即正方体6个面的总面积
一个面的面积×6
6个面完全相同
一个面怎么求?
3×3×6=54(平方分米)
答:至少要用硬纸板54平方分米。
正方体的表面积=棱长×棱长×6,如果用S表示正方体的表面积,用a表示正方体的棱长,那么正方体表面积的计算公式可表示为S=6a2。
正方体6个面是相同的正方形,所以表面积=每个面的面积×6。
知识点4 应用表面积计算方法解决实际问题
5
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
求需要玻璃多少平方分米,就是求长方体哪几个面面积的和?可以怎样计算?
5
制作这个鱼缸至少需要玻璃多少平方分米?
5个面,少上面的面。
求制作这个鱼缸至少需要玻璃多少平方分米,实际就是求这个长方体鱼缸的表面积。
鱼缸无盖,就是求鱼缸前、后、左、右和下面5个面的面积和。
方法一 (前面面积+左面面积)×2+下面面积=鱼缸的表面积。
方法二 (前面面积+左面面积+上面面积)×2-上面面积=鱼缸的表面积。
方法三 依据展开图求总面积,展开图如下图所示。
利用展开图求长方体的表面积时,展开图的形状不同,求面积的方法也就不同。
5
选择一种方法算出结果,与同学交流。
方法一 (5×3.5+3×3.5)×2+5×3
=56+15
=71(平方分米)
方法二 (5×3.5+3×3.5+3×5)×2-3×5
=86-15
=71(平方分米)
方法三 (5+3.5×2)×3+5×3.5×2
=36+35
=71(平方分米)
答:至少需要玻璃
平方分米。
71
还有其他的方法吗?
5×3+5×3.5×2+3×3.5×2
=15+35+21
=71(平方分米)
在实际生活中,并不是所有长方体都有6个面,长方体(或正方体)的水池、鱼缸等只有5个面,通风管只有4个面,在计算时应根据实际条件和题中的要求解题。
用计算长方体表面积的方法解决实际问题时,要注意什么?
在运用长方体和正方体的表面积解决生活中的实际问题时,要根据实际问题确定计算哪几个面面积的和。
另外,可以根据长方体面的特征,用不同的方法计算。
1.
李大叔家挖了一个长方形的蓄水池,从里面量,长3.5米,宽2米,深1.5米。
(1)这个蓄水池占地多少平方米?
【思路导引】把这个蓄水池看成一个长方体,求这个蓄水池占地面积就是求这个长方体的下面的面积,用长乘宽。
3.5×2=7(平方米)
答:这个蓄水池占地7平方米。
1.
李大叔家挖了一个长方形的蓄水池,从里面量,长3.5米,
宽2米,深1.5米。
(2)在蓄水池的四周和底面抹水泥,抹水泥的面积是多少平方米?
【思路导引】抹水泥的面积就等于长方体的表面积减去上面的面积,即S=(ab+bh+ah)×2-ab。
(3.5×2+3.5×1.5+2×1.5)×2-3.5×2
=(7+5.25+3)×2-7
=30.5-7
=23.5(平方米)
答:抹水泥的面积是23.5平方米。
2.一个正方体,它们棱的总长是24厘米,那么正方体的表面积是( )。
A.2平方厘米
B.24平方厘米
C.16平方厘米
3.明明用1立方厘米的小正方体摆成一个长方体,从正面、左面和上面看到的分别是如图所示的图形,这个长方体的表面积是( )平方厘米。
A.52
B.26
C.24
前面
右面
上面
A
B
小魔方
再
见
2
长方体和正方体的表面积(教材P6~7)
六年级数学·上
新课标[江苏]
第1单元
3cm
4cm
5cm
一个长方体如上图所示。
(1)它上、下每个面的长是(
),宽是(
),面积是(
)。
(2)它前、后每个面的长是( ),宽是(
),面积是(
)。
(3)它左、右每个面的长是( ),宽是(
),面积是(
)。
5cm
4cm
20平方厘米
5cm
3cm
15平方厘米
4cm
3cm
12平方厘米
知识点1 表面积的意义
找出围成下面两个立体图形的面。
正方体6个面都是完全相同的正方形,面积都相等。
上、下面的面积=
左、右面的面积=
前、后面的面积=
长×宽
宽×高
长×高
物体表面的总面积叫作物体的表面积。
长方体(或正方体)6个面的总面积叫作它的表面积。
知识点2 长方体表面积的计算
4
做一个长6厘米、宽5厘米、高4厘米的长方体纸盒,至少要用硬纸板多少平方厘米?
求至少要用硬纸板多少平方厘米,就是求长方体几个面面积的和?你准备怎样计算?
求至少要用硬纸板多少平方厘米,就是求这个长方体纸盒6个面的面积之和,即这个长方体纸盒的表面积。
“至少”是指制作长方体纸盒需要用的硬纸板的最小面积,即重叠部分忽略不计。
至少要用硬纸板多少平方厘米
即长方体6个面的总面积
分别求出6个面的面积再相加。
分别算出3组相对的面的面积和,再相加。
分别算出每组相对的面中一个面的面积,相加后再乘2。
选择一种方法算出结果,并与同学交流。
方法一
6×4+6×5+5×4+6×4+6×5+5×4
=24+30+20+24+30+20
=148(平方厘米)
5㎝
6㎝
4㎝
分别求出6个面的面积再相加。
5㎝
4㎝
5㎝
4㎝
4㎝
5㎝
方法二
6×4×2+5×4×2+6×5×2
=48+40+60
=148(平方厘米)
6㎝
6㎝
6㎝
分别算出3组相对的面的面积和,再相加。
5㎝
4㎝
方法三
(6×4+5×4+6×5)×2
=(24+20+30)×2
=74×2
=148(平方厘米)
6㎝
分别算出每组相对的面中一个面的面积,相加后再乘2。
如果所求长方体的表面积是6个面的面积时,用方法三计算会比较简便哟!
1.长方体表面积常用的计算方法:长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2
2.如果用S表示长方体的表面积,用a,b,h分别表示长方体的长、宽、高,那么长方体表面积的计算公式可表示为S=(ab+ah+bh)×2。
知识点3 正方体表面积的计算
做一个棱长3分米的正方体纸盒,至少要用硬纸板多少平方分米
读题后要先明确所求表面积包含哪几个面的面积,再计算。
求至少要用多少硬纸板,就是求这个正方体纸盒6个面的总面积,即它的表面积。
求至少要用硬纸板多少平方分米
即正方体6个面的总面积
一个面的面积×6
6个面完全相同
一个面怎么求?
3×3×6=54(平方分米)
答:至少要用硬纸板54平方分米。
正方体的表面积=棱长×棱长×6,如果用S表示正方体的表面积,用a表示正方体的棱长,那么正方体表面积的计算公式可表示为S=6a2。
正方体6个面是相同的正方形,所以表面积=每个面的面积×6。
知识点4 应用表面积计算方法解决实际问题
5
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
求需要玻璃多少平方分米,就是求长方体哪几个面面积的和?可以怎样计算?
5
制作这个鱼缸至少需要玻璃多少平方分米?
5个面,少上面的面。
求制作这个鱼缸至少需要玻璃多少平方分米,实际就是求这个长方体鱼缸的表面积。
鱼缸无盖,就是求鱼缸前、后、左、右和下面5个面的面积和。
方法一 (前面面积+左面面积)×2+下面面积=鱼缸的表面积。
方法二 (前面面积+左面面积+上面面积)×2-上面面积=鱼缸的表面积。
方法三 依据展开图求总面积,展开图如下图所示。
利用展开图求长方体的表面积时,展开图的形状不同,求面积的方法也就不同。
5
选择一种方法算出结果,与同学交流。
方法一 (5×3.5+3×3.5)×2+5×3
=56+15
=71(平方分米)
方法二 (5×3.5+3×3.5+3×5)×2-3×5
=86-15
=71(平方分米)
方法三 (5+3.5×2)×3+5×3.5×2
=36+35
=71(平方分米)
答:至少需要玻璃
平方分米。
71
还有其他的方法吗?
5×3+5×3.5×2+3×3.5×2
=15+35+21
=71(平方分米)
在实际生活中,并不是所有长方体都有6个面,长方体(或正方体)的水池、鱼缸等只有5个面,通风管只有4个面,在计算时应根据实际条件和题中的要求解题。
用计算长方体表面积的方法解决实际问题时,要注意什么?
在运用长方体和正方体的表面积解决生活中的实际问题时,要根据实际问题确定计算哪几个面面积的和。
另外,可以根据长方体面的特征,用不同的方法计算。
1.
李大叔家挖了一个长方形的蓄水池,从里面量,长3.5米,宽2米,深1.5米。
(1)这个蓄水池占地多少平方米?
【思路导引】把这个蓄水池看成一个长方体,求这个蓄水池占地面积就是求这个长方体的下面的面积,用长乘宽。
3.5×2=7(平方米)
答:这个蓄水池占地7平方米。
1.
李大叔家挖了一个长方形的蓄水池,从里面量,长3.5米,
宽2米,深1.5米。
(2)在蓄水池的四周和底面抹水泥,抹水泥的面积是多少平方米?
【思路导引】抹水泥的面积就等于长方体的表面积减去上面的面积,即S=(ab+bh+ah)×2-ab。
(3.5×2+3.5×1.5+2×1.5)×2-3.5×2
=(7+5.25+3)×2-7
=30.5-7
=23.5(平方米)
答:抹水泥的面积是23.5平方米。
2.一个正方体,它们棱的总长是24厘米,那么正方体的表面积是( )。
A.2平方厘米
B.24平方厘米
C.16平方厘米
3.明明用1立方厘米的小正方体摆成一个长方体,从正面、左面和上面看到的分别是如图所示的图形,这个长方体的表面积是( )平方厘米。
A.52
B.26
C.24
前面
右面
上面
A
B
小魔方
再
见
