新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.2.1-2.2.2 24张PPT
文档属性
| 名称 | 新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.2.1-2.2.2 24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 425.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 21:26:14 | ||
图片预览







文档简介
课件24张PPT。第二章 点、直线、平面之间的位置关系[必修2]2.2 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
2.2.2 平面与平面平行的判定1.文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面 .该定理常表述为:线线平行,则线面平行.?
符号语言:若a?α,b?α,且a∥b,则 .?
2.用该定理判断直线a和平面α平行时,必须具备三个条件:(1)直线a不在平面α内,即a?α;(2)直线b在平面α内,即b?α;(3)两直线a,b平行,即a∥b.三个条件缺一不可.预习探究直线与平面平行的判定定理知识点一平行a∥α预习探究[思考] 若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗?解:不一定.只有当这条直线在这个平面外时,这条直线才与这个平面平行.预习探究1.文字语言:一个平面内的两条相交直线与另一个平面平行,
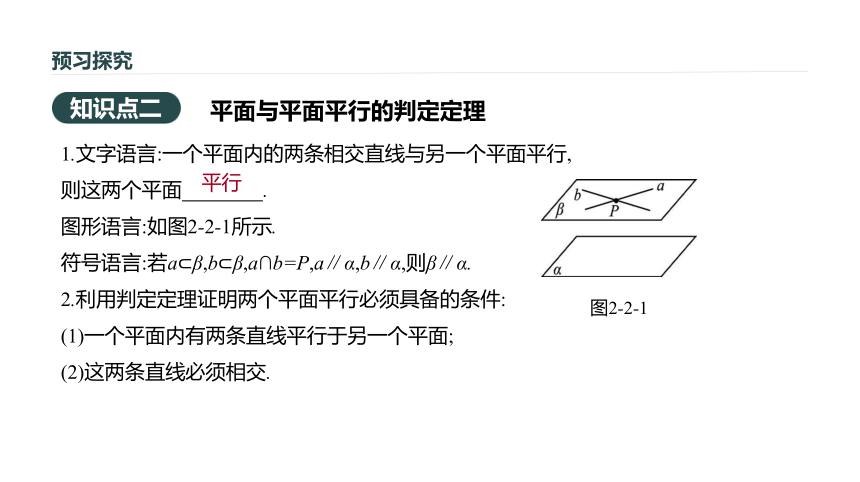
则这两个平面 .?
图形语言:如图2-2-1所示.
符号语言:若a?β,b?β,a∩b=P,a∥α,b∥α,则β∥α.
2.利用判定定理证明两个平面平行必须具备的条件:
(1)一个平面内有两条直线平行于另一个平面;
(2)这两条直线必须相交.平面与平面平行的判定定理知识点二图2-2-1平行预习探究[思考] 若两个平面平行,则这两个平面内的直线是否都平行?解:若两个平面平行,则这两个平面内的直线没有交点,所以它们只能是平行或异面.
[讨论] 如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗?解:不一定.这条直线与另一个平面平行或在另一个平面内.考点类析[导入] (1)当直线与平面的交点个数满足什么情况时,才能保证直线与平面平行?
(2)证明线面平行问题的一般思路是什么?直线与平面平行的判定考点一解:(1)当直线与平面的交点个数为0时,才能保证直线与平面平行.
(2)证明线面平行可转化成证明线线平行.考点类析例1 (1)已知P是平行四边形ABCD所在平面外的一点,Q是PA的中点,则直线PC与平面BDQ的位置关系为 ( )
A.平行 B.相交
C.在平面内 D.无法确定
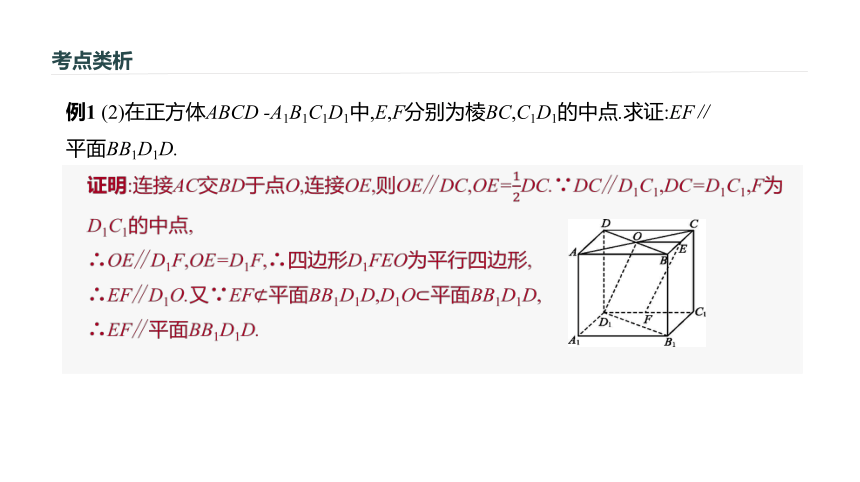
A[解析] (1)连接AC交BD于点O,连接OQ,则OA=OC.又AQ=PQ,
∴OQ∥PC.∵OQ?平面BDQ,PC?平面BDQ,∴PC∥平面BDQ.
考点类析例1 (2)在正方体ABCD -A1B1C1D1中,E,F分别为棱BC,C1D1的中点.求证:EF∥平面BB1D1D.
?考点类析变式 如图2-2-2所示,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:(1)EH∥平面BCD;
(2)BD∥平面EFGH.
证明:(1)∵EH为△ABD的中位线,∴EH∥BD.
∵EH?平面BCD,BD?平面BCD,∴EH∥平面BCD.
(2)∵BD∥EH,BD?平面EFGH,EH?平面EFGH,∴BD∥平面EFGH.图2-2-2考点类析[小结] (1)利用直线与平面平行的判定定理证明线面平行时,关键是寻找平面内与已知直线平行的直线.
(2)证明线线平行的常用方法有三角形中位线定理、平行四边形的性质、平行线分线段成比例定理、平行公理等.考点类析平面与平面平行的判定考点二 [导入] 当平面与平面的交点个数满足什么情况时,才能保证平面与平面平行?解:当平面与平面的交点个数为0时,才能保证平面与平面平行.例2(1)已知正方体ABCD -A1B1C1D1中,E,F,G分别为B1C1,A1D1,A1B1的中点,则平面EBD与平面FGA的位置关系为 .?平行考点类析例2 (2)如图2-2-3所示,在三棱柱ABC - A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
图2-2-3证明:由棱柱的性质知,B1C1∥BC,B1C1=BC,
又D,E分别为BC,B1C1的中点,
所以C1E∥DB,C1E=DB,所以四边形C1DBE为平行四边形,所以EB∥C1D.
又C1D?平面ADC1,EB?平面ADC1,所以EB∥平面ADC1.连接DE,易知EB1∥BD,EB1=BD.所以四边形EDBB1为平行四边形,则ED∥B1B,ED=B1B.考点类析例2 (2)如图2-2-3所示,在三棱柱ABC - A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
图2-2-3又A1A∥B1B,A1A=B1B,所以A1A∥ED,A1A=ED,所以四边形A1ADE为平行四边形,所以A1E∥AD.
又AD?平面ADC1,A1E?平面ADC1,所以A1E∥平面ADC1.
又A1E∩EB=E,所以平面A1EB∥平面ADC1.考点类析变式 已知四棱锥P -ABCD中,底面ABCD为平行四边形.点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
证明:∵PM∶MA=BN∶ND=PQ∶QD,∴MQ∥AD,NQ∥
BP,而BP?平面PBC,NQ?平面PBC,∴NQ∥平面PBC.又∵四边形ABCD为平行四形,∴BC∥AD,∴MQ∥BC,而BC?平面PBC,MQ?平面PBC,∴MQ∥平面PBC.易知MQ∩NQ=Q,根据平面与平面平行的判定定理,可知平面MNQ∥平面PBC.考点类析[小结] (1)要证明两平面平行,只需在其中一个平面内找到两条相交直线平行于另一个平面.
(2)判定两个平面平行与判定线面平行一样,应遵循先找后作的原则,即先在一个面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.考点类析线面平行、面面平行的综合应用考点三[导入] 证明面面平行问题的一般思路是什么?解:证明面面平行可转化成证明线面平行,进而转化成证明线线平行.考点类析例3 如图2-2-4所示,P是△ABC所在平面外的一点,A',B',C'分别是△PBC,△PCA,△PAB的重心.
(1)求证:平面ABC∥平面A'B'C';
(2)求△A'B'C'与△ABC的面积之比.
?图2-2-4考点类析例3 如图2-2-4所示,P是△ABC所在平面外的一点,A',B',C'分别是△PBC,△PCA,△PAB的重心.
(1)求证:平面ABC∥平面A'B'C';
(2)求△A'B'C'与△ABC的面积之比.
图2-2-4考点类析变式 如图2-2-5所示,已知正方体ABCD -A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
证明:(1)∵B1B∥DD1,B1B=D1D,∴四边形BB1D1D是平行四边形,∴B1D1∥BD,又BD?平面B1D1C,B1D1?平面B1D1C,∴BD∥平面B1D1C.同理,A1D∥平面B1D1C.又∵A1D∩BD=D,A1D,BD?平面A1BD,∴平面A1BD∥平面B1D1C.图2-2-5考点类析变式 如图2-2-5所示,已知正方体ABCD -A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
考点类析[小结] 面面平行问题常常转化为线面平行问题,而线面平行问题又可以转化为线线平行问题,所以需注意转化思想的运用.当堂自测[解析]
∵AE∶EB=CF∶FB=1∶3,∴AC∥EF.∵AC?平面DEF,EF?平面DEF,∴AC∥平面DEF.
1.点P是平面α外一点,过点P且平行于平面α的平面有( )
A.0个 B.1个 C.2个 D.无数个B2.在空间四边形ABCD中,E,F分别是AB,BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是 ( )
A.平行 B.相交
C.在平面内 D.不能确定A当堂自测3.一块矩形木板ABCD的一边AB在平面α内,把这块矩形木板绕AB转动,在转动的过程中,AB的对边CD与平面α的位置关系是 .?CD∥α或CD?α[解析] 在转动过程中CD∥AB,由直线与平面平行的判定定理得CD∥α或CD?α.
当堂自测4.如图2-2-6所示,在正方体ABCD -A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,若Q是CC1的中点.证明:平面D1BQ∥平面PAO.证明: ∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.∵P,O分别为DD1,DB的中点,∴D1B∥PO.又∵D1B?平面PAO,PO?平面PAO,QB?平面PAO,PA?平面PAO,
∴D1B∥平面PAO,QB∥平面PAO.
又D1B∩QB=B,D1B,QB?平面D1BQ,
∴平面D1BQ∥平面PAO.图2-2-6
2.2.1 直线与平面平行的判定
2.2.2 平面与平面平行的判定1.文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面 .该定理常表述为:线线平行,则线面平行.?
符号语言:若a?α,b?α,且a∥b,则 .?
2.用该定理判断直线a和平面α平行时,必须具备三个条件:(1)直线a不在平面α内,即a?α;(2)直线b在平面α内,即b?α;(3)两直线a,b平行,即a∥b.三个条件缺一不可.预习探究直线与平面平行的判定定理知识点一平行a∥α预习探究[思考] 若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗?解:不一定.只有当这条直线在这个平面外时,这条直线才与这个平面平行.预习探究1.文字语言:一个平面内的两条相交直线与另一个平面平行,
则这两个平面 .?
图形语言:如图2-2-1所示.
符号语言:若a?β,b?β,a∩b=P,a∥α,b∥α,则β∥α.
2.利用判定定理证明两个平面平行必须具备的条件:
(1)一个平面内有两条直线平行于另一个平面;
(2)这两条直线必须相交.平面与平面平行的判定定理知识点二图2-2-1平行预习探究[思考] 若两个平面平行,则这两个平面内的直线是否都平行?解:若两个平面平行,则这两个平面内的直线没有交点,所以它们只能是平行或异面.
[讨论] 如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗?解:不一定.这条直线与另一个平面平行或在另一个平面内.考点类析[导入] (1)当直线与平面的交点个数满足什么情况时,才能保证直线与平面平行?
(2)证明线面平行问题的一般思路是什么?直线与平面平行的判定考点一解:(1)当直线与平面的交点个数为0时,才能保证直线与平面平行.
(2)证明线面平行可转化成证明线线平行.考点类析例1 (1)已知P是平行四边形ABCD所在平面外的一点,Q是PA的中点,则直线PC与平面BDQ的位置关系为 ( )
A.平行 B.相交
C.在平面内 D.无法确定
A[解析] (1)连接AC交BD于点O,连接OQ,则OA=OC.又AQ=PQ,
∴OQ∥PC.∵OQ?平面BDQ,PC?平面BDQ,∴PC∥平面BDQ.
考点类析例1 (2)在正方体ABCD -A1B1C1D1中,E,F分别为棱BC,C1D1的中点.求证:EF∥平面BB1D1D.
?考点类析变式 如图2-2-2所示,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:(1)EH∥平面BCD;
(2)BD∥平面EFGH.
证明:(1)∵EH为△ABD的中位线,∴EH∥BD.
∵EH?平面BCD,BD?平面BCD,∴EH∥平面BCD.
(2)∵BD∥EH,BD?平面EFGH,EH?平面EFGH,∴BD∥平面EFGH.图2-2-2考点类析[小结] (1)利用直线与平面平行的判定定理证明线面平行时,关键是寻找平面内与已知直线平行的直线.
(2)证明线线平行的常用方法有三角形中位线定理、平行四边形的性质、平行线分线段成比例定理、平行公理等.考点类析平面与平面平行的判定考点二 [导入] 当平面与平面的交点个数满足什么情况时,才能保证平面与平面平行?解:当平面与平面的交点个数为0时,才能保证平面与平面平行.例2(1)已知正方体ABCD -A1B1C1D1中,E,F,G分别为B1C1,A1D1,A1B1的中点,则平面EBD与平面FGA的位置关系为 .?平行考点类析例2 (2)如图2-2-3所示,在三棱柱ABC - A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
图2-2-3证明:由棱柱的性质知,B1C1∥BC,B1C1=BC,
又D,E分别为BC,B1C1的中点,
所以C1E∥DB,C1E=DB,所以四边形C1DBE为平行四边形,所以EB∥C1D.
又C1D?平面ADC1,EB?平面ADC1,所以EB∥平面ADC1.连接DE,易知EB1∥BD,EB1=BD.所以四边形EDBB1为平行四边形,则ED∥B1B,ED=B1B.考点类析例2 (2)如图2-2-3所示,在三棱柱ABC - A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
图2-2-3又A1A∥B1B,A1A=B1B,所以A1A∥ED,A1A=ED,所以四边形A1ADE为平行四边形,所以A1E∥AD.
又AD?平面ADC1,A1E?平面ADC1,所以A1E∥平面ADC1.
又A1E∩EB=E,所以平面A1EB∥平面ADC1.考点类析变式 已知四棱锥P -ABCD中,底面ABCD为平行四边形.点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
证明:∵PM∶MA=BN∶ND=PQ∶QD,∴MQ∥AD,NQ∥
BP,而BP?平面PBC,NQ?平面PBC,∴NQ∥平面PBC.又∵四边形ABCD为平行四形,∴BC∥AD,∴MQ∥BC,而BC?平面PBC,MQ?平面PBC,∴MQ∥平面PBC.易知MQ∩NQ=Q,根据平面与平面平行的判定定理,可知平面MNQ∥平面PBC.考点类析[小结] (1)要证明两平面平行,只需在其中一个平面内找到两条相交直线平行于另一个平面.
(2)判定两个平面平行与判定线面平行一样,应遵循先找后作的原则,即先在一个面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.考点类析线面平行、面面平行的综合应用考点三[导入] 证明面面平行问题的一般思路是什么?解:证明面面平行可转化成证明线面平行,进而转化成证明线线平行.考点类析例3 如图2-2-4所示,P是△ABC所在平面外的一点,A',B',C'分别是△PBC,△PCA,△PAB的重心.
(1)求证:平面ABC∥平面A'B'C';
(2)求△A'B'C'与△ABC的面积之比.
?图2-2-4考点类析例3 如图2-2-4所示,P是△ABC所在平面外的一点,A',B',C'分别是△PBC,△PCA,△PAB的重心.
(1)求证:平面ABC∥平面A'B'C';
(2)求△A'B'C'与△ABC的面积之比.
图2-2-4考点类析变式 如图2-2-5所示,已知正方体ABCD -A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
证明:(1)∵B1B∥DD1,B1B=D1D,∴四边形BB1D1D是平行四边形,∴B1D1∥BD,又BD?平面B1D1C,B1D1?平面B1D1C,∴BD∥平面B1D1C.同理,A1D∥平面B1D1C.又∵A1D∩BD=D,A1D,BD?平面A1BD,∴平面A1BD∥平面B1D1C.图2-2-5考点类析变式 如图2-2-5所示,已知正方体ABCD -A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
考点类析[小结] 面面平行问题常常转化为线面平行问题,而线面平行问题又可以转化为线线平行问题,所以需注意转化思想的运用.当堂自测[解析]
∵AE∶EB=CF∶FB=1∶3,∴AC∥EF.∵AC?平面DEF,EF?平面DEF,∴AC∥平面DEF.
1.点P是平面α外一点,过点P且平行于平面α的平面有( )
A.0个 B.1个 C.2个 D.无数个B2.在空间四边形ABCD中,E,F分别是AB,BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是 ( )
A.平行 B.相交
C.在平面内 D.不能确定A当堂自测3.一块矩形木板ABCD的一边AB在平面α内,把这块矩形木板绕AB转动,在转动的过程中,AB的对边CD与平面α的位置关系是 .?CD∥α或CD?α[解析] 在转动过程中CD∥AB,由直线与平面平行的判定定理得CD∥α或CD?α.
当堂自测4.如图2-2-6所示,在正方体ABCD -A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,若Q是CC1的中点.证明:平面D1BQ∥平面PAO.证明: ∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.∵P,O分别为DD1,DB的中点,∴D1B∥PO.又∵D1B?平面PAO,PO?平面PAO,QB?平面PAO,PA?平面PAO,
∴D1B∥平面PAO,QB∥平面PAO.
又D1B∩QB=B,D1B,QB?平面D1BQ,
∴平面D1BQ∥平面PAO.图2-2-6
同课章节目录
