新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.2.3-2.2.4 23张PPT
文档属性
| 名称 | 新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.2.3-2.2.4 23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 21:26:00 | ||
图片预览







文档简介
课件23张PPT。第二章 点、直线、平面之间的位置关系[必修2]2.2.3 直线与平面平行的性质
2.2.4 平面与平面平行的性质预习探究直线和平面平行的性质定理知识点一平行平行线线平行预习探究[思考] 如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?解:平行或异面,如图所示:预习探究[讨论] (1)若直线a∥平面α,则直线a平行于平面α内的任意一条直线,对吗?
(2)若直线a与平面α不平行,则直线a就与平面α内的任意一条直线都不平行,对吗?解:(1)不对.若直线a∥平面α,则由线面平行的性质定理可知直线a与平面α内的一组直线平行.
(2)不对.若直线a与平面α不平行,则直线a与平面α相交或a?α.当a?α时,α内有无数条直线与直线a平行.预习探究两个平面平行的性质定理知识点二平行平行线线平行预习探究[讨论] (1)若两个平面平行,那么两个平面内的所有直线都相互平行吗?
(2)若两个平面平行,其中一个平面内的直线必平行于另一个平面吗?解:(1)不一定.因为两个平面平行,所以分别在两个平面内的两条直线无公共点,它们平行或异面.
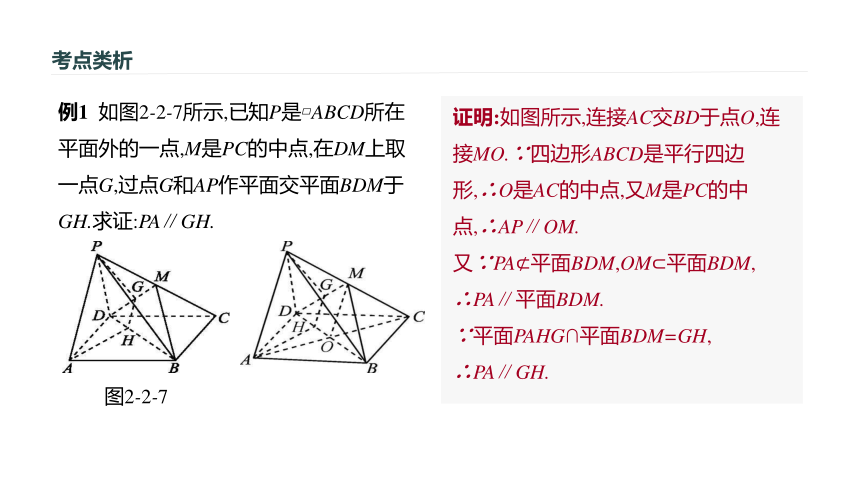
(2)平行.因为两个平面平行,所以这两个平面无公共点,所以其中一个平面内的直线必和另一个平面无公共点,所以它们平行.考点类析[导入] 证明直线与直线平行的思路有哪些?证明直线与直线平行考点一解:(1)利用直线与平面平行的性质定理.(2)利用两个平面平行的性质定理.(3)利用公理4.考点类析例1 如图2-2-7所示,已知P是?ABCD所在平面外的一点,M是PC的中点,在DM上取一点G,过点G和AP作平面交平面BDM于GH.求证:PA∥GH.
证明:如图所示,连接AC交BD于点O,连接MO.∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴AP∥OM.
又∵PA?平面BDM,OM?平面BDM,
∴PA∥平面BDM.
∵平面PAHG∩平面BDM=GH,
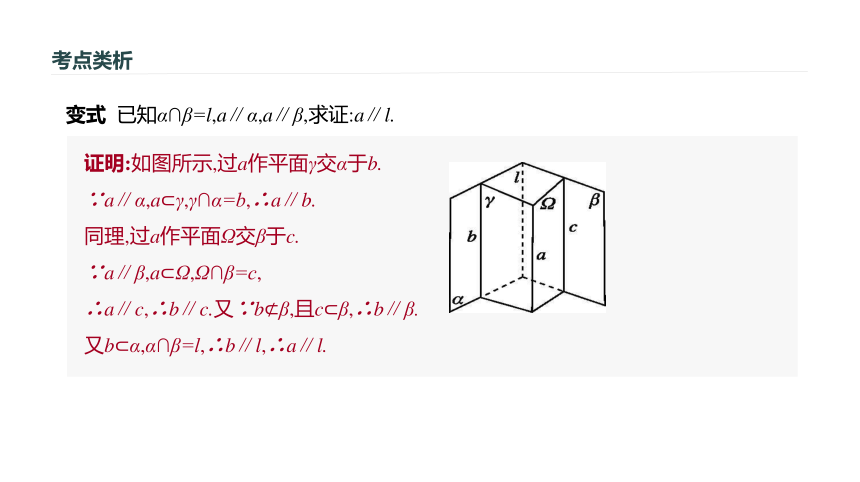
∴PA∥GH.图2-2-7考点类析变式 已知α∩β=l,a∥α,a∥β,求证:a∥l.
证明:如图所示,过a作平面γ交α于b.
∵a∥α,a?γ,γ∩α=b,∴a∥b.
同理,过a作平面Ω交β于c.
∵a∥β,a?Ω,Ω∩β=c,
∴a∥c,∴b∥c.又∵b?β,且c?β,∴b∥β.
又b?α,α∩β=l,∴b∥l,∴a∥l.考点类析[小结] 在将线面平行转化为线线平行时,注意观察图形中是不是具有性质定理中所要求的平面.考点类析证明直线与平面平行考点二例2 如图2-2-8所示,在直三棱柱ABC -A1B1C1中,若D是AB的中点,则直线AC1与平面CDB1的关系为 ( )
A.AC1∥平面CDB1
B.AC1在平面CDB1中
C.AC1与平面CDB1相交
D.无法判断关系
A图2-2-8考点类析变式 如图2-2-9所示,平行四边形EFGH的顶点分别在空间四边形ABCD的各边上,求证:BD∥平面EFGH.
证明:∵EH∥FG,EH?平面BCD,FG?平面BCD,∴EH∥平面BCD.
又∵EH?平面ABD,平面BCD∩平面ABD=BD,∴EH∥BD.
∵EH?平面EFGH,BD?平面EFGH,∴BD∥平面EFGH.图2-2-9考点类析[小结] 线面平行的性质和判定定理经常交替使用,也就是通过线线平行得到线面平行,再通过线面平行得到线线平行.利用线面平行的性质定理解题的具体步骤:(1)确定(或寻找)一条直线平行于一个平面;(2)确定(或寻找)过这条直线且与这个平行平面相交的平面;(3)确定交线;(4)由性质定理得出线线平行的结论.考点类析拓展 已知:a,b是异面直线.
求证:过b有且只有一个平面与a平行.
证明:(1)存在性.如图所示,
在直线b上任取一点A,显然A?a.
过点A与直线a作平面β,在平面β内过点A作直线a'∥a,则a'与b是相交直线,它们可以确定一个平面α,
∵b?α,a与b异面,∴a?α.
又∵a∥a',a'?α,∴a∥α,∴过b有一个平面α与a平行.
考点类析拓展 已知:a,b是异面直线.
求证:过b有且只有一个平面与a平行.
(2)唯一性.
假设平面γ是过b且与a平行的另一个平面,则b?γ.
∵A∈b,∴A∈γ.又∵A∈β,∴γ与β相交,设交线为a″,则A∈a″.
∵a∥γ,a?β,γ∩β=a″,∴a∥a″.又a∥a',∴a'∥a″,这与a'∩a″=A矛盾.
∴假设错误,故过b且与a平行的平面只有一个.
综上所述,过b有且只有一个平面与a平行.考点类析平行关系的综合应用考点三[导入] 三种平行关系之间的相互转化关系如何?解:三种平行关系可以任意转化,其相互转化关系如图所示.考点类析例3 如图2-2-10所示,在棱长为2的正方体ABCD - A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.
?图2-2-10考点类析例3 如图2-2-10所示,在棱长为2的正方体ABCD - A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.
?图2-2-10考点类析变式 如图2-2-11所示,三棱锥A - BCD被一平面所截,截面为平行四边形EFGH.求证:CD∥平面EFGH.
证明:∵四边形EFGH是平行四边形,∴EF∥GH.
∵EF?平面BCD,GH?平面BCD,∴EF∥平面BCD.
又∵EF?平面ACD,平面ACD∩平面BCD=CD,∴EF∥CD.
又∵EF?平面EFGH,CD?平面EFGH,∴CD∥平面EFGH.图2-2-11考点类析[小结] 利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作平面的交线,往往需要有三个平面,即有两个平行平面,再构造第三个平面与两平行平面都相交.当堂自测1.如果直线a∥平面α,b?α,那么a与b的位置关系是 ( )
A.相交 B.平行或异面
C.平行 D.异面B2.平面α与圆台的上、下底面分别相交于直线m,n,则m,n的位置关系是 ( )
A.相交 B.异面
C.平行 D.平行或异面C当堂自测3.如图2-2-12所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是平行四边形B图2-2-12当堂自测4.如图2-2-13所示,四边形ABCD是梯形,AB∥CD,且AB∥平面α,AD,BC与平面α分别交于点M,N,且M是AD的中点,AB=4,CD=6,则MN= .?5[解析] 因为AB∥平面α,AB?平面ABCD,平面ABCD∩平面α=MN,所以AB∥MN.又M是AD的中点,所以MN是梯形ABCD的中位线,故MN=5.图2-2-13
2.2.4 平面与平面平行的性质预习探究直线和平面平行的性质定理知识点一平行平行线线平行预习探究[思考] 如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?解:平行或异面,如图所示:预习探究[讨论] (1)若直线a∥平面α,则直线a平行于平面α内的任意一条直线,对吗?
(2)若直线a与平面α不平行,则直线a就与平面α内的任意一条直线都不平行,对吗?解:(1)不对.若直线a∥平面α,则由线面平行的性质定理可知直线a与平面α内的一组直线平行.
(2)不对.若直线a与平面α不平行,则直线a与平面α相交或a?α.当a?α时,α内有无数条直线与直线a平行.预习探究两个平面平行的性质定理知识点二平行平行线线平行预习探究[讨论] (1)若两个平面平行,那么两个平面内的所有直线都相互平行吗?
(2)若两个平面平行,其中一个平面内的直线必平行于另一个平面吗?解:(1)不一定.因为两个平面平行,所以分别在两个平面内的两条直线无公共点,它们平行或异面.
(2)平行.因为两个平面平行,所以这两个平面无公共点,所以其中一个平面内的直线必和另一个平面无公共点,所以它们平行.考点类析[导入] 证明直线与直线平行的思路有哪些?证明直线与直线平行考点一解:(1)利用直线与平面平行的性质定理.(2)利用两个平面平行的性质定理.(3)利用公理4.考点类析例1 如图2-2-7所示,已知P是?ABCD所在平面外的一点,M是PC的中点,在DM上取一点G,过点G和AP作平面交平面BDM于GH.求证:PA∥GH.
证明:如图所示,连接AC交BD于点O,连接MO.∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴AP∥OM.
又∵PA?平面BDM,OM?平面BDM,
∴PA∥平面BDM.
∵平面PAHG∩平面BDM=GH,
∴PA∥GH.图2-2-7考点类析变式 已知α∩β=l,a∥α,a∥β,求证:a∥l.
证明:如图所示,过a作平面γ交α于b.
∵a∥α,a?γ,γ∩α=b,∴a∥b.
同理,过a作平面Ω交β于c.
∵a∥β,a?Ω,Ω∩β=c,
∴a∥c,∴b∥c.又∵b?β,且c?β,∴b∥β.
又b?α,α∩β=l,∴b∥l,∴a∥l.考点类析[小结] 在将线面平行转化为线线平行时,注意观察图形中是不是具有性质定理中所要求的平面.考点类析证明直线与平面平行考点二例2 如图2-2-8所示,在直三棱柱ABC -A1B1C1中,若D是AB的中点,则直线AC1与平面CDB1的关系为 ( )
A.AC1∥平面CDB1
B.AC1在平面CDB1中
C.AC1与平面CDB1相交
D.无法判断关系
A图2-2-8考点类析变式 如图2-2-9所示,平行四边形EFGH的顶点分别在空间四边形ABCD的各边上,求证:BD∥平面EFGH.
证明:∵EH∥FG,EH?平面BCD,FG?平面BCD,∴EH∥平面BCD.
又∵EH?平面ABD,平面BCD∩平面ABD=BD,∴EH∥BD.
∵EH?平面EFGH,BD?平面EFGH,∴BD∥平面EFGH.图2-2-9考点类析[小结] 线面平行的性质和判定定理经常交替使用,也就是通过线线平行得到线面平行,再通过线面平行得到线线平行.利用线面平行的性质定理解题的具体步骤:(1)确定(或寻找)一条直线平行于一个平面;(2)确定(或寻找)过这条直线且与这个平行平面相交的平面;(3)确定交线;(4)由性质定理得出线线平行的结论.考点类析拓展 已知:a,b是异面直线.
求证:过b有且只有一个平面与a平行.
证明:(1)存在性.如图所示,
在直线b上任取一点A,显然A?a.
过点A与直线a作平面β,在平面β内过点A作直线a'∥a,则a'与b是相交直线,它们可以确定一个平面α,
∵b?α,a与b异面,∴a?α.
又∵a∥a',a'?α,∴a∥α,∴过b有一个平面α与a平行.
考点类析拓展 已知:a,b是异面直线.
求证:过b有且只有一个平面与a平行.
(2)唯一性.
假设平面γ是过b且与a平行的另一个平面,则b?γ.
∵A∈b,∴A∈γ.又∵A∈β,∴γ与β相交,设交线为a″,则A∈a″.
∵a∥γ,a?β,γ∩β=a″,∴a∥a″.又a∥a',∴a'∥a″,这与a'∩a″=A矛盾.
∴假设错误,故过b且与a平行的平面只有一个.
综上所述,过b有且只有一个平面与a平行.考点类析平行关系的综合应用考点三[导入] 三种平行关系之间的相互转化关系如何?解:三种平行关系可以任意转化,其相互转化关系如图所示.考点类析例3 如图2-2-10所示,在棱长为2的正方体ABCD - A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.
?图2-2-10考点类析例3 如图2-2-10所示,在棱长为2的正方体ABCD - A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.
?图2-2-10考点类析变式 如图2-2-11所示,三棱锥A - BCD被一平面所截,截面为平行四边形EFGH.求证:CD∥平面EFGH.
证明:∵四边形EFGH是平行四边形,∴EF∥GH.
∵EF?平面BCD,GH?平面BCD,∴EF∥平面BCD.
又∵EF?平面ACD,平面ACD∩平面BCD=CD,∴EF∥CD.
又∵EF?平面EFGH,CD?平面EFGH,∴CD∥平面EFGH.图2-2-11考点类析[小结] 利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作平面的交线,往往需要有三个平面,即有两个平行平面,再构造第三个平面与两平行平面都相交.当堂自测1.如果直线a∥平面α,b?α,那么a与b的位置关系是 ( )
A.相交 B.平行或异面
C.平行 D.异面B2.平面α与圆台的上、下底面分别相交于直线m,n,则m,n的位置关系是 ( )
A.相交 B.异面
C.平行 D.平行或异面C当堂自测3.如图2-2-12所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是平行四边形B图2-2-12当堂自测4.如图2-2-13所示,四边形ABCD是梯形,AB∥CD,且AB∥平面α,AD,BC与平面α分别交于点M,N,且M是AD的中点,AB=4,CD=6,则MN= .?5[解析] 因为AB∥平面α,AB?平面ABCD,平面ABCD∩平面α=MN,所以AB∥MN.又M是AD的中点,所以MN是梯形ABCD的中位线,故MN=5.图2-2-13
同课章节目录
