新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.3.1 21张PPT
文档属性
| 名称 | 新高考湖北专用 第二章 点、直线、平面之间的位置关系[必修2] 2.3.1 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 442.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 21:25:49 | ||
图片预览







文档简介
课件21张PPT。第二章 点、直线、平面之间的位置关系[必修2]2.3 直线、平面垂直的判定及其性质
2.3.1 直线与平面垂直的判定定义:如果直线l与平面α内的 一条直线都垂直,我们就说直线l与平面α互相垂直,记作 .直线l叫作平面α的垂线,平面α叫作直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫作 .?
画法:画直线和平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.预习探究直线与平面垂直的定义知识点一任意l⊥α垂足预习探究 [讨论] 直线与平面垂直定义中的关键词“任意一条直线”是否可以换成“所有直线”“无数条直线”?解:定义中的“任意一条直线”与“所有直线”是等价的,但是不可以换成“无数条直线”,因为若一条直线与某平面内无数条平行直线垂直,该直线与这个平面不一定垂直.预习探究文字语言:一条直线与一个平面内的 都垂直,则该直线与此平面垂直.?
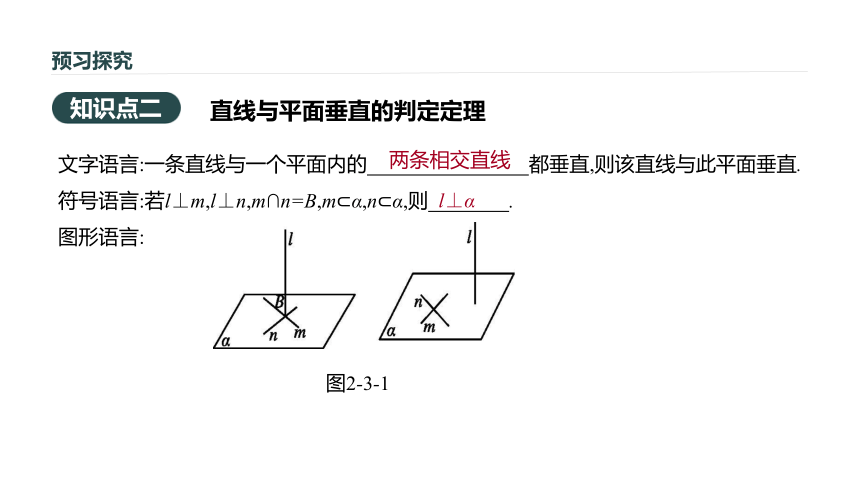
符号语言:若l⊥m,l⊥n,m∩n=B,m?α,n?α,则 .?
图形语言:直线与平面垂直的判定定理知识点二两条相交直线l⊥α图2-3-1预习探究 [思考] 线面垂直的判定定理中,平面内两条相交直线和已知直线l必须有公共点吗?解:用线面垂直的判定定理判定直线与平面垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,则是无关紧要的.预习探究1.斜线、垂线段、射影的定义
(1)斜线:一条直线和一个平面相交,但不和这个平面垂直,这条直线叫作这个平面的斜线.斜线和平面的交点叫 .?
(2)垂线段:自一点向平面引垂线,垂足是这点在这个平面上的 ,这个点和垂足间的线段叫作这点到这个平面的 .?
(3)射影:过斜线上斜足以外的一点A向平面引垂线,过垂足和斜足的直线叫作斜线在这个平面上的 .?
这里要注意两点:一是点A的任意性,可通过取不同点来说明;二是斜线在平面上的射影是过斜足和垂足的一条直线,而不是线段.直线和平面所成的角知识点三斜足射影垂线段射影预习探究2.直线和平面所成的角
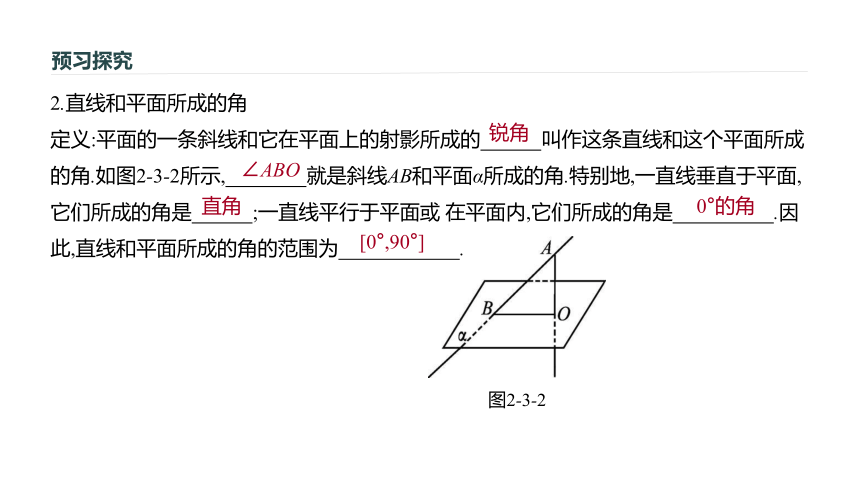
定义:平面的一条斜线和它在平面上的射影所成的 叫作这条直线和这个平面所成的角.如图2-3-2所示, 就是斜线AB和平面α所成的角.特别地,一直线垂直于平面,它们所成的角是 ;一直线平行于平面或?在平面内,它们所成的角是 .因此,直线和平面所成的角的范围为 .?图2-3-2锐角∠ABO直角0°的角[0°,90°]预习探究 [探究] 斜线与平面所成的角是否为该直线与平面内任意一条直线所成的角中最小的角?解:直线与平面所成的角是直线与其在该平面内的射影所成的角,斜线上同一点与平面内任一点的连线中,垂线段最短,即三角形的一条边不变,当另一边最短时它所对的角最小,所以斜线与平面所成的角是该直线与平面内任意一条直线所成的角中最小的角.考点类析[导入] 利用直线与平面垂直的判定定理判定直线与平面垂直的一般步骤:
①在这个平面内找两条直线,使它们和已知直线垂直;
②确定这个平面内的两条直线是相交直线;
③根据判定定理得出结论.判定直线与平面垂直考点一考点类析例1 (1)如图2-3-3所示,在正方体ABCD-A1B1C1D1中,若M为CC1的中点,AC与BD交于点O,则A1O 平面MBD.?
⊥图2-3-3考点类析例1 (2)如图2-3-4所示,在三棱柱ABC -A1B1C1中,侧棱AA1⊥底面ABC,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
时,CF⊥平面B1DF.?
a或2a?图2-3-4考点类析变式 如图2-3-5所示,直三棱柱ABC -A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,C点到AB1的距离为CE,D为AB的中点.
求证:(1)CD⊥AA1;
(2)AB1⊥平面CED.
证明:(1)由题意知AA1⊥平面ABC,CD?平面ABC,所以CD⊥AA1.
(2)因为D是AB的中点,△ABC为等腰直角三角形,∠ACB=90°,所以CD⊥AB.又CD⊥AA1,AB∩A1A=A,所以CD⊥平面A1B1BA.因为AB1?平面A1B1BA,所以CD⊥AB1.又CE⊥AB1,CD∩CE=C,所以AB1⊥平面CED.图2-3-5考点类析[小结] 证明线面垂直的方法:
(1)线线垂直证明线面垂直:
①定义法(不常用);②判定定理(最常用),要着力寻找平面内的两条相交直线(有时需要作辅助线),使它们与所给直线垂直.
(2)平行转化法(利用推论):
①a∥b,a⊥α?b⊥α;②α∥β,a⊥α?a⊥β.考点类析求直线与平面所成的角考点二 [导入] 直角三角形中,知道了三边如何求锐角的大小或三角函数值?解:先求锐角的三角函数值再求角的大小.如角的正弦值等于对边比斜边,余弦值为邻边比斜边,正切值为对边比邻边.考点类析例2 如图2-3-6所示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,且AB=BC=2,∠CBD=45°,求直线BD与平面ACD所成角的大小.
?图2-3-6考点类析变式 在三棱柱ABC -A1B1C1中,底面是正三角形,侧棱AA1⊥底面ABC,点E是侧面BB1C1C的中心,若AA1=3AB,则直线AE与平面BB1C1C所成角的大小为 .?
30° [小结] 求直线与平面所成角的步骤:(1)寻找过斜线上一点与平面垂直的直线;(2)连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角;(3)把该角归结在某个三角形中,通过解三角形,求出该角.考点类析拓展 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,A1D1的中点.
(1)求D1B与平面AC所成的角的余弦值;
(2)求EF与平面A1C1所成的角的大小.
?考点类析拓展 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,A1D1的中点.
(1)求D1B与平面AC所成的角的余弦值;
(2)求EF与平面A1C1所成的角的大小.
(2)因为E是A1A的中点,A1A⊥平面A1C1,
所以∠EFA1是EF与平面A1C1所成的角.在Rt△EA1F中,因为F是A1D1的中点,所以EA1=FA1,所以∠EFA1=45°.
故EF与平面A1C1所成的角的大小为45°.当堂自测[解析] 在空间中垂直于同一直线的两条直线可能平行、相交或异面,所以A,B错,垂直于同一直线的直线和平面的位置关系可以是直线在平面内、直线和平面平行,所以D错.
1.下列命题中正确的是 ( )
A.垂直于同一条直线的两直线平行
B.垂直于同一条直线的两直线垂直
C.垂直于同一个平面的两直线平行
D.垂直于同一条直线的一条直线和一个平面相互平行C2.直线l⊥平面α,直线m?α,则l与m不可能( )
A.平行 B.相交
C.异面 D.垂直A当堂自测[解析] 如下图所示,直线l与平面α平行或直线l与平面α垂直或直线l在平面α内都有可能.故选D.
3.直线l与平面α内的无数条直线垂直,则直线l与平面α的位置关系是 ( )
A.l与平面α平行 B.l与平面α垂直
C.l在平面α内 D.不能确定D当堂自测[解析] 由直角三角形的边角关系,可知直线与平面α所成的角为60°.
4.线段AB的长等于它在平面α内射影长的2倍,则AB所在直线与平面α所成的角为( )
A.30° B.45°
C.60° D.120°C
2.3.1 直线与平面垂直的判定定义:如果直线l与平面α内的 一条直线都垂直,我们就说直线l与平面α互相垂直,记作 .直线l叫作平面α的垂线,平面α叫作直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫作 .?
画法:画直线和平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.预习探究直线与平面垂直的定义知识点一任意l⊥α垂足预习探究 [讨论] 直线与平面垂直定义中的关键词“任意一条直线”是否可以换成“所有直线”“无数条直线”?解:定义中的“任意一条直线”与“所有直线”是等价的,但是不可以换成“无数条直线”,因为若一条直线与某平面内无数条平行直线垂直,该直线与这个平面不一定垂直.预习探究文字语言:一条直线与一个平面内的 都垂直,则该直线与此平面垂直.?
符号语言:若l⊥m,l⊥n,m∩n=B,m?α,n?α,则 .?
图形语言:直线与平面垂直的判定定理知识点二两条相交直线l⊥α图2-3-1预习探究 [思考] 线面垂直的判定定理中,平面内两条相交直线和已知直线l必须有公共点吗?解:用线面垂直的判定定理判定直线与平面垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,则是无关紧要的.预习探究1.斜线、垂线段、射影的定义
(1)斜线:一条直线和一个平面相交,但不和这个平面垂直,这条直线叫作这个平面的斜线.斜线和平面的交点叫 .?
(2)垂线段:自一点向平面引垂线,垂足是这点在这个平面上的 ,这个点和垂足间的线段叫作这点到这个平面的 .?
(3)射影:过斜线上斜足以外的一点A向平面引垂线,过垂足和斜足的直线叫作斜线在这个平面上的 .?
这里要注意两点:一是点A的任意性,可通过取不同点来说明;二是斜线在平面上的射影是过斜足和垂足的一条直线,而不是线段.直线和平面所成的角知识点三斜足射影垂线段射影预习探究2.直线和平面所成的角
定义:平面的一条斜线和它在平面上的射影所成的 叫作这条直线和这个平面所成的角.如图2-3-2所示, 就是斜线AB和平面α所成的角.特别地,一直线垂直于平面,它们所成的角是 ;一直线平行于平面或?在平面内,它们所成的角是 .因此,直线和平面所成的角的范围为 .?图2-3-2锐角∠ABO直角0°的角[0°,90°]预习探究 [探究] 斜线与平面所成的角是否为该直线与平面内任意一条直线所成的角中最小的角?解:直线与平面所成的角是直线与其在该平面内的射影所成的角,斜线上同一点与平面内任一点的连线中,垂线段最短,即三角形的一条边不变,当另一边最短时它所对的角最小,所以斜线与平面所成的角是该直线与平面内任意一条直线所成的角中最小的角.考点类析[导入] 利用直线与平面垂直的判定定理判定直线与平面垂直的一般步骤:
①在这个平面内找两条直线,使它们和已知直线垂直;
②确定这个平面内的两条直线是相交直线;
③根据判定定理得出结论.判定直线与平面垂直考点一考点类析例1 (1)如图2-3-3所示,在正方体ABCD-A1B1C1D1中,若M为CC1的中点,AC与BD交于点O,则A1O 平面MBD.?
⊥图2-3-3考点类析例1 (2)如图2-3-4所示,在三棱柱ABC -A1B1C1中,侧棱AA1⊥底面ABC,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
时,CF⊥平面B1DF.?
a或2a?图2-3-4考点类析变式 如图2-3-5所示,直三棱柱ABC -A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,C点到AB1的距离为CE,D为AB的中点.
求证:(1)CD⊥AA1;
(2)AB1⊥平面CED.
证明:(1)由题意知AA1⊥平面ABC,CD?平面ABC,所以CD⊥AA1.
(2)因为D是AB的中点,△ABC为等腰直角三角形,∠ACB=90°,所以CD⊥AB.又CD⊥AA1,AB∩A1A=A,所以CD⊥平面A1B1BA.因为AB1?平面A1B1BA,所以CD⊥AB1.又CE⊥AB1,CD∩CE=C,所以AB1⊥平面CED.图2-3-5考点类析[小结] 证明线面垂直的方法:
(1)线线垂直证明线面垂直:
①定义法(不常用);②判定定理(最常用),要着力寻找平面内的两条相交直线(有时需要作辅助线),使它们与所给直线垂直.
(2)平行转化法(利用推论):
①a∥b,a⊥α?b⊥α;②α∥β,a⊥α?a⊥β.考点类析求直线与平面所成的角考点二 [导入] 直角三角形中,知道了三边如何求锐角的大小或三角函数值?解:先求锐角的三角函数值再求角的大小.如角的正弦值等于对边比斜边,余弦值为邻边比斜边,正切值为对边比邻边.考点类析例2 如图2-3-6所示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,且AB=BC=2,∠CBD=45°,求直线BD与平面ACD所成角的大小.
?图2-3-6考点类析变式 在三棱柱ABC -A1B1C1中,底面是正三角形,侧棱AA1⊥底面ABC,点E是侧面BB1C1C的中心,若AA1=3AB,则直线AE与平面BB1C1C所成角的大小为 .?
30° [小结] 求直线与平面所成角的步骤:(1)寻找过斜线上一点与平面垂直的直线;(2)连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角;(3)把该角归结在某个三角形中,通过解三角形,求出该角.考点类析拓展 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,A1D1的中点.
(1)求D1B与平面AC所成的角的余弦值;
(2)求EF与平面A1C1所成的角的大小.
?考点类析拓展 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,A1D1的中点.
(1)求D1B与平面AC所成的角的余弦值;
(2)求EF与平面A1C1所成的角的大小.
(2)因为E是A1A的中点,A1A⊥平面A1C1,
所以∠EFA1是EF与平面A1C1所成的角.在Rt△EA1F中,因为F是A1D1的中点,所以EA1=FA1,所以∠EFA1=45°.
故EF与平面A1C1所成的角的大小为45°.当堂自测[解析] 在空间中垂直于同一直线的两条直线可能平行、相交或异面,所以A,B错,垂直于同一直线的直线和平面的位置关系可以是直线在平面内、直线和平面平行,所以D错.
1.下列命题中正确的是 ( )
A.垂直于同一条直线的两直线平行
B.垂直于同一条直线的两直线垂直
C.垂直于同一个平面的两直线平行
D.垂直于同一条直线的一条直线和一个平面相互平行C2.直线l⊥平面α,直线m?α,则l与m不可能( )
A.平行 B.相交
C.异面 D.垂直A当堂自测[解析] 如下图所示,直线l与平面α平行或直线l与平面α垂直或直线l在平面α内都有可能.故选D.
3.直线l与平面α内的无数条直线垂直,则直线l与平面α的位置关系是 ( )
A.l与平面α平行 B.l与平面α垂直
C.l在平面α内 D.不能确定D当堂自测[解析] 由直角三角形的边角关系,可知直线与平面α所成的角为60°.
4.线段AB的长等于它在平面α内射影长的2倍,则AB所在直线与平面α所成的角为( )
A.30° B.45°
C.60° D.120°C
同课章节目录
