12.1函数第2课时 函数的表示方法 课件(28张PPT)
文档属性
| 名称 | 12.1函数第2课时 函数的表示方法 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 702.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 00:00:00 | ||
图片预览






文档简介
课件28张PPT。12.1 函数第12章 一次函数第2课时 函数的表示方式1.了解并掌握函数表示方法:列表法、解析法及图象法,理解这三种表示方法的优缺点;(重点)
2. 掌握函数自变量范围的确定和函数值的求法;
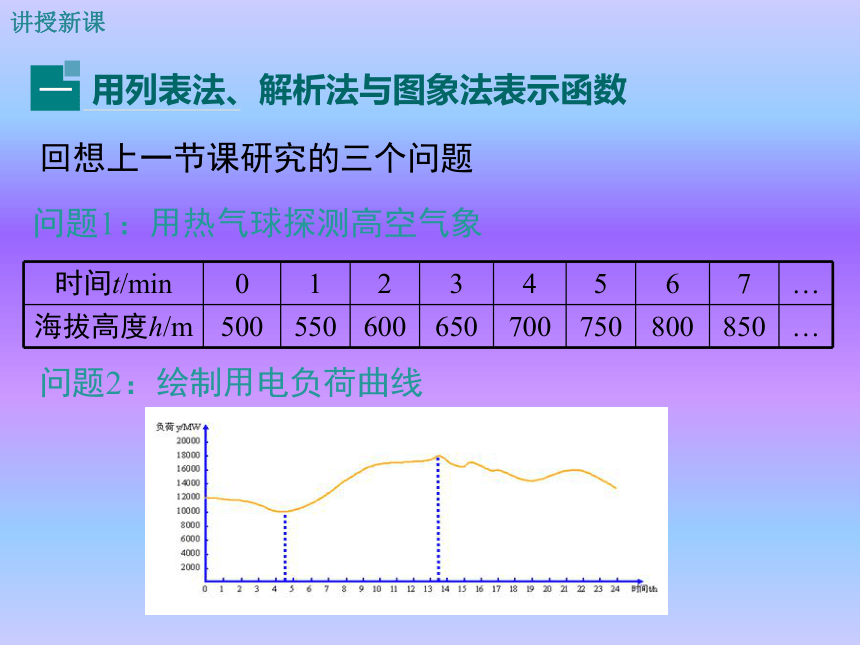
3. 能用这三种表示函数的方法解决简单的实际问题.(难点)学习目标导入新课回顾与思考下列问题中的变量y是不是x的函数?是(1) y = 2x(2) y+2x=3是不是(6)是(7) 不是(4) y=x2(5) y2=x(8) y=±x+5 (9) y=x2+3z是是不是不是(x≥0)在计算器上按照下面的程序进行操作:输入x(任意一个数)按键×2 = 显示y(计算结果)711-35207显示的数y是输入的数x的函数吗?为什么?填表:+5如果是,写出它的解析式.y = 2x+5导入新课动手操作讲授新课回想上一节课研究的三个问题问题1:用热气球探测高空气象问题2:绘制用电负荷曲线问题3:汽车刹车问题由此你发现了什么?表示函数
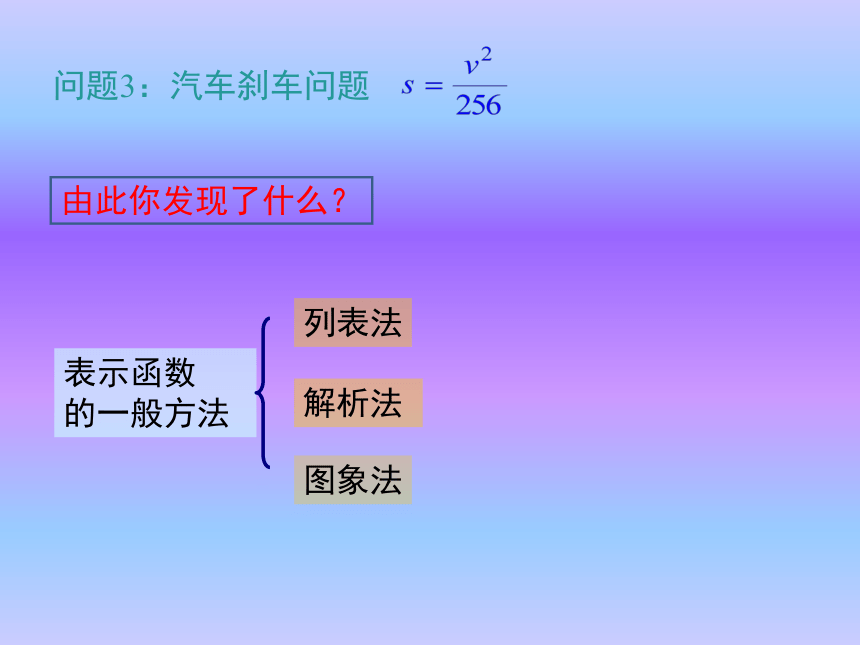
的一般方法列表法图象法解析法
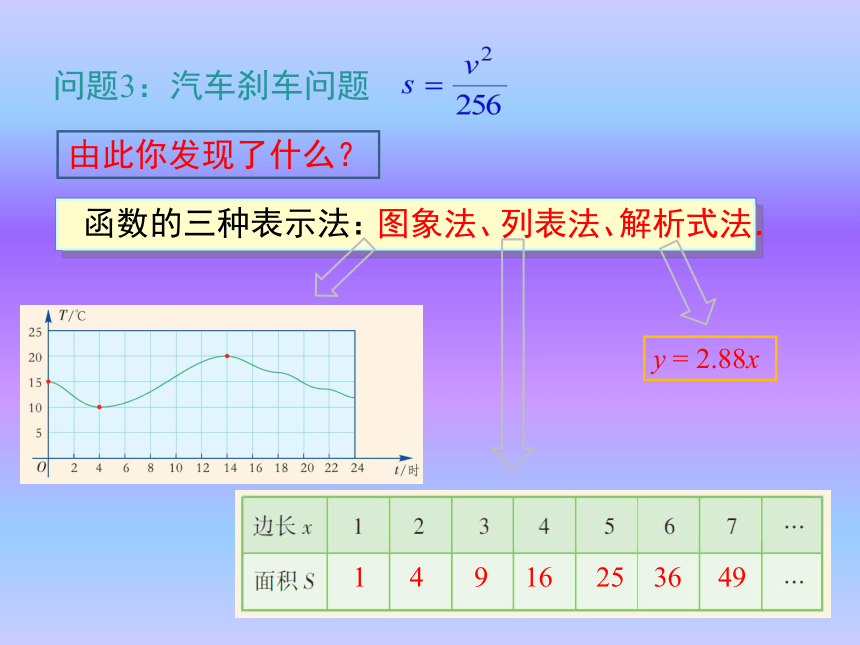
函数的三种表示法:y = 2.88x图象法、列表法、解析式法.问题3:汽车刹车问题由此你发现了什么?列表法解析法图象法定义实例优点通过列出自变量的值,与对应函数值的表格来表示函数关系的方法问题1具体反映了函数随自变量的数值对应关系用数学式子表示函数关系的方法问题3准确地反映了函数随自变量的数量关系用图象来表示两个
变量间的函数关系
的方法问题2直观地反映了函数随自变量的变化而变化的规律函数三种表示方法的区别例1 求下列函数中自变量x的取值范围:(1)y=2x+4; (2)y=-2x2;
(3) (4)解:(1)x为全体实数;
(2)x为全体实数;
(3)x≠2;
(4)x≥3.典例精析(1)解析式是整式时,自变量取全体实数;
(2)解析式是分式时,自变量的取值应使分母不为0;
(3)解析式是平方根时,自变量取值范围应使被开方数大于 或等于0;
(4)解决实际问题时,必须既符合理论又满足实际,特别注意:不要先化简关系式再求取值范围.解:(1)当x=3时,y=2x+4=2×3+4=10;
(2)当x=3时,y =-2x2=-2×32=-18;
(3)当x=3时,例2 当x=3时,求下列中函数的函数值:如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值. (4)当x=3时,(1)y=2x+4; (2)y =-2x2;
(3) (4)[归纳一]:函数关系式中自变量的取值范围一般主要考虑以下四种情况:
⑴函数关系式为整式形式:自变量取值范围为任意实数;
⑵函数关系式为分式形式:分母≠0;
⑶函数关系式含算术平方根:被开方数≥0;
⑷函数关系式含0指数:底数≠0.例3 一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.(1)写出游泳池内剩余水量Q m3与排水时间th间的函数关系式;(2)写出自变量t的取值范围.排水后的剩水量Q m3是排水时间h的函
数,有Q=-25 t +300. 池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t的取值范围是0≤t≤12.(3)开始排水后的第5h末,游泳池中还有多少水?(4)当游泳池中还剩150 m3水时,已经排水多长时间?当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3当Q=150m3时,由150=-25 t +300,得t =6h,
即第6 h末池中有水150m3.【归纳二】实际问题中自变量的取值范围.在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.例4 如何作出y=2x+1的图象?-3-1153 连线:作函数图象的一般步骤:列表、描点、连线.由函数表达式画图象的一般步骤:
1.列表:分析函数自变量的取值范围,取自变量的一些值(间隔相同),算出y的对应值;
2.描点:以表中对应值为坐标,在坐标系内描出相应的点;
3.连线:分析函数图象的发展趋势(是直线还是曲线,有限还是无限)按照自变量由小到大的顺序,用平滑的曲线连接所描的各点,即得图象.
注意:描出的点越多,图象就越精确. 例5 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米; (2)山顶离山脚的距离是300米,小强先爬上山; O(1)小强让爷爷先上多少米?(2)山顶高多少米?谁先爬上山顶?(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷; O(3)小强需多少时间追上爷爷?小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.O(4)谁的速度大?大多少?当堂练习1.求下列函数中自变量x的取值范围:x≠0x≠-1x≥0x为一切实数x≥2x为一切实数2.小明的爸爸早晨出去散步,从家走了20 min到达距离家800 m的公园,他在公园休息了10 min,然后用30 min原路返回家中,那么小明的爸爸离家的距离s(单位:m)与离家的时间t(单位: min)之间的函数关系图象大致是( )D 3.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:C 4.用解析式法与图象法表示等边三角形的周长l是边长a的函数.描点、连线:用描点法画函数l=3a的图象.O2xy123458641012 解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).5.一条小船沿直线向码头匀速前进.在0min ,2min,
4min,6min时,测得小船与码头的距离分别为200m,
150m,100m,50m.(1)小船与码头的距离是时间的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:是s = 200-25t船速度为(200-150)÷2=25m/min,
s=200-25t
t/min s/mO1234567 50100 150200画图:函数的表示方法列表法、解析法和图象法课堂小结自变量的取值范围使含自变量的等式有意义使实际问题有意义函数的表示方法——图象法函数的图象从函数的图象中获取信息画函数图象
2. 掌握函数自变量范围的确定和函数值的求法;
3. 能用这三种表示函数的方法解决简单的实际问题.(难点)学习目标导入新课回顾与思考下列问题中的变量y是不是x的函数?是(1) y = 2x(2) y+2x=3是不是(6)是(7) 不是(4) y=x2(5) y2=x(8) y=±x+5 (9) y=x2+3z是是不是不是(x≥0)在计算器上按照下面的程序进行操作:输入x(任意一个数)按键×2 = 显示y(计算结果)711-35207显示的数y是输入的数x的函数吗?为什么?填表:+5如果是,写出它的解析式.y = 2x+5导入新课动手操作讲授新课回想上一节课研究的三个问题问题1:用热气球探测高空气象问题2:绘制用电负荷曲线问题3:汽车刹车问题由此你发现了什么?表示函数
的一般方法列表法图象法解析法
函数的三种表示法:y = 2.88x图象法、列表法、解析式法.问题3:汽车刹车问题由此你发现了什么?列表法解析法图象法定义实例优点通过列出自变量的值,与对应函数值的表格来表示函数关系的方法问题1具体反映了函数随自变量的数值对应关系用数学式子表示函数关系的方法问题3准确地反映了函数随自变量的数量关系用图象来表示两个
变量间的函数关系
的方法问题2直观地反映了函数随自变量的变化而变化的规律函数三种表示方法的区别例1 求下列函数中自变量x的取值范围:(1)y=2x+4; (2)y=-2x2;
(3) (4)解:(1)x为全体实数;
(2)x为全体实数;
(3)x≠2;
(4)x≥3.典例精析(1)解析式是整式时,自变量取全体实数;
(2)解析式是分式时,自变量的取值应使分母不为0;
(3)解析式是平方根时,自变量取值范围应使被开方数大于 或等于0;
(4)解决实际问题时,必须既符合理论又满足实际,特别注意:不要先化简关系式再求取值范围.解:(1)当x=3时,y=2x+4=2×3+4=10;
(2)当x=3时,y =-2x2=-2×32=-18;
(3)当x=3时,例2 当x=3时,求下列中函数的函数值:如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值. (4)当x=3时,(1)y=2x+4; (2)y =-2x2;
(3) (4)[归纳一]:函数关系式中自变量的取值范围一般主要考虑以下四种情况:
⑴函数关系式为整式形式:自变量取值范围为任意实数;
⑵函数关系式为分式形式:分母≠0;
⑶函数关系式含算术平方根:被开方数≥0;
⑷函数关系式含0指数:底数≠0.例3 一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.(1)写出游泳池内剩余水量Q m3与排水时间th间的函数关系式;(2)写出自变量t的取值范围.排水后的剩水量Q m3是排水时间h的函
数,有Q=-25 t +300. 池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t的取值范围是0≤t≤12.(3)开始排水后的第5h末,游泳池中还有多少水?(4)当游泳池中还剩150 m3水时,已经排水多长时间?当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3当Q=150m3时,由150=-25 t +300,得t =6h,
即第6 h末池中有水150m3.【归纳二】实际问题中自变量的取值范围.在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.例4 如何作出y=2x+1的图象?-3-1153 连线:作函数图象的一般步骤:列表、描点、连线.由函数表达式画图象的一般步骤:
1.列表:分析函数自变量的取值范围,取自变量的一些值(间隔相同),算出y的对应值;
2.描点:以表中对应值为坐标,在坐标系内描出相应的点;
3.连线:分析函数图象的发展趋势(是直线还是曲线,有限还是无限)按照自变量由小到大的顺序,用平滑的曲线连接所描的各点,即得图象.
注意:描出的点越多,图象就越精确. 例5 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米; (2)山顶离山脚的距离是300米,小强先爬上山; O(1)小强让爷爷先上多少米?(2)山顶高多少米?谁先爬上山顶?(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷; O(3)小强需多少时间追上爷爷?小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.O(4)谁的速度大?大多少?当堂练习1.求下列函数中自变量x的取值范围:x≠0x≠-1x≥0x为一切实数x≥2x为一切实数2.小明的爸爸早晨出去散步,从家走了20 min到达距离家800 m的公园,他在公园休息了10 min,然后用30 min原路返回家中,那么小明的爸爸离家的距离s(单位:m)与离家的时间t(单位: min)之间的函数关系图象大致是( )D 3.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:C 4.用解析式法与图象法表示等边三角形的周长l是边长a的函数.描点、连线:用描点法画函数l=3a的图象.O2xy123458641012 解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).5.一条小船沿直线向码头匀速前进.在0min ,2min,
4min,6min时,测得小船与码头的距离分别为200m,
150m,100m,50m.(1)小船与码头的距离是时间的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:是s = 200-25t船速度为(200-150)÷2=25m/min,
s=200-25t
t/min s/mO1234567 50100 150200画图:函数的表示方法列表法、解析法和图象法课堂小结自变量的取值范围使含自变量的等式有意义使实际问题有意义函数的表示方法——图象法函数的图象从函数的图象中获取信息画函数图象
