人教版高中数学必修二教案:2.1.3空间中直线与平面之间的位置关系-2.1.4平面与平面之间的位置关系
文档属性
| 名称 | 人教版高中数学必修二教案:2.1.3空间中直线与平面之间的位置关系-2.1.4平面与平面之间的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 22:08:02 | ||
图片预览

文档简介
2.1.3 空间中直线与平面之间的位置关系~
2.1.4 平面与平面之间的位置关系
教学目标
1.了解直线与平面之间的三种位置关系,会用图形语言和符号语言表示.
2.了解平面与平面之间的两种位置关系,会用符号语言和图形语言表示.
教学重点:了解空间中直线与平面、平面与平面的位置关系
教学难点:会用图形语言、符号语言表示直线与平面、平面与平面之间的位置关系
教学过程
一、导入新课
情景1:飞机航线所在直线与地面有哪些位置关系呢?飞机双翅所在平面与地面有哪些位置关系呢?
情景2:围成长方体的六个面,两两之间的位置关系有几种?
我们今天就来学习: 2.1.3--2.1.4直线与平面、面面之间的关系.
二、新知探究与解题研究(认真阅读教材,完成下列各题)
(一)问题导学
问题1:一支笔所在的直线与一个作业本所在的平面,可能有几种位置关系?
【答案】三种位置关系
问题2:如图,线段A′B所在直线与长方体的六个面所在平面有几种位置关系?
【答案】三种位置关系:在面内,与平面相交,与平面平行
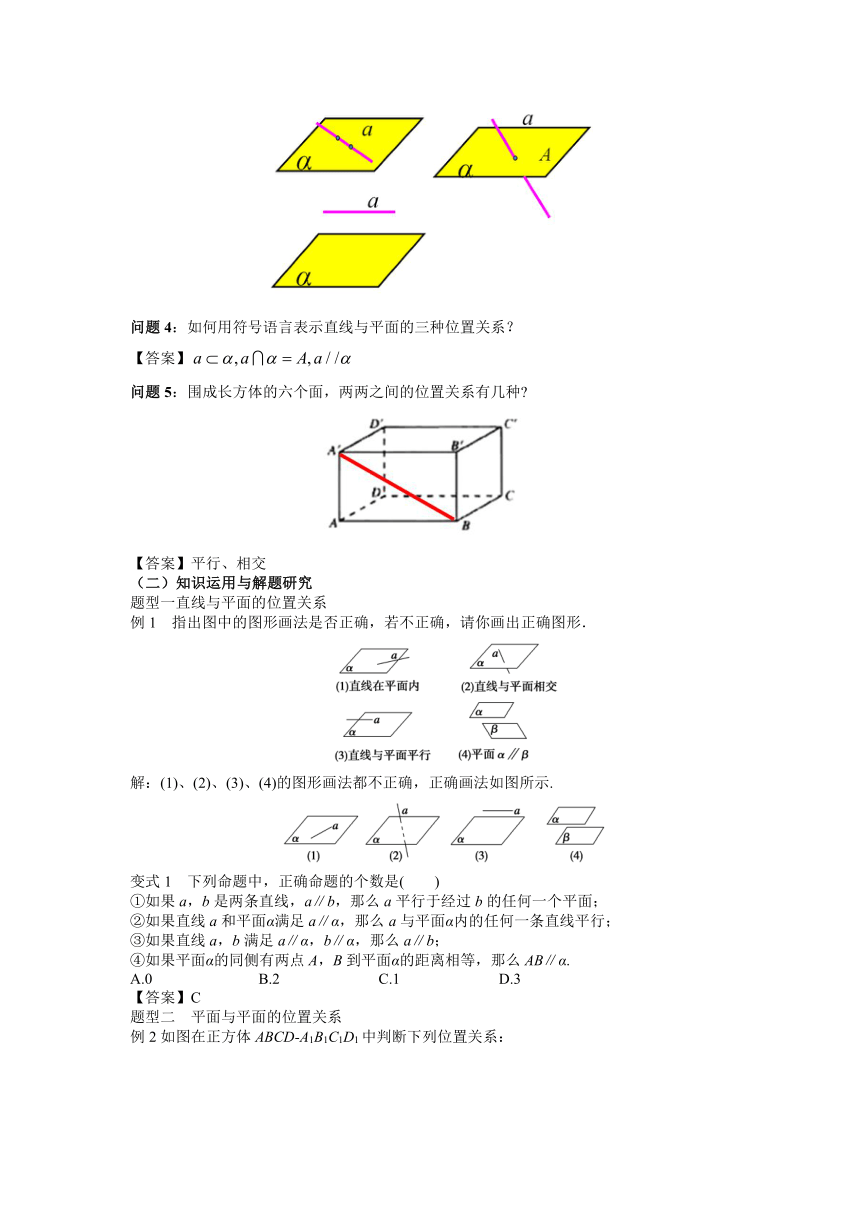
问题3:如何用图形语言表示直线与平面的三种位置关系?
【答案】如下图所示:
问题4:如何用符号语言表示直线与平面的三种位置关系?
【答案】
问题5:围成长方体的六个面,两两之间的位置关系有几种?
【答案】平行、相交
(二)知识运用与解题研究
题型一直线与平面的位置关系
例1 指出图中的图形画法是否正确,若不正确,请你画出正确图形.
解:(1)、(2)、(3)、(4)的图形画法都不正确,正确画法如图所示.
变式1 下列命题中,正确命题的个数是( )
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b满足a∥α,b∥α,那么a∥b;
④如果平面α的同侧有两点A,B到平面α的距离相等,那么AB∥α.
A.0 B.2 C.1 D.3
【答案】C
题型二 平面与平面的位置关系
例2如图在正方体ABCD- A1B1C1D1中判断下列位置关系:
(1)AD1所在直线与平面BCC1的位置关系是________;
(2)平面A1BC1与平面ABCD的位置关系是________.
【答案】(1)平行 (2)相交
变式2 以下四个命题中,正确的命题有( )
①在平面α内有两条直线和平面β平行,那么这两个平面平行;
②在平面α内有无数条直线和平面β平行,那么这两个平面平行;
③平面α内△ABC的三个顶点在平面β的同一侧面且到平面β的距离相等且不为0,那么这两个平面平行;
④平面α内两条相交直线和平面β内两条相交直线分别平行,那么这两个平面平行.
A.③④ B.②③④ C.②④ D.①④
【解析】当两个平面相交时,一个平面内有无数条直线平行于它们的交线,即平行另一个平面,所以①②错误.
【答案】A
类型三 平面与平面的位置关系的判断
例3以下说法中,正确的个数是( )
①平面α内有一条直线和平面β平行,那么这两个平面平行
②平面α内有两条直线和平面β平行,那么这两个平面平行
③平面α内有无数条直线和平面β平行,那么这两个平面平行
④平面α内任意一条直线和平面β都无公共点,那么这两个平面平行.
A.0个 B.1个 C.2个 D.3个
【解析】①平面α内有一条直线和平面β平行,那么这两个平面可能平行也可能相交;
②平面α内这两条直线平行时,此时这两个平面也可能相交;
③平面α内无数条直线都平行时,此时这两个平面也可能相交;
④显然正确.
【答案】B
点评:(1)由于下节课学习平面与平面的判定定理,所以现在判断两平面的位置关系或两平面内的线线,线面关系,我们常根据定义,借助实物模型“百宝箱”长方体(或正方体)进行判断.
(2)反证法也用于相关问题的证明.
变式3 (1)平面α内有无数条直线与平面β平行,问α∥β是否正确,为什么?
(2)平面α内的所有直线与平面β都平行,问α∥β是否正确,为什么?
解:(1)不正确.如图所示,设α∩β=l,则在平面α内与l平行的直线可以有无数条:a1,a2,…,an,…,它们是一组平行线,这时a1,a2,…,an,…与平面β都平行(因为a1,a2,…,an,…与平面β无交点),但此时α与β不平行,α∩β=l.
(2)正确.平面α内所有直线与平面β平行,则平面α与平面β无交点,符合平面与平面平行的定义.
三、当堂检测
1.如果直线a∥平面α,那么直线a与平面α内的( )
A.一条直线不相交 B.两条直线不相交
C.无数条直线不相交 D.任意一条直线不相交
【解析】直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.
【答案】D
2.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系为( )
A.平行 B.相交
C.直线在平面内 D.平行或直线在平面内
【解析】由面面平行的定义可知,若一条直线在两个平行平面的一个平面内,则这条直线与另一个平面无公共点,所以与另一个平面平行.由此可知,本题中这条直线可能在其中一个平面内.否则此直线与另一个平面平行(因为若一条直线与连个平行平面中的一个平面相交,则必然与另一个平面相交).
【答案】D
3. 下列命题中,正确命题的个数是()
①平行于同一条直线的两个平面平行;
②平行于同一个平面的两个平面平行;
③一个平面内有一条直线与另一平面平行,则这两个平面平行;
④两个平面平行,则分别在这两个平面内的两条直线平行.
A. 0 B. 1 C. 2 D. 3
【答案】B
课堂小结(引导学生总结本节课内容与方法)
1.直线与平面的位置关系:
①直线在平面内;
②直线与平面相交;
③直线与平面平行.
2.平面与平面的位置关系:
①平面与平面相交;
②平面与平面平行.
五、课后作业:课本练习题.
思考:下列命题:
①两个平面有无数个公共点,则这两个平面重合;
②若l,m是异面直线,l∥α,m∥β,则α∥β.
其中错误命题的序号为________.
【解析】对于①,两个平面相交,则有一条交线,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.
【答案】①②
2.1.4 平面与平面之间的位置关系
教学目标
1.了解直线与平面之间的三种位置关系,会用图形语言和符号语言表示.
2.了解平面与平面之间的两种位置关系,会用符号语言和图形语言表示.
教学重点:了解空间中直线与平面、平面与平面的位置关系
教学难点:会用图形语言、符号语言表示直线与平面、平面与平面之间的位置关系
教学过程
一、导入新课
情景1:飞机航线所在直线与地面有哪些位置关系呢?飞机双翅所在平面与地面有哪些位置关系呢?
情景2:围成长方体的六个面,两两之间的位置关系有几种?
我们今天就来学习: 2.1.3--2.1.4直线与平面、面面之间的关系.
二、新知探究与解题研究(认真阅读教材,完成下列各题)
(一)问题导学
问题1:一支笔所在的直线与一个作业本所在的平面,可能有几种位置关系?
【答案】三种位置关系
问题2:如图,线段A′B所在直线与长方体的六个面所在平面有几种位置关系?
【答案】三种位置关系:在面内,与平面相交,与平面平行
问题3:如何用图形语言表示直线与平面的三种位置关系?
【答案】如下图所示:
问题4:如何用符号语言表示直线与平面的三种位置关系?
【答案】
问题5:围成长方体的六个面,两两之间的位置关系有几种?
【答案】平行、相交
(二)知识运用与解题研究
题型一直线与平面的位置关系
例1 指出图中的图形画法是否正确,若不正确,请你画出正确图形.
解:(1)、(2)、(3)、(4)的图形画法都不正确,正确画法如图所示.
变式1 下列命题中,正确命题的个数是( )
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b满足a∥α,b∥α,那么a∥b;
④如果平面α的同侧有两点A,B到平面α的距离相等,那么AB∥α.
A.0 B.2 C.1 D.3
【答案】C
题型二 平面与平面的位置关系
例2如图在正方体ABCD- A1B1C1D1中判断下列位置关系:
(1)AD1所在直线与平面BCC1的位置关系是________;
(2)平面A1BC1与平面ABCD的位置关系是________.
【答案】(1)平行 (2)相交
变式2 以下四个命题中,正确的命题有( )
①在平面α内有两条直线和平面β平行,那么这两个平面平行;
②在平面α内有无数条直线和平面β平行,那么这两个平面平行;
③平面α内△ABC的三个顶点在平面β的同一侧面且到平面β的距离相等且不为0,那么这两个平面平行;
④平面α内两条相交直线和平面β内两条相交直线分别平行,那么这两个平面平行.
A.③④ B.②③④ C.②④ D.①④
【解析】当两个平面相交时,一个平面内有无数条直线平行于它们的交线,即平行另一个平面,所以①②错误.
【答案】A
类型三 平面与平面的位置关系的判断
例3以下说法中,正确的个数是( )
①平面α内有一条直线和平面β平行,那么这两个平面平行
②平面α内有两条直线和平面β平行,那么这两个平面平行
③平面α内有无数条直线和平面β平行,那么这两个平面平行
④平面α内任意一条直线和平面β都无公共点,那么这两个平面平行.
A.0个 B.1个 C.2个 D.3个
【解析】①平面α内有一条直线和平面β平行,那么这两个平面可能平行也可能相交;
②平面α内这两条直线平行时,此时这两个平面也可能相交;
③平面α内无数条直线都平行时,此时这两个平面也可能相交;
④显然正确.
【答案】B
点评:(1)由于下节课学习平面与平面的判定定理,所以现在判断两平面的位置关系或两平面内的线线,线面关系,我们常根据定义,借助实物模型“百宝箱”长方体(或正方体)进行判断.
(2)反证法也用于相关问题的证明.
变式3 (1)平面α内有无数条直线与平面β平行,问α∥β是否正确,为什么?
(2)平面α内的所有直线与平面β都平行,问α∥β是否正确,为什么?
解:(1)不正确.如图所示,设α∩β=l,则在平面α内与l平行的直线可以有无数条:a1,a2,…,an,…,它们是一组平行线,这时a1,a2,…,an,…与平面β都平行(因为a1,a2,…,an,…与平面β无交点),但此时α与β不平行,α∩β=l.
(2)正确.平面α内所有直线与平面β平行,则平面α与平面β无交点,符合平面与平面平行的定义.
三、当堂检测
1.如果直线a∥平面α,那么直线a与平面α内的( )
A.一条直线不相交 B.两条直线不相交
C.无数条直线不相交 D.任意一条直线不相交
【解析】直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.
【答案】D
2.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系为( )
A.平行 B.相交
C.直线在平面内 D.平行或直线在平面内
【解析】由面面平行的定义可知,若一条直线在两个平行平面的一个平面内,则这条直线与另一个平面无公共点,所以与另一个平面平行.由此可知,本题中这条直线可能在其中一个平面内.否则此直线与另一个平面平行(因为若一条直线与连个平行平面中的一个平面相交,则必然与另一个平面相交).
【答案】D
3. 下列命题中,正确命题的个数是()
①平行于同一条直线的两个平面平行;
②平行于同一个平面的两个平面平行;
③一个平面内有一条直线与另一平面平行,则这两个平面平行;
④两个平面平行,则分别在这两个平面内的两条直线平行.
A. 0 B. 1 C. 2 D. 3
【答案】B
课堂小结(引导学生总结本节课内容与方法)
1.直线与平面的位置关系:
①直线在平面内;
②直线与平面相交;
③直线与平面平行.
2.平面与平面的位置关系:
①平面与平面相交;
②平面与平面平行.
五、课后作业:课本练习题.
思考:下列命题:
①两个平面有无数个公共点,则这两个平面重合;
②若l,m是异面直线,l∥α,m∥β,则α∥β.
其中错误命题的序号为________.
【解析】对于①,两个平面相交,则有一条交线,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.
【答案】①②
