新高考湖北专用 第三章 直线与方程[必修2] 本章总结提升:26张PPT
文档属性
| 名称 | 新高考湖北专用 第三章 直线与方程[必修2] 本章总结提升:26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 00:00:00 | ||
图片预览








文档简介
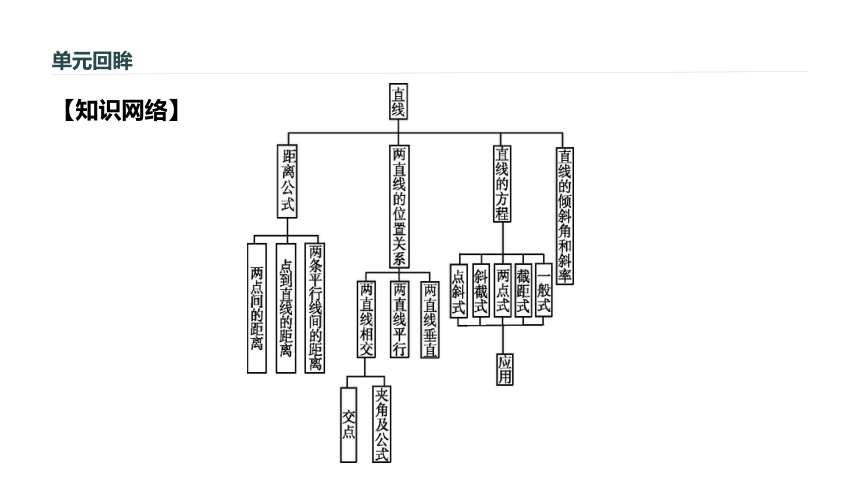
课件26张PPT。第三章 直线与方程[必修2]本章总结提升 单元回眸【知识网络】判断下列说法是否正确.(请在括号中填写“√”或“×”)
1.如果直线l1∥l2,那么l1的斜率等于l2的斜率,并且l1,l2与x轴交于相异的两点.( )
2.三条直线y+2x-4=0,x-y+1=0与ax-y+2=0共有两个交点,则a的值为-1或2.( )
单元回眸【知识辨析】××[解析] 由题意可得三条直线中有两条直线互相平行.∵直线x-y+1=0和直线y+2x-4=0不平行,∴直线x-y+1=0和直线ax-y+2=0平行或直线y+2x-4=0和直线ax-y+2=0平行.∵直线x-y+1=0的斜率为1,直线y+2x-4=0的斜率为-2,直线ax-y+2=0的斜率为a,∴a=1或a=-2.?3.若直线y=ax-2和y=(a+2)x+1互相垂直,则a=-1.( )
4.过点P(3,4)且在两坐标轴上的截距相等的直线的方程是x+y-7=0.( )单元回眸×√?5.过点(5,10),且与原点距离为5的直线方程只有3x-4y+25=0.( )××整合创新直线方程的基础知识题型一 [类型总述] (1)点斜式;(2)斜截式;(3)两点式;(4)截距式;(5)一般式.??整合创新例1 已知直线l在y轴上的截距为-1.
(2)若直线l在两个坐标轴上的截距相等,求直线l的方程.?整合创新??A整合创新变式 (2)过点P(6,8)作两条互相垂直的射线PA,PB,分别交x轴、y轴的正半轴于A,B两点.若S△AOB=S△APB,求PA与PB所在直线的方程.
?整合创新变式 (2)过点P(6,8)作两条互相垂直的射线PA,PB,分别交x轴、y轴的正半轴于A,B两点.若S△AOB=S△APB,求PA与PB所在直线的方程.
?整合创新直线的位置关系问题题型二例2 (1)经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程为 ( )
A.9x+18y-4=0
B.18x-9y-193=0
C.x+2y-4=0
D.2x-y-4=0
[类型总述] (1)平行;(2)垂直;(3)相交.A整合创新例2 (2)直线l1过点A(m,1)和点B(-1,m),直线l2过点C(m+n,n+1)和点D(n+1,n-m),则直线l1与l2的位置关系是( )
A.重合 B.平行 C.垂直 D.无法确定
?C整合创新变式 已知直线l1:x+y-1=0,将直线l1向上平移到直线l2的位置.若l1,l2和两坐标轴所围成的梯形的面积是4,求直线l2的方程.?整合创新距离问题题型三? [类型总述](1)点点距离;(2)点线距离;(3)线线距离.C?整合创新例3 (2)已知平行直线l1:2x+y-1=0,l2:2x+y+1=0,则l1与l2的距离是 .?
??整合创新?C?整合创新对称问题题型四? [类型总述](1)点点对称;(2)点线对称;(3)线点对称;(4)线线对称.A图T3-1整合创新例4 (2)平面直角坐标系中直线y=2x+1关于y=x-2对称的直线l的方程为 ( )
A.x-4y-11=0 B.4x-y+11=0 C.x-2y+7=0 D.x-2y-7=0
??整合创新例4 (2)平面直角坐标系中直线y=2x+1关于y=x-2对称的直线l的方程为 ( )
A.x-4y-11=0 B.4x-y+11=0 C.x-2y+7=0 D.x-2y-7=0
??整合创新例4 (3)若直线l1:y=kx+2-k与直线l2关于直线y=x-1对称,则直线l2恒过定点 .[解析] (3)∵直线l1:y=kx+2-k与直线l2关于直线y=x-1对称,∴直线l2的方程为x-1=k(y+1)+2-k,即x-ky-3=0,显然恒过定点(3,0).(3,0) 整合创新变式 已知直线l:y=3x+3.试求:
(1)点P(4,5)关于直线l对称的点的坐标;
?整合创新变式 已知直线l:y=3x+3.试求:(2)直线y=x-2关于直线l对称的直线的方程;
?整合创新变式 已知直线l:y=3x+3.试求:
(3)直线l关于点A(3,2)对称的直线的方程.
?整合创新最值问题题型五例5 (1)已知直线l1∥l2,A是l1,l2之间的一定点,并且A点到l1,l2的距离分别为1,2,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC的面积的最小值为( )
A.2 B.3
C.4 D.5[类型总述](1)三角形中边的性质;(2)二次函数最值.A整合创新?整合创新例5 (2)在平面直角坐标系xOy中,已知直线l:(2k-1)x+ky+1=0,则当实数k变化时,原点O到直线l的距离的最大值为 .???整合创新变式 设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|·|PB|的最大值是 .?
??
1.如果直线l1∥l2,那么l1的斜率等于l2的斜率,并且l1,l2与x轴交于相异的两点.( )
2.三条直线y+2x-4=0,x-y+1=0与ax-y+2=0共有两个交点,则a的值为-1或2.( )
单元回眸【知识辨析】××[解析] 由题意可得三条直线中有两条直线互相平行.∵直线x-y+1=0和直线y+2x-4=0不平行,∴直线x-y+1=0和直线ax-y+2=0平行或直线y+2x-4=0和直线ax-y+2=0平行.∵直线x-y+1=0的斜率为1,直线y+2x-4=0的斜率为-2,直线ax-y+2=0的斜率为a,∴a=1或a=-2.?3.若直线y=ax-2和y=(a+2)x+1互相垂直,则a=-1.( )
4.过点P(3,4)且在两坐标轴上的截距相等的直线的方程是x+y-7=0.( )单元回眸×√?5.过点(5,10),且与原点距离为5的直线方程只有3x-4y+25=0.( )××整合创新直线方程的基础知识题型一 [类型总述] (1)点斜式;(2)斜截式;(3)两点式;(4)截距式;(5)一般式.??整合创新例1 已知直线l在y轴上的截距为-1.
(2)若直线l在两个坐标轴上的截距相等,求直线l的方程.?整合创新??A整合创新变式 (2)过点P(6,8)作两条互相垂直的射线PA,PB,分别交x轴、y轴的正半轴于A,B两点.若S△AOB=S△APB,求PA与PB所在直线的方程.
?整合创新变式 (2)过点P(6,8)作两条互相垂直的射线PA,PB,分别交x轴、y轴的正半轴于A,B两点.若S△AOB=S△APB,求PA与PB所在直线的方程.
?整合创新直线的位置关系问题题型二例2 (1)经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程为 ( )
A.9x+18y-4=0
B.18x-9y-193=0
C.x+2y-4=0
D.2x-y-4=0
[类型总述] (1)平行;(2)垂直;(3)相交.A整合创新例2 (2)直线l1过点A(m,1)和点B(-1,m),直线l2过点C(m+n,n+1)和点D(n+1,n-m),则直线l1与l2的位置关系是( )
A.重合 B.平行 C.垂直 D.无法确定
?C整合创新变式 已知直线l1:x+y-1=0,将直线l1向上平移到直线l2的位置.若l1,l2和两坐标轴所围成的梯形的面积是4,求直线l2的方程.?整合创新距离问题题型三? [类型总述](1)点点距离;(2)点线距离;(3)线线距离.C?整合创新例3 (2)已知平行直线l1:2x+y-1=0,l2:2x+y+1=0,则l1与l2的距离是 .?
??整合创新?C?整合创新对称问题题型四? [类型总述](1)点点对称;(2)点线对称;(3)线点对称;(4)线线对称.A图T3-1整合创新例4 (2)平面直角坐标系中直线y=2x+1关于y=x-2对称的直线l的方程为 ( )
A.x-4y-11=0 B.4x-y+11=0 C.x-2y+7=0 D.x-2y-7=0
??整合创新例4 (2)平面直角坐标系中直线y=2x+1关于y=x-2对称的直线l的方程为 ( )
A.x-4y-11=0 B.4x-y+11=0 C.x-2y+7=0 D.x-2y-7=0
??整合创新例4 (3)若直线l1:y=kx+2-k与直线l2关于直线y=x-1对称,则直线l2恒过定点 .[解析] (3)∵直线l1:y=kx+2-k与直线l2关于直线y=x-1对称,∴直线l2的方程为x-1=k(y+1)+2-k,即x-ky-3=0,显然恒过定点(3,0).(3,0) 整合创新变式 已知直线l:y=3x+3.试求:
(1)点P(4,5)关于直线l对称的点的坐标;
?整合创新变式 已知直线l:y=3x+3.试求:(2)直线y=x-2关于直线l对称的直线的方程;
?整合创新变式 已知直线l:y=3x+3.试求:
(3)直线l关于点A(3,2)对称的直线的方程.
?整合创新最值问题题型五例5 (1)已知直线l1∥l2,A是l1,l2之间的一定点,并且A点到l1,l2的距离分别为1,2,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC的面积的最小值为( )
A.2 B.3
C.4 D.5[类型总述](1)三角形中边的性质;(2)二次函数最值.A整合创新?整合创新例5 (2)在平面直角坐标系xOy中,已知直线l:(2k-1)x+ky+1=0,则当实数k变化时,原点O到直线l的距离的最大值为 .???整合创新变式 设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|·|PB|的最大值是 .?
??
同课章节目录
