新高考湖北专用 第四章 圆与方程[必修2]本章总结提升:20张PPT
文档属性
| 名称 | 新高考湖北专用 第四章 圆与方程[必修2]本章总结提升:20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 00:00:00 | ||
图片预览

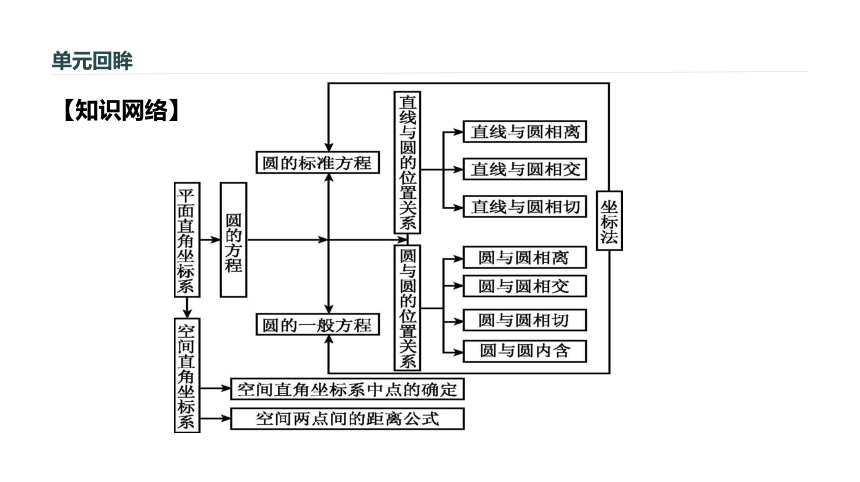







文档简介
课件20张PPT。第四章 圆与方程[必修2]本章总结提升 单元回眸【知识网络】?单元回眸【知识辨析】××[解析]因为点(1,2)在圆x2+(y-1)2=2上,因此过该点只能作1条该圆的切线.
√?单元回眸×?×整合创新圆的方程问题题型一[类型总述] (1)圆的标准方程;(2)圆的一般方程.??(x-2)2+y2=9整合创新例1 (2)已知a∈R,方程a2x2+(a+2)y2+4x+8y+5a=0表示圆,则圆心坐标是 ,半径是 .?(-2,-4)5整合创新变式 在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .??x2+y2-2x=0整合创新直线与圆、圆与圆的位置关系的应用题型二?[类型总述] (1)直线与圆的位置;(2)圆与圆的位置;(3)弦长公式;(4)垂径定理.B?整合创新??4整合创新变式 (1)y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .?
??整合创新??4π整合创新对称问题题型三?[类型总述] (1)点线对称;(2)直线与圆;(3)最值.4?整合创新例3 (2)圆C:x2+(y+1)2=4关于直线x+y-1=0对称的圆的方程是 .?
??整合创新变式 (1)若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为 .x2+(y-1)2=1[解析] (1)由圆C的圆心与点(1,0)关于直线y=x对称,得圆C的圆心为(0,1).又因为圆C的半径为1,所以圆C的标准方程为x2+(y-1)2=1.整合创新变式 (2)已知点P(a,b)关于直线l的对称点为P'(b,a),则圆C:x2+y2-4x-2y=0关于直线l对称的圆C'的标准方程为 .?
(x-1)2+(y-2)2=5?整合创新圆中的最值问题题型四? [类型总述] (1)圆系方程;(2)公共弦;(3)垂径定理.B(2)已知P是直线3x+4y+8=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线,A,B是切点,C是圆心,那么四边形PACB的面积的最小值为 .??整合创新???整合创新空间直角坐标系的应用题型五例5 如图T4-1所示,已知正方体ABCD - A1B1C1D1的棱长为1,点P是体对角线D1B的中点,点Q在棱CC1上,建立适当的空间直角坐标系.
(1)当2|CQ|=|QC1|时,求|PQ|的值;
(2)当Q在CC1上移动时,求|PQ|的最小值.[类型总述] (1)空间直角坐标系;(2)空间点的坐标;(3)空间两点间的距离公式.图T4-1整合创新?整合创新?
√?单元回眸×?×整合创新圆的方程问题题型一[类型总述] (1)圆的标准方程;(2)圆的一般方程.??(x-2)2+y2=9整合创新例1 (2)已知a∈R,方程a2x2+(a+2)y2+4x+8y+5a=0表示圆,则圆心坐标是 ,半径是 .?(-2,-4)5整合创新变式 在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .??x2+y2-2x=0整合创新直线与圆、圆与圆的位置关系的应用题型二?[类型总述] (1)直线与圆的位置;(2)圆与圆的位置;(3)弦长公式;(4)垂径定理.B?整合创新??4整合创新变式 (1)y=x+1与圆x2+y2+2y-3=0交于A,B两点,则|AB|= .?
??整合创新??4π整合创新对称问题题型三?[类型总述] (1)点线对称;(2)直线与圆;(3)最值.4?整合创新例3 (2)圆C:x2+(y+1)2=4关于直线x+y-1=0对称的圆的方程是 .?
??整合创新变式 (1)若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为 .x2+(y-1)2=1[解析] (1)由圆C的圆心与点(1,0)关于直线y=x对称,得圆C的圆心为(0,1).又因为圆C的半径为1,所以圆C的标准方程为x2+(y-1)2=1.整合创新变式 (2)已知点P(a,b)关于直线l的对称点为P'(b,a),则圆C:x2+y2-4x-2y=0关于直线l对称的圆C'的标准方程为 .?
(x-1)2+(y-2)2=5?整合创新圆中的最值问题题型四? [类型总述] (1)圆系方程;(2)公共弦;(3)垂径定理.B(2)已知P是直线3x+4y+8=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线,A,B是切点,C是圆心,那么四边形PACB的面积的最小值为 .??整合创新???整合创新空间直角坐标系的应用题型五例5 如图T4-1所示,已知正方体ABCD - A1B1C1D1的棱长为1,点P是体对角线D1B的中点,点Q在棱CC1上,建立适当的空间直角坐标系.
(1)当2|CQ|=|QC1|时,求|PQ|的值;
(2)当Q在CC1上移动时,求|PQ|的最小值.[类型总述] (1)空间直角坐标系;(2)空间点的坐标;(3)空间两点间的距离公式.图T4-1整合创新?整合创新?
同课章节目录
